Шушляков Д. А. 3 страница

Формулу (73) можно еще упростить.

Так как γh _c представляет собой гидростатическое давление в центре тяжести площади 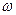, то справедливо равенство

Р = р_с ω. (74)

3.7. Давление жидкости на криволинейные поверхности. Закон Архимеда

Расположим оси координат 0 х и 0 у в плоскости свободной поверхности жидкости, а ось 0zнаправим вертикально вниз (рис. 11). Допустим, что внутри жидкости расположена жесткая, непроницаемая криволинейная пластинка, не имеющая толщины (толщина 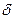=0) и к тому же невесомая. Очевидно, такая пластинка будет неподвижной. Требуется определить, с какой силой жидкость давит на эту пластинку.

Пусть на верхнюю сторону пластинки жидкость оказывает давление с силой R, а на нижнюю — силой R'. Эти силы по величине равны между собой, действуют по одной прямой и противоположно одна другой по направлению, так что безразлично, какую из них мы будем определять. Найдем, например, силу R, равнодействующую элементарных сил dP.

Так как поверхность пластинки криволинейна, то силы dP образуют систему непараллельных сил. Такая система в общем случае приводится к главному вектору и одной паре сил. Разложим каждую элементарную силу dP на три составляющие по координатным осям, т. е. на dP_x, dP_y и dP_z. Очевидно,

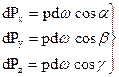; (75)

где α, 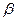, и γ — углы наклона элементарных сил dp к координатным осям, различные для разных площадок dω.

Суммируя проекции элементарных сил, найдем соответствующие проекции равнодействующей силы R:

R_x = Σ pd ωcos α;

Ry = Σ pd ω cosβ;

Rz = Σ pd ω cos γ.

Сила R по величине будет равна:

,

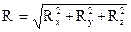а направление линии ее действия найдем по направляющим косинусам:

cos 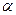= 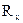/R, cos 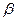= 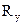/R, cos 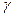= 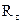/R.

Понятно, что указанный здесь способ решения осложняется или даже становится невозможным, если поверхность S не может быть выражена алгебраически в виде функции S (x, у, z). Упростим это решение.

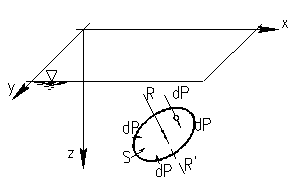
Рис. 11 – Давление жидкости на криволинейную стенку

Систему уравнений (75) можно записать так:

dR_x = pd ωcos α = pd ω _x;

dR_y = pd ωcos β= pd ω _y;

dR_z = pd ωcos γ= pd ω _z,

где d ω _x – проекция площадки dω на любую вертикальную плоскость, перпендикулярную оси 0 х (в частности, например, на плоскость y0 z); аналогично 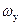d и d 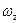- суть проекции площадки dω на плоскости, перпендикулярные осям 0 у и 0 z.

Выражение pd ω _x представляет собой силу давления жидкости на элементарную площадку d ω _x (рис. 12).

Рис. 12 – Давление жидкости на криволинейную поверхность по горизонтальному направлению

Интегрируя, получим

.

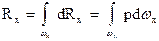Но интеграл 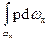представляет собой силу давления жидкости на всю плоскую площадку 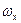(см. рис. 12), поэтому 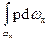= 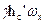,где h'_c — глубина погружения центра тяжести площади 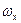под уровень свободной поверхности. Итак, получим силу

Rx = Px = γh́cωx

По аналогии

Ry = Py = γh˝cωy

Таким образом, проекции на горизонтальные оси силы давления жидкости R на криволинейную поверхность (ABCDA на рис. 12) равны силам давления на проекции ωx (A'B'D'C' на рис. 12) и ω _у этой поверхности на вертикальные плоскости, соответственно перпендикулярные осям. Определим теперь вертикальную проекцию силы R, т. е. силу R_z. Последняя, очевидно, равна:

.

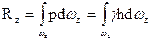где h – глубина погружения площадки dω под уровень свободной поверхности (рис. 13). Произведение hd ω _z можно рассматривать как элементарный объем dW. Поэтому силу R_z можно выразить как

,

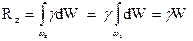где W – объем вертикального цилиндра (ABCDA'B'C'D'). Следовательно, сила R_z равна весу жидкости в объеме вертикального столба, опирающегося на заданную криволинейную поверхность и ограниченного плоскостью свободной поверхности.

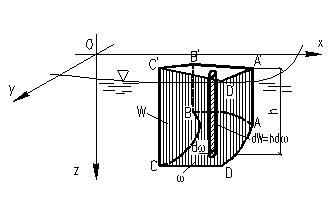
Рис. 13 – Давление жидкости на криволинейную стенку по вертикальному направлению

Пусть цилиндрический напорный резервуар снабжен съемной цилиндрической крышкой АВ, длина которой вдоль образующей резервуара равна единице (рис. 14). Определить силу R давления жидкости на эту крышку.

Из предыдущего

.

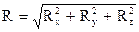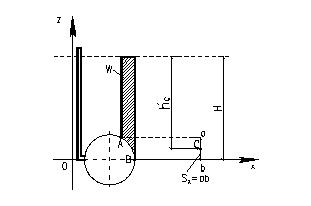
Рис. 14 – К определению силы давления

При указанном на рис. 14 расположении осей сила R_y = 0, а сила R_x = =yh́_cS_x (где S_x — проекция крышки АВ на плоскость zoy имеет форму прямоугольника).

Глубина погружения центра тяжести этой площади (точки с)

,

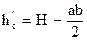Откуда

.

Вертикальная составляющая R_z находится по формуле

R 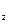= γW,

где объем W показан штриховкой на рис. 14 (этот объем всегда можно вычислить с той или иной степенью точности).

Линия действия полной силы давления R пересекает ось цилиндра под углом наклона к горизонту α, величина которого определяется из условия tgα = .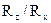

Закон Архимеда. Определим давление жидкости на погруженное в него тело (рис. 15).

При изображенном на рис. 15 расположении координатных осей компоненты 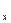R и R равны нулю и сила давления на всю поверхность погруженного тела

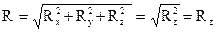
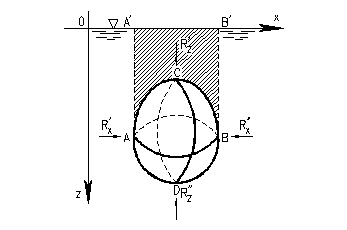
Рис. 15 – К закону Архимеда

Определим значение R_z. Проведя контурную линию АВ (смотря на тело сверху), разделим поверхность тела на две части — верхнюю и нижнюю. На верхнюю часть поверхности жидкость давит с силой R'_z, а на нижнюю — с силой R˝z, причем

R 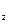= R'_z - R˝z

где

R_z = γW(AÁ В́ ВСА), a R˝z = γW (AÁ B́BDA),

Тогда

R 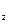= R'_z — R˝z= γ [ W (AÁ B́ BCA) — W (AÁ B́ BDA)] = — yW (AC BDA),

или короче

R = -γW (76)

где W —объем тела.

Таким образом, по закону Архимеда сила, с которой жидкость действует на погруженное в нее тело, равна весу жидкости в объеме погруженного тела. Эта сила называется Архимедовой подъемной силой.

4. Уравнение энергии и теорема импульсов

4.1. Основные понятия и определения движения жидкости

Движение жидкостей может быть разделено на установившееся и неустановившееся.

Движение называется установившимся, если все характеристики движения в одной и той же точке пространства (в том числе их скорость) не меняются во времени.

Движение, не удовлетворяющее этому определению, называется неустановившимся.

Примером установившегося движения может служить истечение жидкости из отверстия в стенке резервуара под постоянным напором (Н= const) или истечение газа из отверстия замкнутого резервуара, давление и температура в котором поддерживаются неизменными.

Примером неустановившегося движения является опорожнение резервуара при переменных значениях напора или давления.

В настоящей главе мы рассмотрим законы только установившегося движения. Но и в этом случае движение жидкости как сплошной, легко деформируемой среды представляет собой сложный физический процесс, точное математическое описание которого связано с чрезвычайными трудностями.

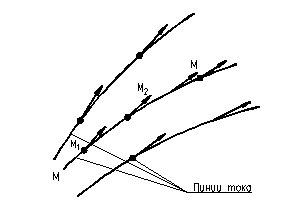
Рис. 16 – Линии тока

Поэтому для облегчения теоретических решений обычно вводятся различные схемы и модели, заменяющие реальный поток жидкости. Важным является понятие о струйчатой структуре течения жидкости, в соответствии с которым поток представляется как совокупность элементарных струек, вплотную прилегающих друг к другу и образующих сплошную массу движущейся жидкости.

Изучив законы движения элементарной струйки, легче установить основные законы движения всего потока в целом.

Линия тока и элементарная струйка. Линией тока называется линия, проходящая через последовательно движущиеся одна за другой частицы жидкости, векторы скоростей которых направлены по касательным к этой линии М - М (рис. 16). Линия тока и траектория движения частицы в общем случае (т. е. при неустановившемся движении) не совпадают одна с другой, но совпадают при установившемся движении. Это положение удобно иллюстрировать на примере, изображенном на рис. 17. Здесь при истечении жидкости из отверстия резервуара вытекающая струя непрерывно меняет свое положение во времени. На рисунке даны три положения струи соответственно для трех моментов времени t1, t₂ и t3 для которых условно изображены три линии тока 1, и, кроме того, отмечены три положения частицы М для тех же моментов времени и пунктиром указана траектория 2 этой частицы.

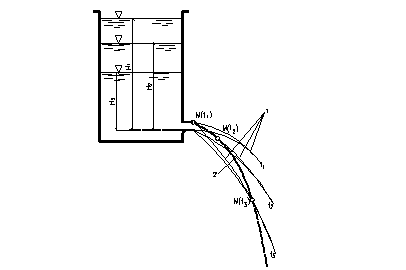
Рис. 17 – Линии тока, не совпадающие с траекториями при

неустановившемся движении

Две различные линии тока не пересекаются между собой.

Элементарной струйкой называется струйка, боковая поверхность которой образована линиями тока, проходящими через точки очень малого (в пределе – бесконечно малого) замкнутого контура. Таким образом, эта струйка оказывается изолированной от окружающей ее массы жидкости и имеет малую площадь поперечного сечения ∆ω (в пределе dω), которая может меняться по длине. Длина этой струйки неограниченна. Боковая поверхность струйки непроницаема для жидкости, т. е. ее можно представить в виде трубки, внутри которой течет жидкость.

Основные виды движения. Расход жидкости. Движение может быть равномерным и неравномерным, сплошным и прерывистым. При равномерном движении величина скорости не меняется по длине струйки, в противном случае движение называется неравномерным.

Обратимся к понятию о расходе жидкости.

Пусть в некотором поперечном сечении элементарной струйки скорость равна и.За время dtчастицы жидкости переместятся на расстояние ds = udt.Следующие за ними частицы жидкости заполнят все освобождаемое пространство, и поэтому за указанное время dtчерез поперечное сечение пройдет объем жидкости

dW=dsdω=udωdt

Объем жидкости, протекающей через сечение за единицу времени, называют объемным расходом жидкости. Обозначая расход элементарной струйки через dQ, получим для него выражение

dQ=udω (77)

Рассмотрим такое движение жидкости, при котором в потоке не возникает пустот (т. е. текущая жидкость представляется сплошной средой). В этом случае для двух соседних сечений элементарной струйки несжимаемой жидкости I и II (на рис. 18) можем написать

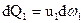
и аналогично

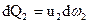
По условию сплошности течения dQ₁не может быть меньше dQ₂, иначе между сечениями I и II образовалась бы пустота, так как в этом случае из сечения II выходило бы большее количество жидкости, чем входит через сечение I. Точно так же dQ₁не может быть больше dQ₂. Следовательно, единственно возможное условие: dQ₁ = dQ₂. Повторяя эти рассуждения применительно к другим сечениям струйки, можем написать

dQ₁ = dQ₂ =… = dQ_n = dQ, (78)

или

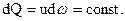(79)

Таким образом, объемный расход жидкости остается неизменным на всем протяжении данной элементарной струйки. В случае сжимаемой (газообразной) жидкости требование сплошности приводит к установлению равенства между собой количества массы жидкости, протекающей через соседние сечения (массового расхода), или равенства весового расхода, т. е.

dQ 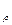=ρudω

или

dQ 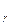=γudω

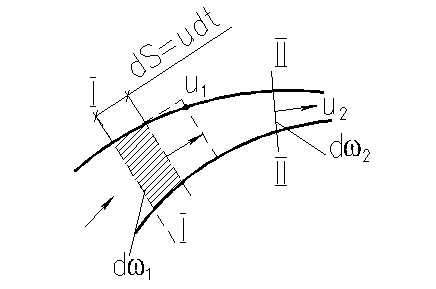
Рис. 18 – Элементарная струйка тока

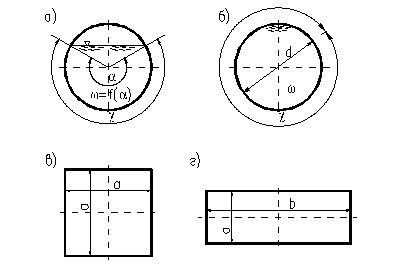
Рис. 19 – К определению площади поперечного сечения

Расход потока жидкости равен алгебраической сумме расходов элементарных струек, составляющих данный поток.

Скорость жидкости в различных точках поперечного сечения потока, так называемая местная скорость, очевидно, может быть неодинаковой, поэтому для характеристики движения всего потока вводится в рассмотрение средняя по всему сечению скорость потока. Средняя скорость определяется выражением

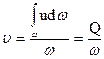, (80)

из которого следует, что расход потока жидкости равен средней скорости, умноженной на площадь его поперечного сечения:

Q= 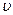ω.

В связи с этим условие сплошности потока (или неразрывности течения) для несжимаемой жидкости можно записать в виде

Q = 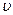ω = const. (81)

Для газообразной жидкости; обозначая через Qρ массовый и через Qγ весовой расходы, имеем

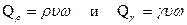, (82)

и тогда условие сплошности приобретает следующий вид:

.

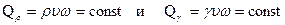В гидравлических расчетах для характеристики размеров и формы поперечного сечения потока вводятся понятия о живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.

Живым сечением называют часть поперечного сечения канала, заполненную жидкостью. Так, в круглой трубе диаметром d (рис.19, a) живое сечение потока меньше площади круга, если не все сечение трубы заполнено жидкостью, тогда как для случая, когда все поперечное сечение занято жидкостью, живым сечением является площадь круга πd²/4 (рис. 19, б).

Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками канала (трубы). Смоченный периметр обозначают обычно греческой буквой χ. Если, например, все сечение трубы занято жидкостью (т. е. живое сечение ω = πd²/4), то смоченный периметр равен длине окружности: χ =πd

Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т. е. величину

.

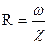В частности, для круглых труб, заполненных жидкостью, гидравлический радиус равен четверти диаметра. Действительно

.

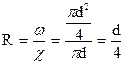В отопительной и вентиляционной практике широко пользуются понятием об «эквивалентном диаметре», который определяют по формуле

.

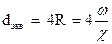Очевидно, что эквивалентный диаметр, равный четырем гидравлическим радиусам, для круглого сечения (рис. 19, б) равен диаметру трубы:

.

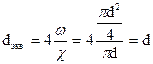для квадратного сечения (рис. 19, в)

,

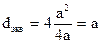т. е. равен стороне квадрата, а для прямоугольного сечения (рис. 19,г)

.

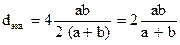Приведенные здесь основные понятия позволяют решать различные практические задачи.

4.2. Уравнение Бернулли для элементарной струйки несжимаемой жидкости

Выделим в элементарной струйке (рис. 20) сечениями I и II некоторую массу жидкости и составим уравнение кинетической энергии для этой массы. (Как известно, приращение кинетической энергии выделенной массы равно работе внешних сил на данном перемещении).

За время dtвыделенная масса, переместившись, займет положение, ограниченное сечениями I'—II'. Область между этими сечениями можно разделить на три объема: а, bи с;при этом по условию сплошности масса объема а равняется массе объема b.

Приращение кинетической энергии ∆m 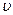²/2при перемещении выделенной массы жидкости из положения I—II в положение I'—II'

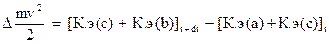. (83)

Так как движение установившееся, то кинетическая энергия жидкости объема с в моменты t и t+dtбудет неизменной,

Поэтому для всей выделенной массы

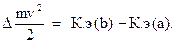(84)

Определим величину кинетической энергии жидкости в объёме b

.

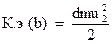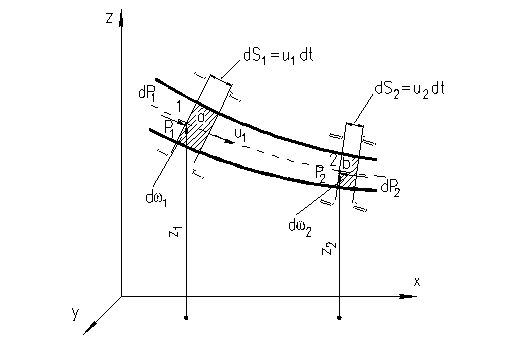
Рис. 20 – К выводу уравнения Бернулли

Но

,

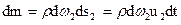откуда

,

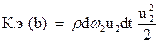и аналогично

.

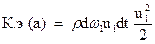Приращение кинетической энергии рассматриваемой массы жидкости

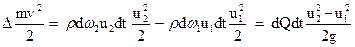, (85)

где dQ – массовый расход, одинаковый независимо от рассматриваемого сечения.

В случае невязкой жидкости к выделенному объему приложены силы тяжести, сила давления жидкости на боковую поверхность и силы давления на торцовые площадки объема.

Поскольку жидкость несжимаема, внутренняя энергия рассматриваемого объема не меняется при его перемещении, и в уравнение кинетической энергии входит только работа внешних сил. При перемещении выделенной массы жидкости из положения I - II в положение I' - II' вес жидкости в объеме сработу не совершает, и, следовательно, работа сил тяжести может быть вычислена как работа при перемещении жидкости, заключенной в объеме а, в положение жидкости, заключенной в объеме b:

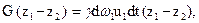
где z₁и z₂ — расстояния до центров тяжести объемов а и b от некоторой горизонтальной плоскости или, иначе, ордината этих центров тяжести. Можно также рассматривать 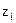и z₂ с точностью до малых высшего порядка как ординаты центров сечений I и II.

Работа сил давления на боковую поверхность выделенного объема равняется нулю, так как эти силы нормальны к этой поверхности. Работа сил давления на торцы равна разности

.

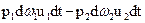Уравнение кинетической энергии имеет, таким образом, следующий вид:

.

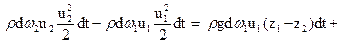
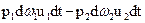Разделим на dtи сгруппируем члены этого уравнения, помещая члены, относящиеся к сечению I, в левую часть, а относящиеся к сечению I – в правую часть равенства. В результате получим:

.

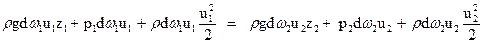Заменив u₁dω₁= u₂dω₂=dQ, и разделив затем левую и правую части на величину pgdQ,получим

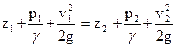, (86)

где ρg=γ

Это и есть уравнение Бернулли, написанное для участка элементарной струйки между сечениями I и II. Его можно представить также в разностной форме:

,

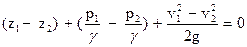или, обозначая разности между величинами в скобках в виде приращений,

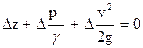, (87)

Если неограниченно сближать между собой сечения I и II, то уравнение (87) можно представить в дифференциальной форме:

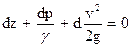, (88)

Так как сечения I и II взяты произвольно, то уравнение Бернулли можно записать также в виде

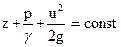, (89)

Геометрическое и энергетическое истолкование уравнения Бернулли. Рассмотрим сначала геометрическое истолкование.

Отнесем струйку к системе координат xyz (рис. 21) и напишем уравнение Бернулли для трех произвольных сечений струйки:

.

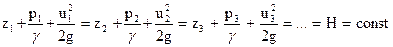Здесь z- геометрическая высота центра тяжести сечения над плоскостью х0у;

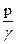– пьезометрическая высота;

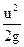- скоростная высота или скоростной напор.

Все эти величины имеют линейную размерность, следовательно, их сумма, обозначаемая через H, имеет также размерность длины. Величину H называют полным напором в данном сечении струйки.

Для каждого поперечного сечения элементарной струйки величина H может быть представлена совокупностью отрезков z, 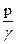и 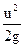как это изображено на рис. 21.

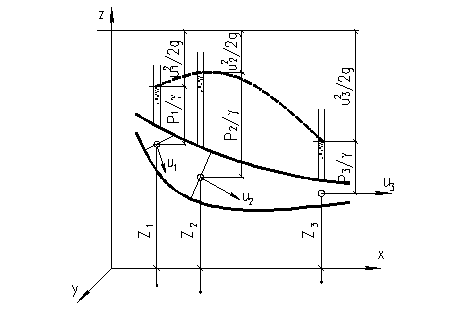
Рис. 21 – Пьезометрическая кривая

Соединив между собой концы отрезков H, получим кривую, расположенную в горизонтальной плоскости; эту плоскость и кривую на ней называют плоскостью и линией полного напора.

Соединив кривой концы отрезков 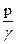, получим линию, которую называют пьезометрической линией или пьезометрической кривой.

Итак, рис. 21 дает геометрическое истолкование уравнения Бернулли. Можно видеть, как по длине струйки меняются слагаемые этого уравнения. Если сечение расширяется и, следовательно, скорость уменьшается, то уменьшается скоростной напор, но возрастает сумма .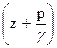

Если рассматривать уравнение Бернулли как уравнение энергии, то каждое слагаемое этого уравнения надо расценивать как некоторую составляющую полной энергии (потенциальную или кинетическую), и каждое из этих слагаемых должно измеряться в единицах работы. Уравнение (89) представлено в линейных единицах, поэтому, чтобы перевести его в уравнение работы, надо помножить его на единицу силы; если помножить его, например, на 1 Н, то уравнение не изменится, но размерность каждого слагаемого будет выражена в Н·м (Дж) и, следовательно, представит собой некоторую энергию, отнесенную к 1 Н жидкости, проходящей через данное сечение в 1 с. Такую энергию называют удельной. В соответствии с этим z будет удельной потенциальной энергией, обусловленной тем, что данный 1 Н жидкости находится на высоте z (относительно плоскости у0х)и может совершать работу, равную z, Дж.

Аналогично 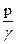будет удельной потенциальной энергией, зависящей от давления р. Таким образом, тот же 1 Н жидкости, находящейся на высоте z, обладает еще энергией давления, равной 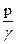Дж. Итак, 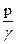- потенциальная удельная энергия давления.

Величина 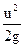зависит от скорости, следовательно, это будет удельная кинетическая энергия.

Пьезометрическая линия отделяет область изменения потенциальной энергии от области изменения кинетической энергии.

Легко видеть, что с энергетической точки зрения уравнение Бернулли показывает, что сумма потенциальной энергии (положения и давления) и кинетической энергии есть величина постоянная, т. е. одинаковая по пути данной элементарной струйки невязкой жидкости. Полная удельная энергия остается неизменной. Таким образом, уравнение Бернулли представляет закон сохранения механической энергии при движении идеальной жидкости.

Уравнение Бернулли для элементарной струйки вязкой жидкости. Вязкая жидкость испытывает сопротивление при движении, и ее удельная энергия не может сохраняться неизменной вдоль струйки.

В соответствии с этим при движении вязкой жидкости в уравнение Бернулли надо ввести поправку на потери напора при ходе от некоторого сечения струйки к сечению, расположенному ниже по течению. Обозначая потери напора через ∆h_ω, получимследующую запись уравнения Бернулли применительно к некоторым двум произвольным сечениям струйки жидкости:

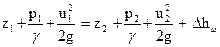(90)

или

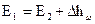
Дата добавления: 2014-12-26