Модельное время и виды процессов

Ключевые слова: модельное время, процесс, дискретный (прерывный) процесс, аналоговый (непрерывный) процесс, шаг моделирования, диапазон (интервал моделирования, просчёт модели, аппроксимация, предобработка)

Просчёт любой модели предполагает обработку данных во времени. Следовательно, в выражении (1) присутствует время, которое выражено через изменение значений вектора параметров X. Это позволяет рассматривать все параметры системы в динамике. Но соответствует ли модельное время тому времени, которое рассматривается в физике? Практика показывает, что это происходит далеко не всегда, поэтому обратимся к определению.

& Модельное время (англ. model time) – критерий моделируемого объекта, имеющий однонаправленную динамику (возрастание или снижение), относительно изменения которого оцениваются остальные показатели исследуемой модели.

В качестве модельного времени показатель физического времени необязателен: динамику модели можно отслеживать относительно изменения любого удовлетворяющего определению показателя. Например, шкалой модельного времени может являться ценовой диапазон, для исследования поведения модели в котором последовательно рассчитываются другие критерии.

Таким образом, модельное время следует отличать от реального времени – исторической шкалы моделируемого объекта. Ещё одним понятием является машинное время, отражающее период времени, затрачиваемый ЭВМ на один полный просчёт модели.

Теперь следует рассмотреть свойства, которыми характеризуется модельное время. Рационально выделить четыре основные характеристики: это шкала моделирования (масштаб), шаг моделирования, диапазон моделирования и вид модельного времени. Рассмотрим их подробнее.

Шкала моделирования определяется той величиной, которая была взята в качестве базовой, то есть в качестве модельного времени. От этого зависит масштаб рассмотрения процессов, моделируемых в системе. Следовательно, от детализации, то есть от минимального деления шкалы времени моделирования, будет зависеть, в каких единицах измерения будут заданы шаг и диапазон моделирования.

Важным элементом модели является такой параметр, как шаг моделирования.

& Шаг моделирования (англ. step of calculation model) – совокупность действий, происходящих в единицу модельного времени и характеризующие очередной этап просчёта модели.

От того, какой длины будет выбран шаг моделирования, будет зависеть детальность и частота просчёта модели. Например, если моделируется значение курса акции предприятия на бирже с интервалом в 1 час, то можно получить довольно гладкую кривую, описывающую колебание её курса. Если же в качестве шага выбрать одну минуту, то можно получить сложную динамику, ярко демонстрирующую вклад случайных процессов (шумов) на результаты работы модели. Традиционно шаг моделирования выбирается константой, хотя существуют модели, в которых это правило сознательно нарушается. В данном пособии шаг моделирования везде будет считаться постоянным.

Для просчёта модели мало определить то, с какой частотой будет вестись прогон. Для корректного описания ситуации требуется знать интервал моделирования.

& Диапазон (интервал) моделирования (англ. interval of calculation model) – интервал шкалы модельного времени, на котором будет просчитана модель с частотой, равной шагу моделирования.

Очевидно, что диапазон моделирования можно задать двумя способами: первый – указать начальное и конечное значения на шкале модельного времени (например, работа завода в течение смены, то есть с 8:00 до 17:00, с учётом обеденного перерыва); и второе – отметить начальное значении, а затем указать длительность моделирования в терминах шкалы моделирования (например, начиная с 8:00 и далее 8 часов).

Рассмотрев модельное время, следует обратиться к вопросу описания процессов в моделях. Любые процессы в моделируемой системе относительно модельного времени можно разделить на два типа: аналоговые и дискретные. Дадим их определения:

& Аналоговый процесс (англ. analog process) – процесс, регистрируемый в виде непрерывного потока значений, постепенно переходящих от одного значения к другому.

& Дискретный процесс (англ. discreed process) – процесс, регистрируемый в виде последовательности отдельных значений, не позволяющих сделать однозначное заключение о характере перехода между соседними значениями.

Если известны все взаимодействия частей системы в виде формальных законов (обычно это уравнения), то модель строится на основе аналоговых процессов, имеющих непрерывную природу. Примером таких процессов могут быть значения, отражающие динамику высоты полёта метеозонда, температуры котла с расплавом стали, рыночного спроса на холодильники и пр. Аналоговые процессы изображаются непрерывной кривой или последовательностью точек, которые можно соединить отрезками (интерполировать) или огибающей кривой (аппроксимировать). Пример представлен на рис. 3, а. Запись аналоговой закономерности в виде уравнений называется аналитическим представлением.

а	б

Рис. 3. Пример изображения аналогового и дискретного процессов

В других ситуациях, когда нет исчерпывающей информации о моделируемом объекте, известны отдельные ряды значений интересующих исследователя показателей. Формул ещё нет, и поэтому значения представлены в виде последовательности точек, то есть как дискретный процесс. Например, временные ряды замечательно отражают динамику цен на товар в супермаркете, режимы работы оборудования в цехе, статистику операций на бирже и пр. Дискретные процессы изображаются в виде последовательности точек либо как гистограмма или ступенчатый график (рис. 3, б): в их значениях отражены отдельные состояния моделируемого процесса, переходы между которыми скачкообразны. Запись дискретной закономерности в виде временного ряда ещё называется эмпирическим представлением.

Просчёт модели в среде моделирования осуществляется равномерными шагами (квантуется). При этом нет разницы, задаются процессы в модели аналоговым законом (гладкой кривой) или дискретным (ломаная ступенчатая линия). Очевидно, что при ширине шага моделирования, стремящейся к нулю, динамика системы будет носить плавный, подробный, постепенный характер, а при значительной ширине – разрозненные, скачкообразные значения. Исходя из данной закономерности, всегда можно перейти от дискретного процесса к аналоговому и наоборот. Для получения отдельных значений процесса, описываемого дифференциальным законом, достаточно подставить в его уравнение значения модельного времени.

Из этого можно сделать вывод: важен не тип процессов, используемый в модели, а умение с ним правильно обращаться. Тогда возникает вопрос: при каких обстоятельствах рационально использовать тот или иной тип описания процесса? Выбор типа представления динамики процесса зависит от конкретной задачи и исходных данных. Каждый из них обладает как положительными, так и отрицательными чертами (табл. 1). Поэтому там, где не требуется результат повышенной точности, рационально переходить от одного типа к другому и обратно в соответствии с потребностями задачи и удобством работы.

В процессе работы с моделью нередко возникает такая ситуация, что отдельные ряды данных не могут быть корректно использованы для просчёта модели. Это связано с тем, что интервалы между значениями ряда могут быть неравномерны или иметь частоту, не совпадающую с шагом моделирования.

Например, концентрацию потока вещества (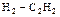) при синтезе углеродных нанотрубок на кремниевой подложке замеряли в первую, пятую, седьмую, двенадцатую и семнадцатую минуты процесса. Если шаг моделирования выбран равным 4, а интервал моделирования ограничен первой и семнадцатой минутой, то требуется пересчёт исходных значений для нового ряда (первая, пятая, девятая, тринадцатая, семнадцатая минуты соответственно), который носит название предобработки.

Таблица 1

Характеристика типов процессов

Тип процесса	Достоинства	Недостатки
Аналитическое представление (уравнение)	– детальное отражение динамики; – получение значений в любой точке; – быстрая реакция системы на управляющий сигнал	– необходимость учёта всех влияющих факторов; – требуются большие вычислительные мощности
Эмпирическое представление (дискретные данные)	– выявляют скрытые закономерности между разрозненными показателями; уточнение теории	– не выявляют быстрых изменений параметров; – точность зависит от объёма данных

& Предобработка (англ. pre processing) – процесс изменения исходных данных таким образом, чтобы они соответствовали условиям моделирования, существенно не искажая их значений и соотношения.

Иногда для этого процесса применяются термины пересчёт или нормализация данных [3]. Если рассматривать аналоговый по природе процесс (а в приведённом примере именно такой), то данные следует привести к значениям модельного времени. Для этого требуется осуществить ряд шагов:

1) описать в окрестностях исходных точек временного ряда гладкую кривую, наиболее адекватно отражающую исходную динамику (аппроксимировать);

2) найти уравнение получившейся кривой (полинома);

3) оценить степень погрешности (среднеквадратичное отклонение);

4) найти значения полинома в точках, соответствующих модельному времени.

При оценке адекватности аппроксимирующего закона следует руководствоваться тремя критериями:

1) коэффициент аппроксимации (среднеквадратичное отклонение) не должен превышать 0,95 (то есть он должен стремиться к единице);

2) степень полинома должна быть по возможности меньше;

3) аппроксимирующая кривая визуально должна довольно точно повторять динамику исходного ряда.

Новый ряд данных, после корректной нормализации, будет соответствовать условиям моделирования и может быть использован для просчёта в модели. Несмотря на некоторую потерю точности, это позволяет приводить данные к приемлемому для моделирования виду.

Ещё одним базовым термином, который важен при рассмотрении принципов процесса компьютерного моделирования, является термин событие.

& Событие (англ. event) – переход модели или её части в элементарное состояние, необходимое для фиксации моделируемых процессов, запуска какой-либо подпрограммы или остановки процесса просчёта модели (запланированно или в результате ошибки).

Оно позволяет проектировать процесс моделирования не только за счёт итерационного просчёта значений, но и в соответствии с некоторыми режимами её работы.

Дата добавления: 2014-12-26