
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон збереження імпульсу
|
|
|
|
Систему тіл називають замкненою (ізольованою), якщо на неї не діють зовнішні сили. Для замкненої системи геометрична сума імпульсів тіл є величиною сталою під час будь-яких рухів і взаємодії тіл системи.
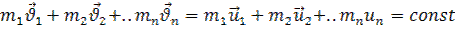
 швидкість відповідних тіл до взаємодії,
швидкість відповідних тіл до взаємодії,
 - швидкості цих тіл після взаємодії.
- швидкості цих тіл після взаємодії.
Рівняння виражає закон збереження імпульсу.
Закони збереження імпульсу можна продемонструвати на прикладі реактивного руху. Реактивний рух – це рух, який виникає, коли від тіла відокремлюється і рухається з деякою відносною швидкістю якась його частинка. Наприклад, коли із сопла ракети витікають продукти згорання палива. Під час цього ракета дістає такий самий за модулем імпульс як імпульс продуктів згорання, але напрямок буде протилежний
8 Международная система единиц SI является когерентной системой (поскольку когерентны все ее производные единицы). Основные физические величины и их единицы в системе SI представлены в таблице 1.
| Величина | Обозначение | Размерность |
| Масса | 
| килограмм |
| Длина | 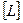
| метр |
| Время | 
| секунда |
| Заряд | 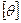
| кулон |
| Сила тока | 
| ампер |
| Сила света | 
| кандела |
| Количество вещества | 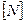
| моль |

10 Третій закон Ньютона (закон дії та протидії):
Сили, що виникають при взаємодії двох тіл, є рівними за модулем і протилежними за напрямом.
Математично це записується так 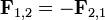 ,де
,де 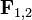 — сила, що діє на перше тіло з боку другого тіла, а
— сила, що діє на перше тіло з боку другого тіла, а 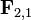 — навпаки, сила, що діє з боку першого тіла на друге тіло.
— навпаки, сила, що діє з боку першого тіла на друге тіло.
11 Близкодействие и дальнодействие —это взаимно противоположные взгляды для объяснения взаимодействия материальных структур. По концепции близко действия любое взаимодействие на материальные объекты может быть передано только между соседними точками пространства за конечный промежуток времени. Дальнодействие допускает действие на расстоянии мгновенно с бесконечной скоростью, т. е. фактически вне времени и пространства. После Ньютона эта концепция получает широкое распространение в физике, хотя он сам понимал, что введенные им силы дальнодействия (например, силы тяготения) являются лишь формальным приближенным приемом, позволяющим дать верное в некоторых пределах описание наблюдаемых явлений.
11 Чотири основних види взаємодії в природі. Фундаментальні сили, що лежать в основы механічних явищ Категорії не фундаментальних сил в механіці. Однорідна сила тяжіння, вага тіла, сили реакції. Пружна сила, деформації пружини, однорідні сили тяжіння, закон Гука. Сила тертя емпіричні закони сухого і в`язкого тертя
1 існування чотирьох фундаментальних взаємодій: гравітаційної, електромагнітної, сильної (ядерною) і слабкої взаємодій. Если гравитационное и электромагнитное взаимодействия являются дальнодействующими, распространяющимися на всю Вселенную, то слабое и сильное взаимодействия проявляются только в пределах атомного ядра и являются короткодействующими.
В механіки Ньютона лише гравітаційні і електромагнітні сили називають силами. Ядерні і слабкі взаємодії виявляються на таких малих відстанях, що для законів механіки Ньютона, не мають сенсу.
2 Фундаметальні сили, що лежать в основі механічних: сила тяготіння, вагою, си́ла тертя́, сила реакції, сила пружності
3 Нефундаментальные силы: межатомного взаимодействия, вес, инерция
4 Силою тяжіння називається сила, з якою всі тіла притягуються до Землі.
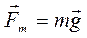
В системе отсчета, связанной с Землей, на тело массой  действует сила
действует сила  ,
,
называемая силой тяжести – сила, с которой тело притягивается Землей. Под действием этой силы все тела падают на Землю с одинаковым ускорением 
 , называемым ускорением свободного падения.
, называемым ускорением свободного падения.
Сила тяжести действует всегда, а вес проявляется лишь тогда, когда на тело кроме силы тяжести действуют еще другие силы. Сила тяжести равна весу тела только в том случае, когда ускорение тела относительно земли равно нуля. В противном случае  , где
, где  - ускорение тела с опорой относительно Земли. Если тело свободно движется в поле силы тяготения, то
- ускорение тела с опорой относительно Земли. Если тело свободно движется в поле силы тяготения, то 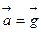 и вес тела равен нулю, т.е. тело будет невесомым.
и вес тела равен нулю, т.е. тело будет невесомым.
Вагою називається сила, з якою тіло діє на опору чи підвіс внаслідок дії земного тяжіння.
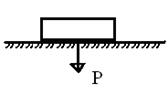

Си́ла тертя́ — це непотенційна сила, яка протидіє рухові фізичного тіла, перетворюючи його механічну енергію в тепло.
Сила реакції — сила пружності, що діє на тіло з боку опори або підвісу. Якщо тіло знаходиться на нерухомій опорі, то сила реакції чисельно дорівнює вазі тіла. Якщо опора є похилою, то сила реакції — рівнодійна сил пружності (сила нормальної реакції) і сили тертя спокою, з якою площина діє на тіло.
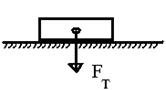
Упругую силу 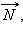 действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:
действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:  Сила
Сила 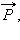 с которой тело действует на стол, называется весом тела.
с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
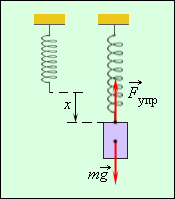 Рисунок 1.12.3.
Рисунок 1.12.3.
Деформация растяжения пружины. 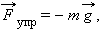

5 Тертя – один з видів взаємодії тел. Воно виникає при зіткненні двох тел. Тертя, як і всі інші види взаємодії, підкоряється третьому закону Ньютона: якщо на одне з тіл діє сила тертя, те така ж по модулі, але спрямована в протилежну сторону сила діє й на друге тіло. Сили тертя, як і пружні сили, мають електромагнітну природу. Вони виникають внаслідок взаємодії між атомами й молекулами дотичних тел.
Силами сухого тертя називають сили, що виникають при зіткненні двох твердих тіл при відсутності між ними рідкого або газоподібного прошарку. Вони завжди спрямовані по дотичній до стичних поверхонь.
Сила тертя – виникає на границі контакту тіл і спрямована протилежно напрямкові пропонованого руху тіл.
Тертя підрозділяють на тертя спокою, тертя ковзання і тертя кочення.
Сила тертя спокою дорівнює проекції зовнішніх сил на лінію контакту L тіл.
 .
.
Тертя ковзання – виникає при ковзанні одного тіла по поверхні іншого.
 ,
,
де m – коефіцієнт тертя ковзання, який залежить від природи і стану дотичних поверхонь, N – сила нормальної реакції поверхні. Сили тертя кочення звичайно досить малі.
Сила тертя кочення. Виникає з тієї причини, що точка опори при коченні тіла по поверхні зміщається вперед внаслідок деформації поверхонь, і момент сили тяжіння перешкоджає вільному коченню тіла.
 ,
,
де R – радіус тіла, що котиться, mкоч – коефіцієнт тертя кочення, який має лінійну розмірність і залежить від роду тіл.
При русі твердого тіла в рідині або газі виникає силa в'язкого тертя. Сила в'язкоготертя значно менше сили сухого тертя. Вона також спрямована убік, протилежну відносної швидкості тіла. При в'язкому терті немає тертя спокою.
Сила в'язкоготертя сильно залежить від швидкості тіла. При досить малих швидкостях F тр ~ υ, при більших швидкостях F тр ~ υ2. При цьому коефіцієнти пропорційності в цих співвідношеннях залежать від форми тіла.
12Основна задача динамики матеріальної точки і поступального руху твердого тіла. Основне рівняння динамики в проекціях на ось декартових координат та в проекціях на дотичну і нормаль до траєкторії в данній точці. Приклади розв’язання основної задачи для тіла, що ковзає з вершини гладкої сфери.
1 Практике выделяют две основные задачи динамики свободной материальной точки:
Первая задача (прямая) – считая заданным движение материальной точки массой m, определить равнодействующую сил, вызывающих это движение.
Вторая задача (обратная) – определить движение, которое будет совершать точка массы m под действием заданных сил.
При решении прямой задачи, например с помощью уравнений (4.2), нужно дважды продифференцировать заданные уравнения движения точки, подставить полученные проекции ускорения точки в уравнения (4.2) и определить равнодействующую сил, действующих на точку.
Для решения обратной задачи необходимо найти решение дифференциальных уравнений (4.2). Аналитически обратная задача решается только в частных случаях. Если аналитическое решение невозможно, задача решается численно.
2 проекціях на осі декартових координат x, y, z рівняння набуває вигляду
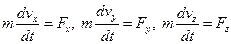 .
.
Тут 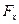 ,
, 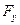 ,
,  – проекції вектора
– проекції вектора  на осі
на осі  ,
,  ,
, 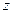 . В залежності від орієнтації вони можуть бути додатними і від’ємними. Знак проекції результуючої сили визначить і знак проекції вектора прискорення.
. В залежності від орієнтації вони можуть бути додатними і від’ємними. Знак проекції результуючої сили визначить і знак проекції вектора прискорення.
Стандартний підхід до розв’язку задач за допомогою рівняння розглянемо на прикладі аналізу ковзання невеликого бруска маси  по похилій площині, що утворює кут
по похилій площині, що утворює кут  з горизонтом. Знайдемо прискорення бруска відносно площини.
з горизонтом. Знайдемо прискорення бруска відносно площини.
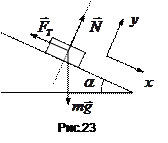 Спочатку слід вказати всі сили, що діють на брусок (рис.23). Це сила тяжіння
Спочатку слід вказати всі сили, що діють на брусок (рис.23). Це сила тяжіння 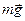 , нормальна сила реакції
, нормальна сила реакції  з боку площини і сила тертя
з боку площини і сила тертя  .
.
Далі зв’яжемо з системою відліку, похилою площиною, систему координат. Вибір осей  ,
,  ,
, 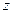 визначається характером руху тіла. В даному випадку одну із осей
визначається характером руху тіла. В даному випадку одну із осей  доцільно вибрати в напрямі руху, тобто вздовж похилої площини, як показано на рис.23. І тільки тоді приступимо до складання рівнянь руху, проектуючи на відповідні осі векторне рівняння
доцільно вибрати в напрямі руху, тобто вздовж похилої площини, як показано на рис.23. І тільки тоді приступимо до складання рівнянь руху, проектуючи на відповідні осі векторне рівняння
 .
.
Проекція на вісь  :
:  .
.
Проекція на вісь  :
: 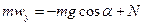 .
.
Внаслідок того, що брусок рухається тільки вздовж осі  , маємо
, маємо 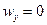 , а тому
, а тому 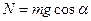 ,
,  .
.
В результаті одержимо
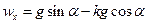 .
.
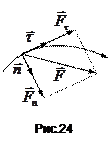 Якщо права частина цього рівняння вийде додатною, то
Якщо права частина цього рівняння вийде додатною, то  , а це означає, що вектор
, а це означає, що вектор  направлений вниз по похилій площині, і навпаки.
направлений вниз по похилій площині, і навпаки.
В проекціях на дотичну і нормаль до траєкторії в даній точці рівняння (з урахуванням отриманих в кінематиці виразів для тангенціального і нормального прискорень) буде мати вигляд
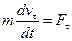 ,
, 
Тут  ,
, 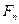 – проекції вектора
– проекції вектора  на орти
на орти 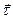 і
і  (рис.24). Вектори
(рис.24). Вектори  і
і  називають тангенціальною і нормальною складовими сили
називають тангенціальною і нормальною складовими сили  .
.
Рівняннями зручно користуватись, коли відома траєкторія руху матеріальної точки.
Приклад. Невелике тіло 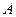 ковзає з вершини гладенької сфери радіуса
ковзає з вершини гладенької сфери радіуса 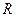 . Знайти швидкість тіла в момент відриву від поверхні сфери, якщо його початкова швидкість була рівна нулю.
. Знайти швидкість тіла в момент відриву від поверхні сфери, якщо його початкова швидкість була рівна нулю.
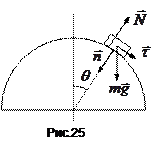 Вкажемо всі сили, силу тяжіння
Вкажемо всі сили, силу тяжіння 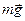 і нормальну силу реакції
і нормальну силу реакції  , які діють на тіло
, які діють на тіло 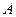 (рис.25). Далі запишемо рівняння в проекціях на орти
(рис.25). Далі запишемо рівняння в проекціях на орти 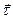 і
і  .
.
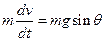 ,
,
 .
.
Перетворимо перше рівняння до вигляду, зручного для інтегрування. Скористаємось тим, що 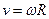 ,
,
 .
.
Перепишемо перше рівняння
 .
.
Інтегруючи його одержимо
 .
.
Із початкових умов 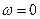 , при
, при 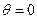 , випливає
, випливає  . Тоді останнє рівняння можна записати так
. Тоді останнє рівняння можна записати так
 .
.
З врахуванням другого рівняння  , яке відповідає умові відриву тіла
, яке відповідає умові відриву тіла 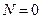 , одержуємо
, одержуємо
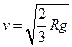 .
.
13 Величини, що зберігаються. Закони збереження, їх положення, універсальний характер, роль у фізичних дослідженнях. Імпуль системи матеріальних точок, причини зміни імпульсу у незамкнених системах, приклади такого застасувакння. Інваріантність закону збереження імпульсу відносно перетворень Галілея, його фундаментальність.
1 Всі основні одиниці фізичних величин відтворюються з найвищою точністю за допомогою міжнародних еталонів відповідних одиниць, що зберігаються у Міжнародному бюро мір та ваги у м. Севр поблизу Парижа.
2 Зако́ни збере́ження у фізиці — група законів, які стверджують, що значення певних фізичних величин не змінюється в замкненій системі з її еволюцією. Далі наводиться частковий перелік законів збереження, але на сьогодні не є доказаним фактом, що він є повний або повністю коректний (наприклад, в загальній теорії відносності, імпульс та момент імпульсу не зберігаються через те, що викривлений просторово-часовий многовид не задовольняє певним топологічним умовам):
закон збереження енергії
закон збереження маси (тільки в нерелятивістських теоріях)
закон збереження імпульсу
закон збереження моменту імпульсу
закон збереження електричного заряду
Закон збереження енергії випливає з інваріантності часу (тобто з фізичного твердження про однорідність часу), збереження імпульсу — з інваріантності зсуву (або переносу), що відповідає факту однорідності простору, збереження кутового моменту — з ізотропності простору (тобто незмінності властивостей простору в будь-якому з напрямів).
3 Силы взаимодействия между материальными точками механической системы называют внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называют внешними. Механическая система тел, на которую не действуют внешние силы, называют замкнутой (изолированной).
Рассмотрим механическую систему, состоящую из  тел, масса и скорость которых соответственно равны
тел, масса и скорость которых соответственно равны  и
и 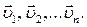
Пусть  равнодействующая всех приложенных к данному телу внутренних сил,
равнодействующая всех приложенных к данному телу внутренних сил,  равнодействующая приложенных к данному телу внешних сил. Запишем второй закон Ньютона для каждого из
равнодействующая приложенных к данному телу внешних сил. Запишем второй закон Ньютона для каждого из 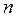 тел механической системы:
тел механической системы:
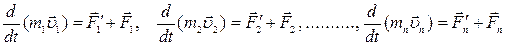 .
.
Сложим почленно эти уравнения:
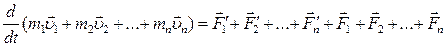 .
.
Согласно третьему закону Ньютона силы, действующие между телами системы,
равны и противоположно направлены, поэтому геометрическая сумма внутренних сил равна нулю и 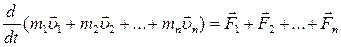 .
.
Векторная сумма импульсов тел, входящих в систему, 
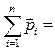
 , называется импульсом системы. Таким образом,
, называется импульсом системы. Таким образом,
 (2.5.1)
(2.5.1)
Следовательно, закон изменения импульса гласит: скорость изменения импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В замкнутой системе  , поэтому
, поэтому 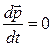 и, следовательно,
и, следовательно, 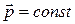 .
.
Последнее выражение является законом сохранения импульса: импульс замкнутой системы есть величина постоянная, т.е. не изменяется с течением времени.
Хотя закон сохранения импульса получен как следствие законов Ньютона, он справедлив не только в классической физике, но и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). В силу своей универсальности закон сохранения импульса является фундаментальным законом природы. Отметим, что импульс сохраняется и для незамкнутой системы, если геометрическая сумма внешних сил равна нулю.Причина изменение импульса, т.к. на тела в этой системе действуют внешние силы.
7 Закони збереження імпульсу можна продемонструвати на прикладі реактивного руху. Реактивний рух – це рух, який виникає, коли від тіла відокремлюється і рухається з деякою відносною швидкістю якась його частинка. Наприклад, коли із сопла ракети витікають продукти згорання палива. Під час цього ракета дістає такий самий за модулем імпульс як імпульс продуктів згорання, але напрямок буде протилежний
8 инвариантных преобразований (например, в механике – преобразования Галилея, в электродинамике – преобразования Лоренца). В результате инвариантных преобразований Галилея сохраняются законы механики Ньютона, а в результате преобразований Лоренца в электродинамике сохраняется вид уравнений Максвелла в различных инерциальных системах координат
Во всех перечисленных случаях – различного рода физических процессах и математических преобразованиях – некоторые ветчины или параметры остаются неизменными. Оказывается, что тем законам в физике или преобразованиям в математике соответствует некоторая симметрия.
14 Центр мас системи матеріальних точок, швидкість центра мас, імпульс системи. Рівняння руху ценра мас, приклади на рух ценру мас системи. Системи відляку системи мас (Цсв), відмінні особливості ц-системи, приклад системи з 2х матеріальних точок.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1795; Нарушение авторских прав?; Мы поможем в написании вашей работы!