
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямими перетвореннями Галілея
|
|
|
|
Плоский рух абсолютно твердого тіла (АТТ). Приклади розбиття плоского руху АТТ на поступальний і обертальний, миттєва вісь обертання, абсолютний характер кутової швидкості. Швидкість довільної точки тіла при плоскому русі. рДодавання кутових швидкостей, пиклад круглого конуса з закріпленою шарнірно вершиною, який котиться по горизонтальній площини.

Мгновенная ось вращения перемещается вместе с телом. Каждому моменту времени (мгновению) соответствует свое положение мгновенного центра скоростей и свое положение мгновенной оси. Например, в рассмотренном опыте мгновенная ось перемещается вместе с тележкой.
Кутова швидкість – векторна фізична величина, що характеризує бистроту і напрям обертання.
Кутова швидкість – вектор, напрямлений вздовж осі обертання таким чином, щоб з його кінця було видно обертання, що здійснюється проти годинникової стрілки (правило правого гвинта).
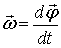 Кутова швидкість матеріальної тачки чи тіла це фізична величина, яка визначається відношенням вектора елементарного повороту до тривалості цього повороту:.
Кутова швидкість матеріальної тачки чи тіла це фізична величина, яка визначається відношенням вектора елементарного повороту до тривалості цього повороту:.
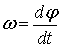 Напрям вектора, як і, визначається за правилом правого гвинта вздовж осі О (рис.2). В скалярному вигляді:
Напрям вектора, як і, визначається за правилом правого гвинта вздовж осі О (рис.2). В скалярному вигляді:
Якщо 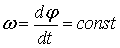
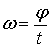 то такий рух називається рівномірним обертальним рухом. При рівномірному обертальному русі кутову швидкість визначають за формулою:
то такий рух називається рівномірним обертальним рухом. При рівномірному обертальному русі кутову швидкість визначають за формулою:
Відповідно до попереднього, розмірність кутової швидкості: 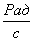
зглянемо тверде тіло, що обертається навколо нерухомої осі (рис. 106), на якому також зображено:
– траєкторію довільної точки  тіла;
тіла;
– вектор її швидкості 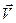 , дотичний до траєкторії і напрямлений в бік обертання;
, дотичний до траєкторії і напрямлений в бік обертання;
– вектор кутової швидкості тіла 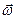 з довільної її точки
з довільної її точки 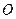 в бік, звідки обертання тіла видно проти руху годинникової стрілки;
в бік, звідки обертання тіла видно проти руху годинникової стрілки;
 – радіус-вектор точки
– радіус-вектор точки  . Початок його знаходиться в центрі
. Початок його знаходиться в центрі 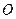 .
.
 Зауважимо, що вектор
Зауважимо, що вектор 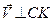 (бо вектор швидкості перпендикулярний до радіуса обертання) і
(бо вектор швидкості перпендикулярний до радіуса обертання) і 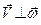 (тому що вектор швидкості знаходиться в площині траєкторії, яка в даному випадку перпендикулярна до осі обертання). Отже, вектор
(тому що вектор швидкості знаходиться в площині траєкторії, яка в даному випадку перпендикулярна до осі обертання). Отже, вектор 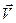 є перпендикулярним до площини
є перпендикулярним до площини 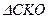 , тобто до площини, яка проходить через вектори
, тобто до площини, яка проходить через вектори 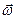 і
і  . Величина вектор швидкості визначається за формулою (2.44)
. Величина вектор швидкості визначається за формулою (2.44)
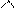
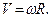 (а)
(а)
З 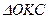 маємо
маємо 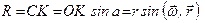 .
.
Підставивши значення 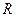 у формулу (а), отримаємо
у формулу (а), отримаємо
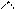
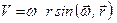 .
.
Отже, модуль швидкості дорівнює модулю векторного добутку 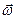 і
і  , який можна записати двояко:
, який можна записати двояко:  або
або 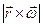 . З визначення векторного добутку випливає, що тільки добуток
. З визначення векторного добутку випливає, що тільки добуток 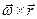 буде визначати вектор, який співпадає за напрямом з вектором швидкості
буде визначати вектор, який співпадає за напрямом з вектором швидкості 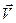 , тобто
, тобто
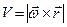 ,
,
або
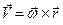 . (2.53)
. (2.53)
6;7 Опис переходу від однієї інерціальної системи відліку (К св.) до іншої (К1 св.). Перетворення швидкості та прискорення матеріальної точки при переході до К1 -системи, яка обертається з постійною кутовою швидкістю 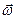 навколо осі, в нерухомій К-системи.
навколо осі, в нерухомій К-системи.
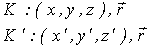 Час в обох системах протікає однаково. Тому положення точки в момент часу характеризується як координатами так і радіус-вектором в обох системах:
Час в обох системах протікає однаково. Тому положення точки в момент часу характеризується як координатами так і радіус-вектором в обох системах:
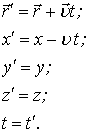 Значення цих величин в рухомій системі координат називається
Значення цих величин в рухомій системі координат називається
 Рівняння руху точки в нерухомій системі відліку описується оберненими перетвореннями Галілея:
Рівняння руху точки в нерухомій системі відліку описується оберненими перетвореннями Галілея:
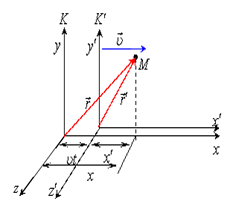
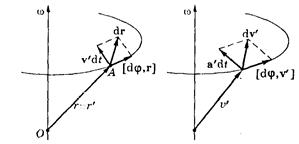
 Нехай СВ k і
Нехай СВ k і 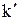 рухаються довільно відносно одна одній. Положення тіла в СВ
рухаються довільно відносно одна одній. Положення тіла в СВ  характеризується величинами:
характеризується величинами: 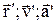 . У СВ k:
. У СВ k: 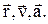 Положення СВ k' відносно k характеризується величинами
Положення СВ k' відносно k характеризується величинами 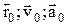 . Нехай СВ
. Нехай СВ 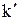 рухається поступально відносно СВ k. З малюнка випливає:
рухається поступально відносно СВ k. З малюнка випливає:
 .
.
При нескінченно малому переміщенні:
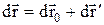 .
.
Розділимо обидві частини останньої рівності на dt:
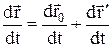 .
.
Одержуємо закон перетворення швидкостей: 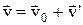 .
.
Продифференціювавши останнє рівняння за часом, одержимо закон перетворення прискорень:
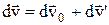 ,
, 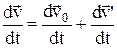 ,
, 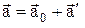 .
.
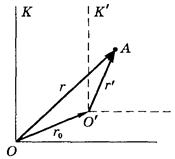
Нехай СВ 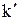 обертається з постійною
обертається з постійною 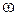 навколо осі, яка нерухома в СВ k. Нехай початок відліку СВ k і
навколо осі, яка нерухома в СВ k. Нехай початок відліку СВ k і 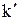 збігаються. Тоді радіус–вектор точки А в обох СВ однаковий. З малюнка випливає:
збігаються. Тоді радіус–вектор точки А в обох СВ однаковий. З малюнка випливає:
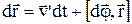 .
.
Розділимо обидві частини останньої рівності на dt.
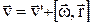 ,
, 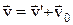 .
.
Нехай за проміжок часу dt усі вектори одержали малі збільшення, тобто
 .
.
Визначимо 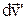 . З малюнку випливає:
. З малюнку випливає:
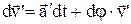 .
.
Підставимо 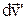 та
та 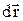 у рівняння
у рівняння 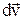 :
:
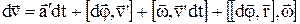 .
.
Розділимо останнє рівняння на dt:
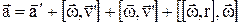
 ,
,
де 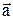 і
і 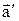 – прискорення точки в СВ k і
– прискорення точки в СВ k і 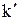 .
.
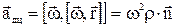 – доцентрове прискорення, яке спрямовано уздовж осі до центру обертання.
– доцентрове прискорення, яке спрямовано уздовж осі до центру обертання.
 – коріолісово прискорення, що виникає внаслідок руху тіла в СВ, що обертається.
– коріолісово прискорення, що виникає внаслідок руху тіла в СВ, що обертається.
Таким чином, повне прискорення точки можна представити у вигляді:
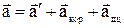 .
.
Якщо система відліку k' рухається поступально щодо системи відліку k із прискоренням 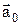 , то остання формула приймає наступний вигляд:
, то остання формула приймає наступний вигляд:
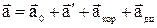 .
.
8 Опис переходу від однієї інерціальної системи відліку (К св.) до іншої (К1 св.). Перетворення швидкості та прискорення матеріальної точки при переході до К1 -системи, яка обертається з постійною кутовою швидкістю навколо осі, в що рухається поступально зі швидкістю V0 та прискорення а0 по відношенню до К1 -системи
9 Інерціальні системи відліку (ІСВ) та неінерціальні системи відліку. Закони інерції (1 з-н Ньютона). Властивості простору і часу по відношенню до ІСВ. Принцип відносності Галілея. Перетворення Галілея. Поняття вільного тіла і замкненої системи тіл. Межи застасувакння класичної механіки (за швидкостями і розмірами)
I закон Ньютона формулюється так: всяке тіло зберігає стан спокою або рівномірного прямолінійного руху доти, поки дія з боку інших тіл не змусить його змінити цей стан. I закон Ньютона називається ще законом інерції
Властивість тіл зберігати стан спокою або рівномірного прямолінійного руху без дії на них інших тіл називають інертністю.
хай у початковий момент часу 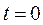 дві інерціальні системи від-ліку
дві інерціальні системи від-ліку  і
і 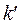 співпадають (рис. 4.3), а з плином часу система
співпадають (рис. 4.3), а з плином часу система 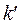 рухається відносно умовно нерухомої системи
рухається відносно умовно нерухомої системи  з постійною швидкістю
з постійною швидкістю 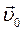 так, що осі
так, що осі 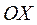 і
і  збігаються, осі
збігаються, осі  і
і 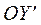 , а також
, а також 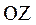 і
і 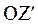 попарно паралельні між собою. Знайдемо зв'язок між координатами матеріальної точки в системах
попарно паралельні між собою. Знайдемо зв'язок між координатами матеріальної точки в системах  і
і 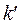 у будь-який момент часу
у будь-який момент часу 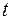 (рис. 4.3). Якщо вважати, що час в обох системах відліку плине однаково, тобто що
(рис. 4.3). Якщо вважати, що час в обох системах відліку плине однаково, тобто що 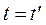 , то:
, то:
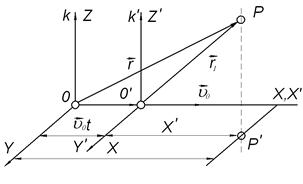

Рис. 4.3
Систему рівнянь (4.19) називають перетвореннями Галілея. Вони дають змогу одержати закон руху відносно однієї з інерціальних систем, якщо він відомий відносно іншої, шляхом заміни відповідних координат.
Якщо при 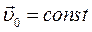 система
система 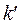 рухається в довільному напрямку відносно
рухається в довільному напрямку відносно  , то перетворення Галілея приймають вигляд:
, то перетворення Галілея приймають вигляд:
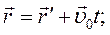

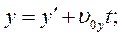
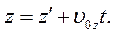 (4.20)
(4.20)
Перетворення Галілея застосовні в області механіки малих швидкостей і не застосовуються в механіці великих швидкостей, оскільки при великих швидкостях процесів час у різних інерціальних системах відліку плине неоднаково, тобто 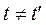 : Продиференціювавши за часом рівняння (4.19) і (4.20), знайдемо зв’язок між швидкостями точки Р відносно систем
: Продиференціювавши за часом рівняння (4.19) і (4.20), знайдемо зв’язок між швидкостями точки Р відносно систем  і
і  відповідно:
відповідно:
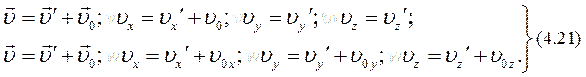
Якщо  і
і 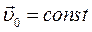 , то і
, то і 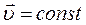 , тобто якщо точка Р відносно системи
, тобто якщо точка Р відносно системи 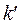 рухається рівномірно і прямолінійно, а сама система
рухається рівномірно і прямолінійно, а сама система 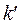 відносно
відносно  рухається теж рівномірно і прямолінійно, то і точка Р від-носно системи
рухається теж рівномірно і прямолінійно, то і точка Р від-носно системи  рухається рівномірно і прямолінійно. Ми дійшли виснов-ку, що перший закон Ньютона виконується у всіх інерціальних системах відліку.
рухається рівномірно і прямолінійно. Ми дійшли виснов-ку, що перший закон Ньютона виконується у всіх інерціальних системах відліку.
Якщо  , а
, а 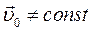 , тоді і
, тоді і 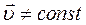 тобто відносно неінерціальних систем відліку перший закон Ньютона не виконується.
тобто відносно неінерціальних систем відліку перший закон Ньютона не виконується.
Продиференціювавши рівняння 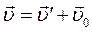 за часом, знайдемо зв'я-зок між прискореннями точки Р відносно розглянутих систем відліку:
за часом, знайдемо зв'я-зок між прискореннями точки Р відносно розглянутих систем відліку:
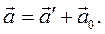 (4.22)
(4.22)
Якщо  , тобто якщо система
, тобто якщо система 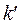 відносно системи
відносно системи  рухається нерівномірно (системи взаємно неінерціальні), то сила, яка діє на точку Р, різна в різних системах відліку:
рухається нерівномірно (системи взаємно неінерціальні), то сила, яка діє на точку Р, різна в різних системах відліку:
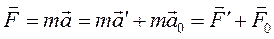 ,
,
і другий закон Ньютона (як і перший) не виконується відносно системи 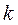 . Я Якщо
. Я Якщо 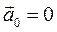 , то
, то 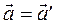 і
і  , тобто другий закон Ньютона вико-нується відносно різних інерціальних систем відліку.
, тобто другий закон Ньютона вико-нується відносно різних інерціальних систем відліку.
З співвідношень 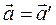 і
і  знаходимо:
знаходимо:
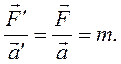 (4.23)
(4.23)
Таким чином, рівняння Ньютона для матеріальної точки, а отже, і для довільних систем матеріальних точок, однакові у всіх інерціальних систе-мах відліку. Це твердження називають механічним принципом відносності або принципом відносності Галілея, який встановив цей принцип, і часто формулюють цей принцип у такий спосіб: "Всі механічні явища у всіх інер-ціальних системах відліку протікають однаковим чином”.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 703; Нарушение авторских прав?; Мы поможем в написании вашей работы!