Примеры решения задач по теме №1

Пример 1.1. Самолет движется со скоростью 18 км/ч. С некоторого момента он начинает двигаться с ускорением a в течение 10 с, а последние 110 м проходит за одну секунду. Определить ускорение и конечную скорость самолета.

Дано: 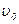=18 км/ч=5м/с,

t₁=10 с,

t₂=1 с,

S₂=110 м.

Найти: a,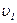

Решение

Весь путь, проделанный самолетом, делится на два S₁ и S₂ (рис.1).

Рис. 1.

Запишем для двух этих участков уравнения движения:

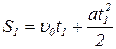; (1.1.1)

(1.1.2)

и законы изменения скорости:

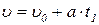; (1.1.3)

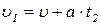. (1.1.4)

Подставим (1.1.3) в (1.1.2):

. (1.1.5)

Выразим a:

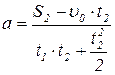. (1.1.6)

Подставим в (1.1.6) числовые данные:

.

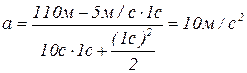Теперь подставим (1.1.3) в (1.1.4) и вычислим конечную скорость:

.

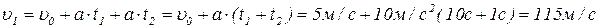Ответ: ускорение самолета a=10м/с², конечная скорость самолета 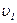=115м/с.

Пример 1.2. Колесо вращается с частотой 180об/мин. С некоторого момента колесо начинает вращаться равнозамедленно с угловым ускорением 3 рад/с². Через какое время колесо остановится? Найти число оборотов колеса до остановки.

Дано: ν = 180об/мин=3об/с,

ε = 3 рад/с².

Найти: t, n.

Решение

Запишем уравнение движения тела, совершающего равноускоренное, вращательное движение:

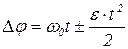(1.2.1)

и закон изменения скорости

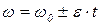. (1.2.2)

Здесь Δφ – угол поворота тела за время t, ω₀ и ω – угловая скорость тела в начальный момент времени и в момент времени t соответственно, ε – угловое ускорение.

Угол поворота Δφ связан с числом оборотов n соотношением:

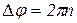. (1.2.3)

Начальную угловую скорость ω₀ найдем из соотношения:

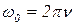. (1.2.4)

С учетом (1.2.3) и (1.2.4), а также с учетом того, что колесо движется равнозамедленно, перепишем (1.2.1):

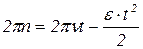. (1.2.5)

Из уравнения (1.2.2) найдем время до остановки колеса, т.е. время, когда угловая скорость ω стала равна нулю:

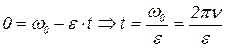. (1.2.6)

Рассчитаем время t:

.

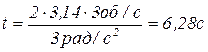Теперь подставим (1.2.6) в (1.2.5):

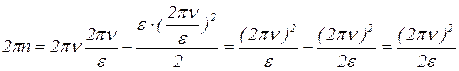. (1.2.7)

Выразим из (1.2.7) число оборотов n и подставим числовые данные:

.

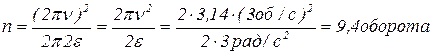Ответ: колесо остановится через 6,28 с; число оборотов n=9,4 оборота.

Пример 1.3. Шар массой 2 кг, движущийся горизонтально со скоростью 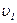=4 м/с, столкнулся с неподвижным шаром массой 3 кг. Считая удар центральным и абсолютно неупругим, найти количество теплоты, выделившееся при ударе.

Дано: m₁ = 2 кг,

m₂ = 3 кг,

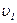= 4 м/с,

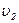= 0 м/с.

Найти: Q.

Решение

Запишем закон сохранения импульса:

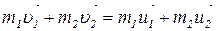. (1.3.1)

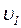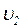Здесь и – скорости первого и второго шаров до удара соответственно, u₁ и u₂ – скорости первого и второго шаров после удара соответственно. После неупругого столкновения тела движутся с одинаковой скоростью, поэтому u₁ = u₂ = u. Запишем проекцию уравнения (1.3.1) на направление движения шаров с учетом того, что 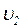=0 м/с:

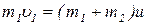. (1.3.2)

При неупругом ударе закон сохранения энергии не выполняется. Разность между энергией системы до удара (Е_К1) и энергией после удара (Е_К2) равна количеству теплоты, выделившемуся при ударе:

. (1.3.3)

Кинетическая энергия системы до удара:

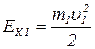. (1.3.4)

Кинетическая энергия системы после удара:

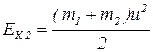. (1.3.5)

Выразим из (1.3.2) u и подставим в (1.3.5):

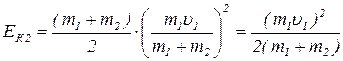. (1.3.6)

С учетом (1.3.4) и (1.3.6) вычислим количество теплоты Q:

.

Ответ: количество теплоты, выделившееся при ударе Q=9,6 Дж.

Пример 1.4. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 12 кг. Найти момент инерции барабана, если груз опускается с ускорением 1,81 м/с². Барабан считать однородным цилиндром. Трением пренебречь.

Дано: R=0,5м,

m=12 кг,

a=1,81 м/с².

Найти: J.

Решение

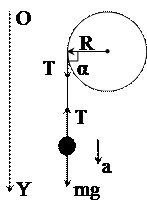
Рис. 2

Запишем основной закон динамики вращательного движения:

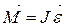. (1.4.1)

Здесь J – момент инерции цилиндра относительно оси вращения, проходящей через центр масс, ε – угловое ускорение (ускорение вращательного движения), M – момент силы, заставляющей барабан вращаться. Такой силой является сила натяжения шнура Т.

Модуль момента силы равен:

. (1.4.2)

Из рис. 2 видно, что α=90⁰, поэтому:

. (1.4.3)

Угловое ускорение ε связано с линейным ускорением a соотношением:

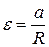, (1.4.4)

где R – радиус барабана.

С учетом (1.4.3) и (1.4.4) перепишем (1.4.1) в скалярном виде (вектор М и вектор ε направлены в одну сторону):

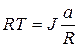. (1.4.5)

Выразим из (1.4.5) J:

. (1.4.6)

Силу натяжения шнура Т найдем из второго закона Ньютона, записанного для поступательно движущегося груза (рис. 2):

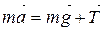. (1.4.7)

Сила натяжения шнура, вращающая барабан и сила, действующая на груз, равны по модулю и направлены в противоположные стороны. Проекция уравнения (1.4.7) на ось OY имеет вид:

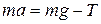. (1.4.8)

Выразим из (1.4.8) Т и подставим полученное выражение в (1.4.6):

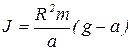. (1.4.9)

Проверим размерность:

.

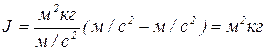Подставим в (1.4.9) числовые данные:

.

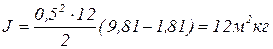Ответ: момент инерции барабана J=12 м²кг.

Пример 1.5. Шар массой 0,25 кг и радиусом 3 см катится без скольжения по горизонтальной плоскости с частотой вращения 4 об/с. Найти кинетическую энергию шара.

Дано: m=0,25 кг,

R=3 см=3∙10^-2 м,

ν= 4 об/с.

Найти: E_К.

Решение

Кинетическая энергия шара, который катится по горизонтальной плоскости без скольжения, складывается из энергии поступательного и вращательного движения:

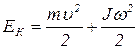, (1.5.1)

где m – масса шара, 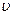– линейная скорость (скорость поступательного движения), J – момент инерции шара относительно оси вращения, проходящей через центр масс, ω – угловая скорость (скорость вращательного движения).

Известно, что для шара радиусом R

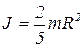. (1.5.2)

Угловая скорость ω связана с линейной скоростью 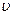соотношением:

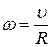, (1.5.3)

а с линейной частотой ν соотношением

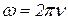. (1.5.4)

Подставим (1.5.2), (1.5.3) и (1.5.4) в (1.5.1) и сделаем необходимые преобразования:

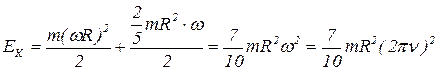. (1.5.5)

Подставим в (1.5.5) числовые данные:

.

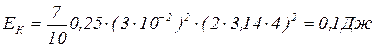Ответ: кинетическая энергия шара Е_К=0,1 Дж.

Дата добавления: 2014-12-26