Тема 9. Эффективное кодирование

Задача 9.1.

Используя методику Шеннона-Фано, провести эффективное кодирование ансамбля из восьми знаков , вероятности которых приведены в таблице 2.

Таблица 2

Знаки	Вероятности
	1/2
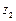
	1/4
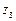
	1/8
	1/16
	1/32
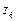
	1/64
	1/128
	1/128

Задача 9.2.

Для построенного в условиях задачи 9.1 эффективного кода определить среднее число символов на знак и энтропию, сравнить и объяснить результаты.

Задача 9.3.

Определить среднюю длину кодовой комбинации при эффективном кодировании знаков следующего ансамбля:

.

Задача 9.4.

Построить эффективный код для ансамбля, состоящего из двух знаков:

.

Вычислить энтропию и среднее число символов на знак.

Задача 9.5.

В условиях задачи 9.4 провести эффективное кодирование блоками, содержащими по два знака. Вычислить среднее число символов на знак и сравнить с результатами задачи 9.4

Задача 9.6.

Используя методику Хаффмена, осуществить эффективное кодирование ансамбля, заданного в задаче 9.3. Построить кодовое дерево. Проверить свойство префиксности полученного кода.

Задача 9.7.

Заданы вероятности четырех сообщений:

; ; ; .

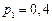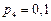Построить эффективные коды с использованием методик Шеннона-Фано и Хаффмена.

Задача 9.8.

Определить среднюю длину кодовой комбинации при эффективном кодировании по методике Хаффмена знаков ансамбля, приведенного в таблице 3.

Таблица 3

Знаки	Вероятность
	0,22
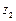
	0,20
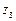
	0,16
	0,16
	0,10
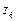
	0,10
	0,04
	0,02

Задача 9.9.

В таблице 4 приведены вероятности появления сообщений ансамбля 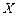и различные варианты кодов для этого ансамбля.

а) Какие из приведенных кодов однозначно декодируемы (каждое кодовое слово может быть идентифицировано в последовательности)?

б) Какие из приведенных кодов мгновенно декодируемы (конец каждого кодового слова может быть идентифицирован без учета последующих символов)?

в) Вычислить среднюю длину кодового слова для кодов, найденных в пункте а).

Таблица 4

Символ		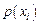A	B	C	D	E

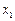
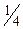
Дата добавления: 2014-12-26