Тема 11. Построение групповых кодов

Задача 11.1.

Определить кодовое расстояние между двумя двоичными кодовыми комбинациями:

1111110 и 0100100.

Задача 11.2.

Определить избыточность двоичного кода, предназначенного для передачи 16 команд, если длина кода .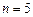

Задача 11.3.

Определить число разрядов кодовой комбинации для передачи 8 сообщений неизбыточным двоичным кодом.

Задача 11.4.

Построить групповой код для передачи 15 слов, исправляющий одиночные ошибки (нулевая комбинация не используется).

Задача 11.5.

Построить групповой код для передачи 31 слова, исправляющего одиночные ошибки (нулевая комбинация не используется).

Задача 11.6.

Построить опознаватели для исправления всех одиночных и двойных ошибок для кода, предназначенного для передачи 3 слов.

Задача 11.7.

Построить код длиной 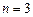, предназначенный для обнаружения всех однократных ошибок: .

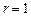Задача 11.8.

Определить число разрешенных комбинаций плотноупакованного кода длиной 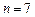, предназначенного для исправления однократных ошибок: .

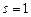Задача 11.9.

Построить групповой код, предназначенный для передачи 15 слов (нулевая комбинация не используется), способный исправлять одиночные и обнаруживать двойные ошибки: , .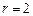

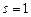Задача 11.10.

Код (32,6), использованный на космическом корабле Mariner 9, названный кодом Рида-Мюллера, имел минимальное кодовое расстояние между словами равное 16. Определить, какое максимальное число ошибок в разрядах он позволял обнаруживать.

Задача 11.11.

Пусть код длиной 7 допускает возникновение ошибок только в одном из следующих векторов:

0000000,

0000001,

0000011,

0000111,

0001111,

0011111,

0111111,

1111111.

Построить бинарный код длиной 7, корректирующий ошибки подобного рода с максимально возможной кратностью.

Задача 11.12.

Используя таблицу 5, составить правила построения кода (8,2), исправляющего все одиночные и двойные ошибки.

Таблица 5

Номер разряда	Опознаватель

Задача 11.13.

Для кода (8,2), построенного по условию предыдущей задачи, построить систему разделенных проверок (проверочных равенств) для декодирования информационных символов.

Задача 11.14.

Задан код (7,3), исправляющий одиночные ошибки. Вычислить вероятность ошибочного декодирования.

Задача 11.15.

Показать, что при длинах кодов 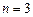и 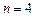невозможно построить код, исправляющий одиночные ошибки для ансамбля, состоящего более чем из двух сообщений.

Дата добавления: 2014-12-26