
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 15. Обнаружение и различение сигналов
|
|
|
|
Задача 15.1.
По каналу связи, в котором действует аддитивная стационарная помеха, передается периодическая последовательность прямоугольных импульсов. Параметры полезного сигнала: величина  , период следования
, период следования 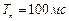 . Помеха имеет нормальный закон распределения. Среднеквадратическое значение помехи
. Помеха имеет нормальный закон распределения. Среднеквадратическое значение помехи  , математическое ожидание
, математическое ожидание  . Обработка сигналов на принимающей стороне осуществляется методом синхронного накопления. Определить время обработки сигналов, необходимое для обеспечения превышения сигнала над помехой в 4 раза.
. Обработка сигналов на принимающей стороне осуществляется методом синхронного накопления. Определить время обработки сигналов, необходимое для обеспечения превышения сигнала над помехой в 4 раза.
Решение.
Упрощенная схема приемника с синхронным накоплением представлена на рисунке 13.

Рис. 13.
Усилитель приемника в исходном состоянии заперт. Строб-сигнал поступает синхронно с полезным сигналом и обеспечивает отпирание приемника на время подачи полезного сигнала.
Отношение сигнал/помеха на выходе накопителя в случае стационарной помехи
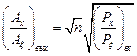 ,
,
где  ─ отношение мощностей сигнала и помехи на входе приемника;
─ отношение мощностей сигнала и помехи на входе приемника; 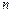 ─ количество отсчетов за время приема.
─ количество отсчетов за время приема.
В нашем случае
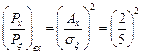 .
.
Продолжительность обработки сигналов в приемнике
 .
.
По условию задачи
 .
.
Тогда необходимое время наблюдения

Задача 15.2.
Необходимо осуществить обнаружение постоянного сигнала величиной  на фоне аддитивной помехи с нормальным распределением и средним значением, равным нулю. Метод приема – однократный отсчет. Произвести синтез приемного устройства, работающего на основе критерия максимума правдоподобия и определить пороговый уровень.
на фоне аддитивной помехи с нормальным распределением и средним значением, равным нулю. Метод приема – однократный отсчет. Произвести синтез приемного устройства, работающего на основе критерия максимума правдоподобия и определить пороговый уровень.
Решение.
Так как по условию задачи помеха аддитивна и выборка  представляет одномерную величину, то функции правдоподобия
представляет одномерную величину, то функции правдоподобия 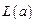 и
и  определяются законом распределения помехи:
определяются законом распределения помехи:
 ;
;
 .
.
Отношение правдоподобия при этом
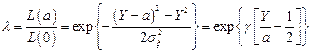 ,
,
где  .
.
При использовании критерия максимума правдоподобия пороговое значение отношения правдоподобия  . Тогда, приравняв полученное выражение для отношения правдоподобия единице, получим условие для порогового значения входного сигнала
. Тогда, приравняв полученное выражение для отношения правдоподобия единице, получим условие для порогового значения входного сигнала  :
:
 ,
,
откуда получаем
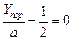 ,
,
или
 .
.
Таким образом, приемное устройство представляет собой устройство сравнения, сравнивающее входной сигнал с пороговым уровнем 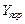 , равным половине величины полезного сигнала.
, равным половине величины полезного сигнала.
Если входной сигнал превышает пороговый уровень в 1В, то выносится решение, что во входном сигнале имеется полезный сигнал. Если же входной сигнал равен или меньше 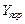 , то выносится решение об отсутствии полезного сигнала.
, то выносится решение об отсутствии полезного сигнала.
Задача 15.3.
Решить задачу 15.2 для случая, когда используется критерий идеального наблюдателя и дополнительно известно, что отношение априорных вероятностей отсутствия и присутствия полезного сигнала в принятом  и среднеквадратическое значение помех
и среднеквадратическое значение помех 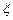 равно
равно 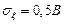 .
.
Решение.
При использовании критерия идеального наблюдателя пороговое значение отношения правдоподобия  .
.
Тогда, приравнивая правую часть полученного выражения для отношения правдоподобия и пороговое значение  , получим следующее выражение для порогового уровня:
, получим следующее выражение для порогового уровня:
 .
.
Задача 15.4.
Решить задачу 15.5 для случая, когда используется критерий Неймана-Пирсона и дополнительно известно, что среднеквадратическое значение помех  и вероятность ошибки первого рода при принятии решения не должна превышать величины
и вероятность ошибки первого рода при принятии решения не должна превышать величины  .
.
Решение.
Если перейти от переменных 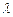 к переменным
к переменным  , то искомое пороговое значение
, то искомое пороговое значение 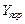 можно определить из следующего соотношения:
можно определить из следующего соотношения:
 .
.
После замены  получаем уравнение для нахождения
получаем уравнение для нахождения 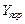 :
:
 ,
,
где 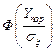 ─ функция Лапласа.
─ функция Лапласа.
По условию задачи
 .
.
По таблицам функций Лапласа находим
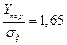 ,
,
откуда искомый пороговый уровень
 .
.
Задача 15.5.
На вход приемного устройства поступает смесь полезного гармонического сигнала 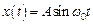 с амплитудой
с амплитудой  и аддитивной помехи, распределенной по нормальному закону с нулевым средним и среднеквадратическим значением
и аддитивной помехи, распределенной по нормальному закону с нулевым средним и среднеквадратическим значением  . Произведено два замера входного сигнала
. Произведено два замера входного сигнала  в моменты времени
в моменты времени  и
и 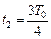 , где
, где 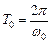 − период сигнала
− период сигнала 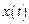 . Априорные вероятности значений
. Априорные вероятности значений  и
и 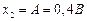 соответственно
соответственно  . Найти апостериорные вероятности значений
. Найти апостериорные вероятности значений  и
и  после указанных выше замеров.
после указанных выше замеров.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 820; Нарушение авторских прав?; Мы поможем в написании вашей работы!