Тема 16. Оценка параметров сигналов

Задача 16.1.

Пусть 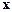─ 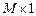-векторы, 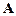─ 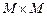-матрица. Убедитесь в справедливости формул матричного анализа:

,

.

Задача 16.2.

Пусть линейная модель идентифицируемой модели имеет вид:

,

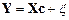где

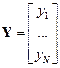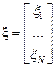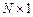, , -векторы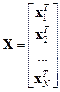 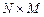-матрица

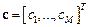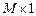─ -искомый вектор.

Показать, что

,

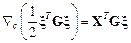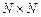где ─ вещественная -матрица.

Задача 16.3.

Заданы:

матрица 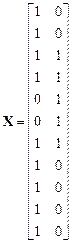, вектор .

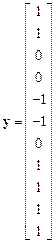Вычислить МНК-оценку 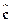вектора 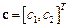для случаев:

, , .

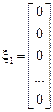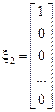Сравнить оценки, объяснить результат.

Задача 16.4.

Определить параметры 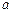, 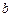нелинейной модели

.

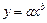Указание.

Перейти от исходной модели к линейной по параметрам.

Задача 16.5.

Производится оценка амплитуды сигнала 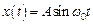. Время наблюдения . Помехи типа белого шума со спектральной плотностью .

Найти, каково должно быть среднее значение параметра 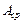, чтобы для относительной погрешности оценки выполнялось равенство:

.

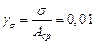Задача 16.6.

На вход оптимального фильтра Норса поступает сигнал прямоугольной формы длительности с амплитудой 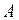. Определить передаточную функцию фильтра при условии, что в канале действует белый гауссов шум.

Заключение

Дадим некоторые общие рекомендации по работе с учебным пособием «Практикум по теории информации». Настоящий практикум тесно связан с ранее изданным учебным пособием «Лекции по теории информации». В частности, названия тем в точности соответствуют названиям лекций. Таким образом, после каждой лекции следует проработать соответствующую тему настоящего практикума.

Не следует начинать решение задач по очередной теме до тех пор, пока не усвоены основные положения соответствующей лекции. Работа облегчается тем, что, в основном, сохранены те же, что и в лекциях, обозначения. Число контрольных задач для самостоятельного решения в каждой теме сравнительно невелико. Большое число задач по курсу «Теория информации» можно найти в комплекте аттестационных педагогических материалов.

В заключение подчеркнем, что приведенные примеры решения не следует слепо копировать. Обычно существует несколько способов решения или, по крайней мере, оформления решения задачи. Нахождение таких оригинальных способов решения и интерпретации найденных решений принесет большую пользу и удовольствие.

Конечно, приведенные здесь задачи носят, в основном, учебный характер. Поэтому используемые модели и исходные данные чрезвычайно просты. Тем не менее рекомендуем результаты решений соотносить с ситуациями, которые могут возникать на практике. При внимательном рассмотрении можно заметить, что многие задачи дают богатую пищу для анализа и интерпретации реальных моделей.

Приложение

Таблица неприводимых многочленов

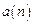
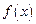
			Exp
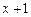
			1 P
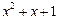
			3 P
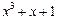
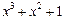
			7 P 7 P
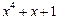
			15 P 15 P
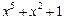
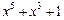
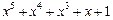
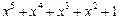
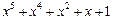
			31 P 31 P 31 P 31 P 31 P 31 P
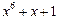
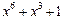
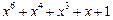
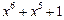
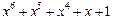
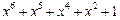
			63 P 63 P 63 P 63 P 63 P 63 P
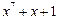
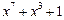
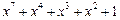
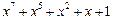
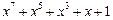
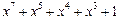
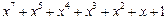
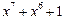
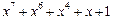
			127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P 127 P
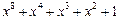
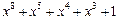
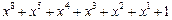
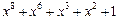
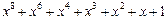
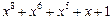
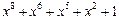
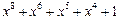
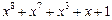
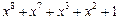
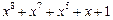
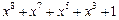
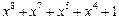
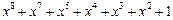
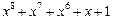
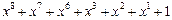
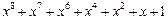
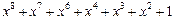
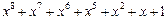
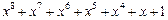
			255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P 255 P
		…	…
		…	…
		…	…
		…	…
		…	…
		…	…
		…	…
…	…	…	…

Пояснения к таблице:

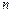─ степень многочлена;

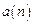─ число примитивных многочленов;

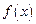─ неприводимый многочлен;

Exp ─ минимальное значение 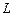такое,
что 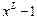является делителем .
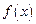«P» означает, что многочлен является примитивным.

Примечание:

В таблице приведены коэффициенты для многочленов до 7-ой степени, а также число примитивных многочленов до 15-ой степени.

Для самостоятельного получения значений более высоких степеней рекомендуем воспользоваться материалами, приведенными в [9].

Дата добавления: 2014-12-26