Пара симметричных двойственных задач

Пример №1. Рассмотрим задачу “о ресурсах”:

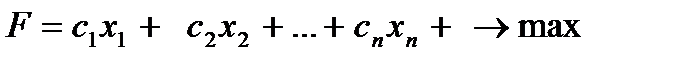
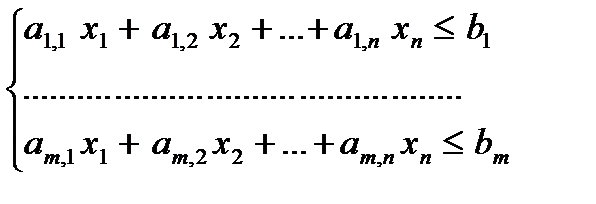(1)

.

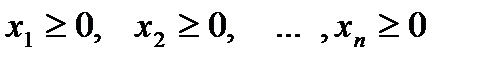Тогда двойственная задача имеет вид:

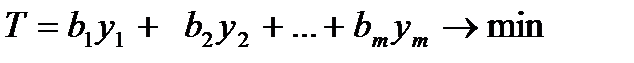
(2)

.

Заметим, что двойственная задача (2) получается из исходной задачи (1) «транспонированием», то есть заменой строк на столбцы и обратно.

Матрица системы (2) совпадает с транспонированной матрицей исходной системы (1):

.

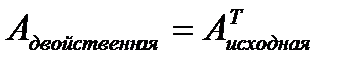Строка коэффициентов целевой функции , то есть её вектор роста совпадает с транспонированным столбцом свободных членов исходной системы (1):

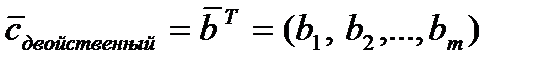^Т,

а столбец ограничений двойственной задачи совпадает с транспонированной строкой коэффициентов исходной целевой функции

.

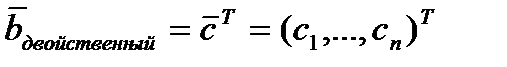Условие максимизации исходной целевой функции заменяется условием минимизации двойственной целевой функции.

Знак ограничения двойственной задачи, которое соответствует j - тому столбцу системы (1), непосредственно связан со знаком тривиального ограничения соответствующей исходной переменной 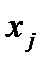. Если переменная неотрицательна 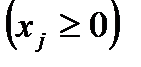и 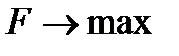, то соответствующее двойственное ограничение имеет вид:

.

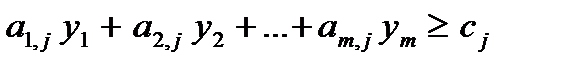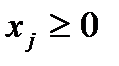Если же в исходной задаче и , то:

.

При изменении знака тривиального ограничения переменной меняется и знак соответствующего ограничения.

Чтобы определить знак тривиального ограничения для двойственной переменной по знаку соответствующего ограничения исходной задачи, можно воспользоваться тем же правилом. Для этого нужно поменять местами исходную и двойственную задачи. Если считать исходной задачу (2), то двойственной станет задача (1). Предположим, что тривиальное ограничение задачи (2) имеет вид:

,

то есть переменная y_i “имеет знак «минус»”. Поскольку целевая функция задачи (2) минимизируется (также “имеет знак «минус»”), то в задаче (1) соответствующее ограничение в этом случае должно было бы иметь вид:

,

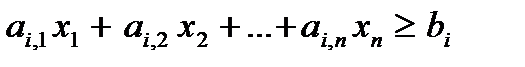(два «минуса» дают «плюс»). На самом деле это не так, поэтому тривиальное ограничение для переменной 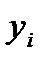имеет вид:

,

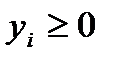то есть соответствует знаку «плюс».

Итак, по задаче (1) однозначно строится двойственная ей задача (2). Верно и обратное.

Говорят, что задачи (1) и (2) образуют пару симметричных двойственных задач. Каждая из этих задач получается из другой задачи по одним и тем же правилам, и обе являются двойственными друг другу.

Дата добавления: 2014-12-26