
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила перехода к двойственной задаче
|
|
|
|
Сформулируем теперь общие правила перехода к двойственной задаче.
1. Если в исходной задаче целевая функция максимизируется, то в двойственной задаче целевая функция минимизируется и наоборот.
2. Каждому ограничению исходной задачи соответствует переменная двойственной задачи, и каждой переменной исходной задачи соответствует ограничение двойственной задачи.
3. Компоненты вектора (строки) роста целевой функции двойственной задачи совпадают с компонентами вектора (столбца) свободных членов исходной задачи и наоборот.
4. Матрица системы нетривиальных ограничений двойственной задачи является транспонированной матрицей нетривиальных ограничений исходной задачи. Верно и обратное.
5. “Знак” ограничения двойственной задачи определяется знаком тривиального ограничения соответствующей исходной переменной и “знаком” исходной целевой функции по “правилу знаков”. Если в исходной задаче тривиальное ограничение переменной “имеет знак «плюс»” “(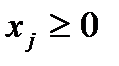 ), и целевая функция “имеет знак «плюс»”
), и целевая функция “имеет знак «плюс»”  , то и двойственное ограничение также “ имеет знак «плюс»” (то есть вид “
, то и двойственное ограничение также “ имеет знак «плюс»” (то есть вид “  ”). При изменении знака тривиального ограничения переменной исходной задачи или знака функции двойственной задачи, меняется и знак ограничения двойственной задачи. Если меняются оба знака, то знак ограничения двойственной задачи остается прежним. Если же на переменную
”). При изменении знака тривиального ограничения переменной исходной задачи или знака функции двойственной задачи, меняется и знак ограничения двойственной задачи. Если меняются оба знака, то знак ограничения двойственной задачи остается прежним. Если же на переменную 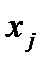 исходной задачи не накладывается тривиального ограничения, то соответствующее ограничение двойственной задачи имеет вид равенства:
исходной задачи не накладывается тривиального ограничения, то соответствующее ограничение двойственной задачи имеет вид равенства:  .
.
6. Знак тривиального ограничения двойственной задачи определяется знаком соответствующего ограничения исходной задачи и “знаком” двойственной целевой функции по тому же “правилу знаков”. Если в исходной задаче ограничение “имеет знак «плюс»” (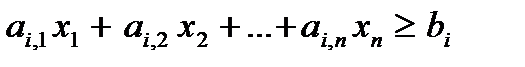 ), и целевая функция двойственной задачи “имеет знак «плюс»” (
), и целевая функция двойственной задачи “имеет знак «плюс»” (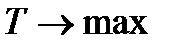 ), то и тривиальное ограничение двойственной задачи также “имеет знак «плюс»” (то есть вид
), то и тривиальное ограничение двойственной задачи также “имеет знак «плюс»” (то есть вид 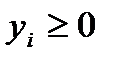 ). При изменении знака ограничения в исходной задаче или «знака» целевой функции двойственной задачи меняется и знак тривиального ограничения переменной двойственной задачи. Если меняются оба этих знака, то знак ограничения двойственной задачи остается прежним.
). При изменении знака ограничения в исходной задаче или «знака» целевой функции двойственной задачи меняется и знак тривиального ограничения переменной двойственной задачи. Если меняются оба этих знака, то знак ограничения двойственной задачи остается прежним.
Если же исходное ограничение имеет вид равенства
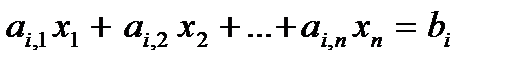 ,
,
то на соответствующую переменную 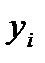 двойственной задачи не накладывается никакого тривиального ограничения.
двойственной задачи не накладывается никакого тривиального ограничения.
Замечание. Вместо применения правила 6 для определения знака тривиального ограничения двойственной задачи, можно было бы воспользоваться правилом 5, поменяв при этом исходную и двойственную задачи местами, то есть, считая двойственную задачу исходной и наоборот.
Этим замечанием мы фактически уже воспользовались, рассматривая пример 1 в 1.12.
Представим перечисленные правила в виде следующей таблицы.
Таблица 1. Правила перехода к двойственной задаче.
| № | Исходная задача | Двойственная задача |
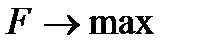
| 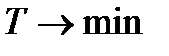
| |
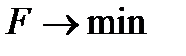
| 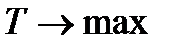
| |
| Ограничение | Переменная | |
| Переменная | Ограничение | |
Столбец свободных членов 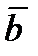
| Вектор роста
 ´ ´
| |
Вектор роста

| Столбец свободных членов 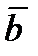 ´ ´
| |
| Матрица системы | Транспонированная матрица системы | |
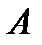
| 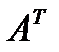
| |
| Знак переменной | «Знак» ограничения | |

| ||
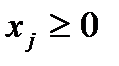
| 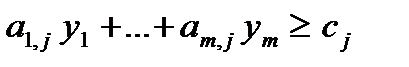
| |
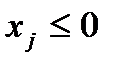
| 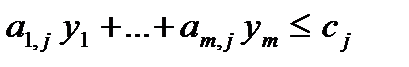
| |
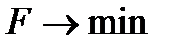
| ||
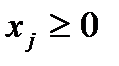
| 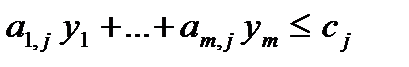
| |
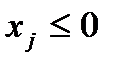
| 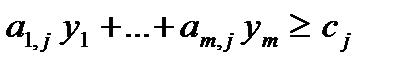
| |
| «Знак» ограничения | Знак переменной | |
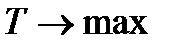
| ||
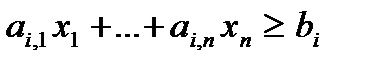
| 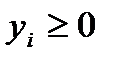
| |
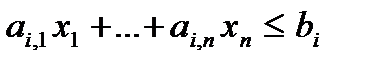
| 
| |
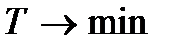
| ||
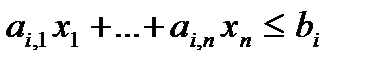
| 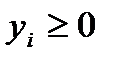
| |
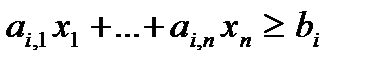
| 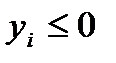
|
Отметим, что на знак переменной любой из задач влияет «знак» целевой функции той же задачи.
В заключение приведём пример перехода к задаче двойственной общей задаче линейного программирования.
Пример №1. Пусть дана исходная задача ЛП:

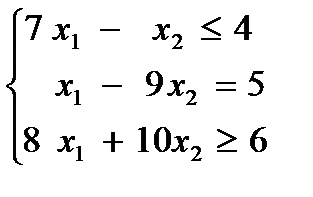 (1)
(1)

Тогда двойственная задача имеет вид:
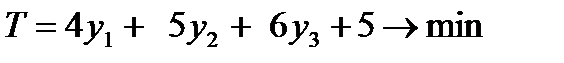
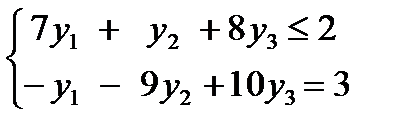 (2)
(2)

|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1691; Нарушение авторских прав?; Мы поможем в написании вашей работы!