Методы нахождения двойственных оценок

Экономический смысл двойственных оценок.

Выясним теперь экономический смысл двойственных оценок. Для удобства опять рассмотрим пару симметричных двойственных задач (1) и (2) предыдущего параграфа. Предположим, что столбец запасов ресурсов 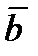изменился на величину :

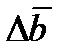, (1)

причём двойственные оценки остались прежними (при каких условиях это справедливо мы выясним ниже в п. 1.16).

Тогда для нового оптимального решения 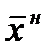по теореме двойственности справедливо равенство:

. (2)

Из (1) и (2) следует, что:

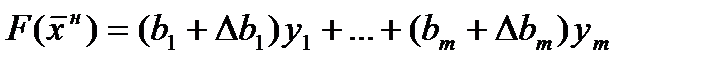. (3)

Раскрыв скобки и сгруппировав слагаемые в (3) получаем равенство:

. (4)

По теореме двойственности для старого оптимального решения 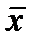справедливо равенство:

. (5)

Из (4) и (5) получаем, что

. (6)

Обозначим 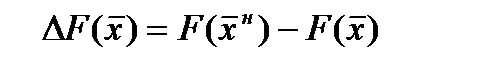изменение оптимального значения целевой функции , соответствующее изменению ресурсов 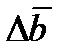. Тогда из (6) следует, что

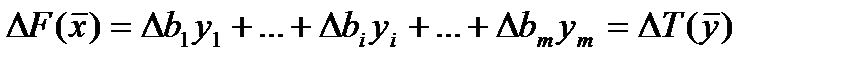. (7)

В частности при равенство (7) принимает вид:

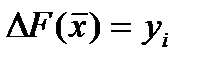. (8)

Итак, двойственная оценка 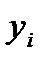численно равна изменению оптимального значения целевой функции при увеличении на единицу соответствующего запаса ресурсов .

В силу этого двойственная оценка показывает ценность ресурса. Не следует путать ценность с ценой ресурса, то есть со стоимостью единицы ресурса. Ресурс может быть дорогим, а его ценность, то есть двойственная оценка, очень малой. С другой стороны, дешёвый ресурс может оказаться ценным с точки зрения увеличения прибыли.

Пусть двойственная оценка 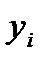равна нулю:

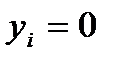. (9)

Тогда согласно (8) увеличение запаса 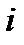-го ресурса не приводит к увеличению оптимальной прибыли . Это может объясняться только тем, что соответствующий ресурс имеется в избытке. Итак, равенство (9) говорит о том, что ресурс избыточен. Если же двойственная оценка ресурса положительна:

, (10)

то соответствующий ресурс дефицитен, поскольку согласно (8) увеличение его запаса увеличивает оптимальную прибыль.

Установив важность изучения двойственных оценок для экономического анализа задачи ЛП, укажем способ нахождения двойственных оценок. Рассмотрим следующий пример.

В п. 1.5 графическим методом найдено оптимальное решение

. (11)

однородной задачи линейного программирования

(12)

Соответствующая двойственная задача имеет вид:

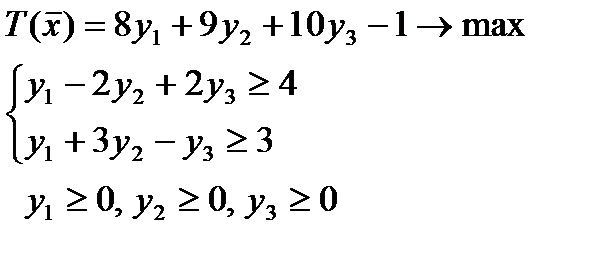(13)

Поскольку переменные оптимального решении не равны нулю, то по второй теореме двойственности получаем, что ограничения двойственной задачи выполняются для двойственных оценок в виде равенств:

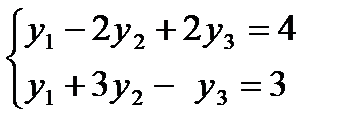(14)

Из графического решения исходной задачи (см. п.1.5, рис. 1) видно, что прямая (2) не проходит через точку C оптимального решения. Поэтому второе ограничение исходной задачи выполняется в виде строгого неравенства. По второй теореме двойственности, соответствующая двойственная оценка 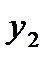равна нулю. Подставив в (14) получим систему:

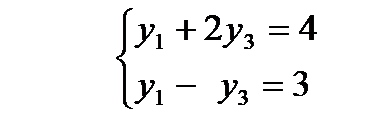(15)

Решив систему (15), находим, что:

, , (16)

и, следовательно: 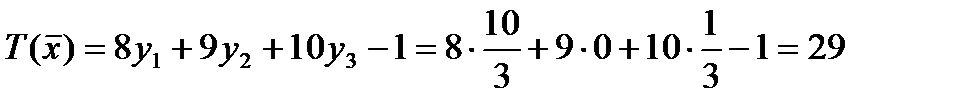(17)

Как видим, действительно выполнено равенство (12) п.1.14.

Заметим, что метод нахождения двойственных оценок с помощью второй теоремы двойственности может быть применен к любой паре двойственных задач.

Для пары симметричных двойственных задач двойственные оценки можно найти с помощью симплекс метода. Рассмотрим последнюю строку последней симплекс-таблицы (11) п.1.8, получающейся при решении рассматриваемой исходной задачи симплекс-методом:

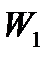
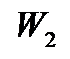
			10/3		1/3

Можно показать, что столбцы, соответствующие балансовым переменным , содержат в этой строке двойственные оценки 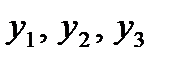. Отсюда снова получаем (16).

Дата добавления: 2014-12-26