Линейная корреляция

Работа с пропущенными значениями и выбросами.

После того, как осуществлена проверка распределения и вычислены основные описательные статистики, следует разобраться с «выбросами» и пропущенными значениями в исследуемой выборочной совокупности.

Пропущенные данные могут быть обработаны двумя способами:

1. все пропущенные значения исключаются из выборки или матрицы данных

2. пропущенные значения заменяются средними или регрессионными значениями.

Удаление пропусков может повлечь за собой ряд технических неудобств в дальнейшей обработке данных: дело в том, что ряд методов, использующих всю матрицу данных или парные данные, игнорируют все строки, в которых встречается пропущенные наблюдения.

Замена пропусков регрессионными коэффициентами более корректно, чем просто замена выборочным средним. Для этого для каждой анализируемой переменной, содержащей пропуски, выбирается парная переменная по условию максимума коэффициента корреляции (см. «Корреляционный анализ). Затем по парной переменной вычисляется линейная регрессия анализируемой переменной (см. «Регрессионный анализ»). Все пропущенные значения анализируемой переменной заменяются регрессионными, вычисленных для соответствующих значений парной переменной в качестве аргумента полученной регрессионной модели. Если парная переменная также содержит пропущенные наблюдения, то замена осуществляется по методу средних.

Описанный режим работы с пропущенными значениями поддерживают большинство статистических пакетов.

Работа с выбросами может осуществляться аналогичным образом.

Определение корреляции. Когда говорят о корреляции, используют термины корреляционной связи и корреляционной зависимости. Корреляционная связь обозначает согласованные изменения двух признаков и отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого. Прежде всего, корреляционная связь является стохастической (вероятностной) и не носит функционального характера причинно-следственных зависимостей. В корреляционных связях каждому значению одного признака может соответствовать распределение значений другого признака, но не определенное значение. Например, корреляционная связь признаков может свидетельствовать не о зависимости признаков между собой, а зависимости обоих этих признаков от какого-либо третьего или сочетания признаков, вообще не рассматриваемых в исследовании. Зависимость признаков подразумевает влияние, связь - согласованные изменения, которые могут объясняться целым комплексом причин.

Под корреляцией обычно понимается мера линейной зависимости между случайными переменными, не имеющая строгого функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой, т.е. это мера зависимости переменных, показывающая, как изменится математическое ожидание Y при изменении Х.

Числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь, называется коэффициентом корреляции.

Корреляционные связи различаются по форме, направлению и степени. По форме корреляционная связь может быть прямолинейной (шкала MAS Тейлора –шкала нейротизма Айзенка), или криволинейной (между уровнем эффективности решения задачи и мотивацией или тревожностью).

По направлению корреляционная связь может быть положительной (прямой) и отрицательной (обратной).

Степень, сила и теснота корреляционной связи определяется по величине коэффициента корреляции.

Сила связи не зависит от ее направленности и определяется по абсолютному значениюкоэффициента корреляции, принимая значения экстремума функции косинуса (от -1 до +1). Используется две системы классификации оценки силы корреляционной связи[9].

Общая классификация:

Сила связи	Значения коэффициента корреляции
сильная	r>0.70
средняя	0.50< r<0.69
умеренная	0.30< r<0.49
слабая	0.20< r<0.29
очень слабая	r<0.19

Частная классификация:

Степень достоверности	Уровень значимости
Высокая значимая корреляция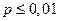
значимая корреляция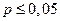
Тенденция достоверной связи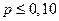
Незначимая корреляция	Ниже уровня статистической значимости

Обычно ориентируются на вторую классификацию, учитывающую объем выборки (сильная корреляция может оказаться недостоверной при малых выборках, и достоверной оказаться слабая корреляция при больших выборках, вместе с тем полагают, что сильная корреляция – это не просто корреляция высокого уровня значимости, но и с сильной теснотой связи не ниже 0,70).

В психологических исследованиях наиболее известна линейная корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.

Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.

Простая линейная корреляция (Пирсона r). Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале. Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и футах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).

Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.

Как интерпретировать значения корреляций. Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r²) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и ее значимость.

Значимость корреляций. Возникает закономерный вопрос, почему более сильные зависимости между переменными являются более значимыми? Если предполагать отсутствие зависимости между соответствующими переменными в популяции, то наиболее вероятно ожидать, что в исследуемой выборке связь между этими переменными также будет отсутствовать. Таким образом, чем более сильная зависимость обнаружена в выборке, тем менее вероятно, что этой зависимости нет в популяции, из которой она извлечена. Величина зависимости и значимость тесно связаны между собой, и можно было бы попытаться вывести значимость из величины зависимости и наоборот. Однако указанная связь между зависимостью и значимостью имеет место только при фиксированном объеме выборки, поскольку при различных объемах выборки одна и та же зависимость может оказаться как высоко значимой, так и незначимой вовсе.

Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие. Тем не менее, имеется несколько серьезных опасностей, о которых следует знать.

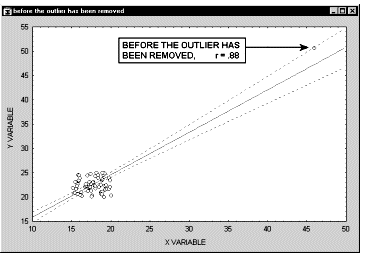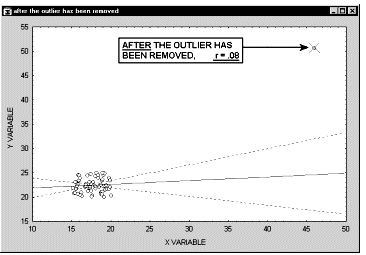
Выбросы. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.

Заметим, что если размер выборки относительно мал, то добавление или исключение некоторых данных (которые, возможно, не являются "выбросами", как в предыдущем примере) способно оказать существенное влияние на прямую регрессии (и коэффициент корреляции). Это показано в следующем примере, где мы назвали исключенные точки "выбросами"; хотя, возможно, они являются не выбросами, а экстремальными значениями.

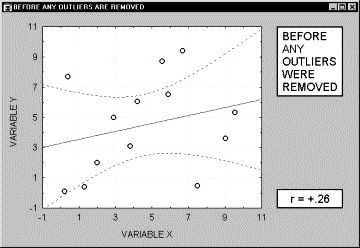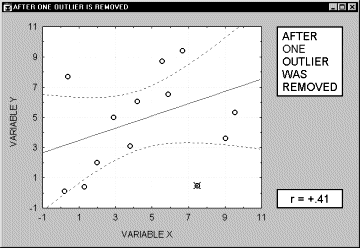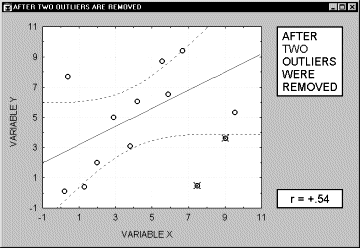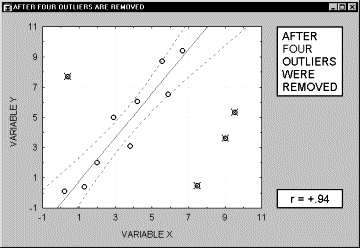
Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. К сожалению, не существует общепринятого метода автоматического удаления выбросов. Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяния каждый важный случай значимой корреляции. Очевидно, выбросы могут не только искусственно увеличить значение коэффициента корреляции, но также реально уменьшить существующую корреляцию.

Количественный подход к выбросам. Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 стандартных отклонений (и даже ±1.5 стандартных отклонений) вокруг выборочного среднего. В ряде случаев такая "чистка" данных абсолютно необходима. Например, при изучении реакции в когнитивной психологии, даже если почти все значения экспериментальных данных лежат в диапазоне 300-700 миллисекунд, то несколько "странных времен реакции" 10-15 секунд совершенно меняют общую картину. К сожалению, в общем случае, определение выбросов субъективно, и решение должно приниматься индивидуально в каждом эксперименте (с учетом особенностей эксперимента или "сложившейся практики" в данной области). Следует заметить, что в некоторых случаях относительная частота выбросов к численности групп может быть исследована и разумно проинтерпретирована с точки зрения самой организации эксперимента.

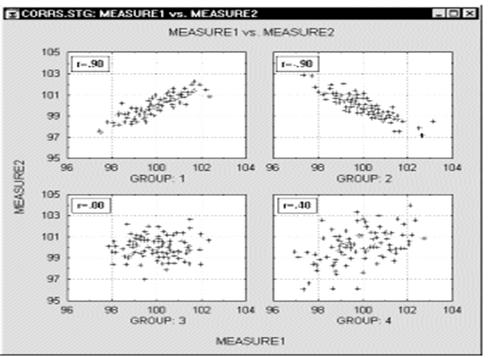
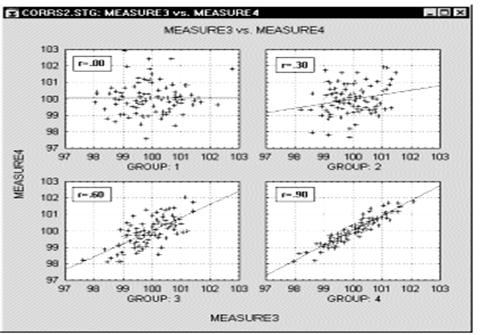
Корреляции в неоднородных группах. Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Представьте ситуацию, когда коэффициент корреляции вычислен по данным, которые поступили из двух различных экспериментальных групп, что, однако, было проигнорировано при вычислениях. Далее, пусть действия экспериментатора в одной из групп увеличивают значения обеих коррелированных величин, и, таким образом, данные каждой группы сильно различаются на диаграмме рассеяния (как показано ниже на графике).

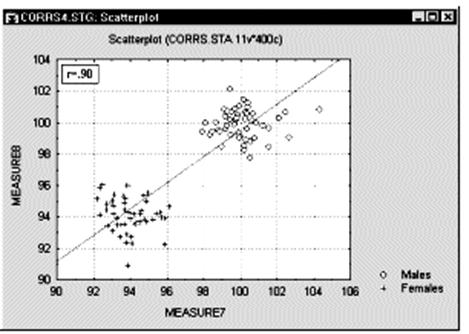
В подобных ситуациях высокая корреляция может быть следствием разбиения данных на две группы, а вовсе не отражать "истинную" зависимость между двумя переменными, которая может практически отсутствовать (это можно заметить, взглянув на каждую группу отдельно, см. следующий график).

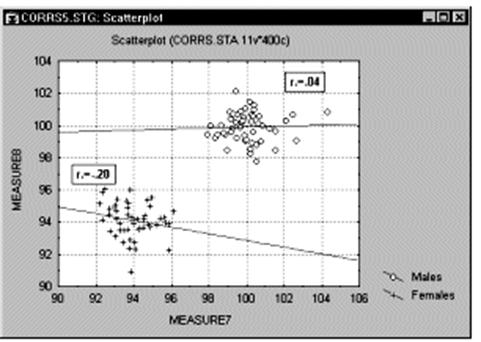
Если вы допускаете такое явление и знаете, как определить "подмножества" данных, попытайтесь вычислить корреляции отдельно для каждого множества. Если вам неясно, как определить подмножества, попытайтесь применить многомерные методы разведочного анализа.

Нелинейные зависимости между переменными. Другим возможным источником трудностей, связанным с линейной корреляцией Пирсона r, является форма зависимости. Корреляция Пирсона r хорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрения диаграммы рассеяния для каждого коэффициента корреляции, является нелинейность. Например, следующий график показывает сильную корреляцию между двумя переменными, которую невозможно хорошо описать с помощью линейной функции.

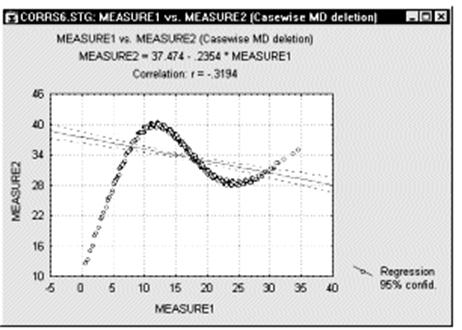
Измерение нелинейных зависимостей. Что делать, если корреляция сильная, однако зависимость явно нелинейная? К сожалению, не существует простого ответа на данный вопрос, так как не имеется естественного обобщения коэффициента корреляции Пирсона r на случай нелинейных зависимостей. Однако, если кривая монотонна (монотонно возрастает или, напротив, монотонно убывает), то можно преобразовать одну или обе переменные, чтобы сделать зависимость линейной, а затем уже вычислить корреляцию между преобразованными величинами. Для этого часто используется логарифмическое преобразование. Другой подход состоит в использовании непараметрической корреляции (например, корреляции Спирмена). Иногда этот метод приводит к успеху, хотя непараметрические корреляции чувствительны только к упорядоченным значениям переменных, например, по определению, они пренебрегают монотонными преобразованиями данных. К сожалению, два самых точных метода исследования нелинейных зависимостей непросты и требуют хорошего навыка "экспериментирования" с данными. Эти методы состоят в следующем:

Нужно попытаться найти функцию, которая наилучшим способом описывает данные. После того, как вы определили функцию, можно проверить ее "степень согласия" с данными.

Вы можете иметь дело с данными, разбитыми некоторой переменной на группы (например, на 4 или 5 групп). Определите эту переменную как группирующую переменную, а затем примените дисперсионный анализ.

Разведочный анализ корреляционных матриц. Во многих исследованиях первый шаг анализа состоит в вычислении корреляционной матрицы всех переменных и проверке значимых (ожидаемых и неожиданных) корреляций. После того как это сделано, следует понять общую природу обнаруженной статистической значимости. Иными словами, понять, почему одни коэффициенты корреляции значимы, а другие нет. Однако следует иметь в виду, если используется несколько критериев, значимые результаты могут появляться "удивительно часто", и это будет происходить чисто случайным образом. Например, коэффициент, значимый на уровне.05, будет встречаться чисто случайно один раз в каждом из 20 подвергнутых исследованию коэффициентов. Нет способа автоматически выделить "истинную" корреляцию. Поэтому следует подходить с осторожностью ко всем не предсказанным или заранее не запланированным результатам и попытаться соотнести их с другими (надежными) результатами. В конечном счете, самый убедительный способ проверки состоит в проведении повторного экспериментального исследования. Такое положение является общим для всех методов анализа, использующих "множественные сравнения и статистическую значимость".

Построчное удаление пропущенных данных в сравнении с попарным удалением. Принятый по умолчанию способ удаления пропущенных данных при вычислении корреляционной матрицы - состоит в построчном удалении наблюдений с пропусками (удаляется вся строка, в которой имеется хотя бы одно пропущенное значение). Этот способ приводит к "правильной" корреляционной матрице в том смысле, что все коэффициенты вычислены по одному и тому же множеству наблюдений. Однако если пропущенные значения распределены случайным образом в переменных, то данный метод может привести к тому, что в рассматриваемом множестве данных не останется ни одного неисключенного наблюдения (в каждой строке наблюдений встретится, по крайней мере, одно пропущенное значение). Чтобы избежать подобной ситуации, используют другой способ, называемый попарным удалением. В этом способе учитываются только пропуски в каждой выбранной паре переменных и игнорируются пропуски в других переменных. Корреляция между парой переменных вычисляется по наблюдениям, где нет пропусков. Во многих ситуациях, особенно когда число пропусков относительно мало, скажем 10%, и пропуски распределены достаточно хаотично, этот метод не приводит к серьезным ошибкам. Однако, иногда это не так.

Например, в систематическом смещении (сдвиге) оценки может "скрываться" систематическое расположение пропусков, являющееся причиной различия коэффициентов корреляции, построенных по разным подмножествам. Другая проблема связанная с корреляционной матрицей, вычисленной при попарном удалении пропусков, возникает при использовании этой матрицы в других видах анализа (например, Множественная регрессия, Факторный анализ или Кластерный анализ). В них предполагается, что используется "правильная" корреляционная матрица с определенным уровнем состоятельности и "соответствия" различных коэффициентов. Использование матрицы с "плохими" (смещенными) оценками приводит к тому, что программа либо не в состоянии анализировать такую матрицу, либо результаты будут ошибочными. Поэтому, если применяется попарный метод исключения пропущенных данных, необходимо проверить, имеются или нет систематические закономерности в распределении пропусков.

Как определить смещения, вызванные попарным удалением пропущенных данных. Если попарное исключение пропущенных данных не приводит к какому-либо систематическому сдвигу в оценках, то все эти статистики будут похожи на аналогичные статистики, вычисленные при построчном способе удаления пропусков. Если наблюдается значительное различие, то есть основание предполагать наличие сдвига в оценках. Например, если среднее (или стандартное отклонение) значений переменной A, которое использовалось при вычислении ее корреляции с переменной B, много меньше среднего (или стандартного отклонения) тех же значений переменной A, которые использовались при вычислении ее корреляции с переменной C, то имеются все основания ожидать, что эти две корреляции (A-B и A-C) основаны на разных подмножествах данных, и, таким образом, в оценках корреляций имеется сдвиг, вызванный неслучайным расположением пропусков в значениях переменных.

Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения. Другим общим методом, позволяющим избежать потери наблюдений при построчном способе удаления наблюдений с пропусками, является замена средним (для каждой переменной пропущенные значения заменяются средним значением этой переменной). Подстановка среднего вместо пропусков имеет свои преимущества и недостатки в сравнении с попарным способом удаления пропусков. Основное преимущество в том, что он дает состоятельные оценки, однако имеет следующие недостатки:

Подстановка среднегоискусственно уменьшает разброс данных, иными словами, чем больше пропусков, тем больше данных, совпадающих со средним значением, искусственно добавленным в данные.

Так как пропущенные данные заменяются искусственно созданными "средними", то корреляции могут сильно уменьшиться.

Ложные корреляции. Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными, однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями "других", остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причиненный ущерб, так и на число вызванных пожарных. Если вы будете "контролировать" эту переменную (например, рассматривать только пожары определенной величины), то исходная корреляция (между ущербом и числом пожарных) либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является ее агентом. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключенное) влияние определенных переменных.

Являются ли коэффициенты корреляции "аддитивными"? Нет, не являются. Например, усредненный коэффициент корреляции, вычисленный по нескольким выборкам, не совпадает со "средней корреляцией" во всех этих выборках. Причина в том, что коэффициент корреляции не является линейной функцией величины зависимости между переменными. Коэффициенты корреляции не могут быть просто усреднены. Если вас интересует средний коэффициент корреляции, следует преобразовать коэффициенты корреляции в такую меру зависимости, которая будет аддитивной. Например, до того, как усреднить коэффициенты корреляции, их можно возвести в квадрат, получить коэффициенты детерминации, которые уже будут аддитивными, или преобразовать корреляции в z значения Фишера, которые также аддитивны.

Как определить, являются ли два коэффициента корреляции значимо различными. Имеется критерий, позволяющий оценить значимость различия двух коэффициентов корреляциями. Результат применения критерия зависит не только от величины разности этих коэффициентов, но и от объема выборок и величины самих этих коэффициентов. В соответствии с ранее обсуждаемыми принципами, чем больше объем выборки, тем меньший эффект мы можем значимо обнаружить. Вообще говоря, в соответствии с общим принципом, надежность коэффициента корреляции увеличивается с увеличением его абсолютного значения, относительно малые различия между большими коэффициентами могут быть значимыми.

Дата добавления: 2014-12-26