Плоские графы. 1. Покажите, что графы, изображенные на рис

Упражнения

1. Покажите, что графы, изображенные на рис. 1, 2, 6, не изоморфны между собой.

2. Укажите еще одну причину, в силу которой два графа рис. 11 не могут быть изоморфными.

3. Обозначьте вершины двухграфов рис. 12 так, чтобы изоморфность этих графов стала очевидной.

Для многих целей безразлично, как именно изображен граф, т. е. изоморфные графы, доставляющие одну и ту же информацию, могут рассматриваться как один граф. Так будет, например, в том случае, с которого начато изложение, – когда граф играет роль своеобразного списка уже проведенных игр. Однако в других случаях существенно то обстоятельство, что граф может быть начерчен некоторым специальным образом. Сравним два изоморфных графа, изображенные на рис. 1 и 7. На первом из них ребра пересекаются в пяти точках, не являющихся вершинами графа, на втором все точки пересечения ребер графа служат его вершинами.

Граф, который можно начертить таким образом, чтобы его ребра пересекались только в вершинах, называется плоским графом. Так, граф G, изображенный на рис. 1, является плоским, потому что существует изоморфный ему граф (рис. 7), все ребра которого пересекаются только в вершинах.

Плоский граф можно рассматривать как карту дорог, соединяющих между собой различные станции или деревни. Так, на карте, изображенной на рис. 13, мы видим 7 станций: А, В,..., G, причем некоторые из них соединены друг с другом дорогами: АG, ВС, FE и т. д., и обратно, каждую карту дорог можно рассматривать как плоский граф. План любого города тоже является плоским графом, где улицы служат ребрами, а площади и уличные перекрестки – вершинами.

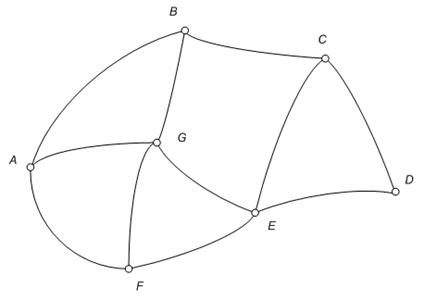
Рис. 13. Граф, соответствующий карте дорог, соединяющих семь станций

Впрочем, современная техника изменила многие наши представления, и, чтобы не отстать от современных требований, необходимо признать, что и карта дорог в настоящее время уже не всегда представляетсяплоским графом. К сети дорог теперь часто добавляются линии, проходящие на разных уровнях (дорожные развязки), так что в месте пересечения двух дорог пассажир не может перейти с одной линии на другую (рис. 14).

Рис. 14. Фотография современной многоуровневой дорожной развязки, которую невозможно представить плоским графом

Иными словами, ребра графа такой карты пересекаются в точках, которые нельзя считать вершинами графа.

Планарным называется граф, изоморфный плоскому графу. Иначе говоря, граф планарный, если существует возможность получения плоской укладки такого графа.

В дополнение к перечисленным выше представлениям графа укажем еще одно приложение плоских графов к важной задаче практики: его можно рассматривать как схему электрической сети, где ребрами служат провода, соединяющие различные пункты. Один из наиболее эффективных способов массового производства стандартных электрических схем для радио- и телевизионных приемников состоит в том, что схема наносится печатным способом в виде металлической фольги на бумажную или пластмассовую основу. Однако для того, чтобы это было осуществимо, граф рассматриваемой сети проводов должен иметь плоское представление; ведь пересечение двух ребер привело бы к короткому замыканию в системе.

Дата добавления: 2014-12-27