Нуль-граф и полный граф

Упражнения

1. Начертите граф игр, сыгранных к середине сезона вашими футбольными или волейбольными командами.

2. Дайте полный список проведенных игр, соответствующий графу рис. 2.

3. Сколько ребер и сколько вершин имеют графы рис. 1 и 2?

Существуют некоторые специальные графы, встречающиеся во многих приложениях теории графов. Будем пока опять рассматривать граф как наглядную схему,иллюстрирующую ход спортивных состязаний. Доначала сезона, пока еще никакие игры не проводились, на графе нет никаких ребер. Такой граф состоит из одних изолированных вершин, т. е. извершин, не соединенных никакими ребрами. Граф такого вида называется нуль-графом. На рис. 3приведены такие графы для случаев, когда число команд, или вершин, равно 1, 2, 3, 4 и 5. Эти нуль-графы обычно обозначаются символами O₁, O₂, O₃ и т. д., такчто O_n – это нуль-граф с n вершинами, не имеющий ребер.

Рассмотрим другой крайний случай. Предположим, что по окончании сезона каждая команда сыграла по одному разу с каждой из остальных команд. Тогда на соответствующем графе каждая пара вершин будет соединена ребром. Такой граф называется полным графом. На рис. 4 изображены полные графы с числом вершин n = l, 2, 3, 4, 5.

Рис. 3. Нуль-графы для различного числа команд: 1,2,3,4 и 5

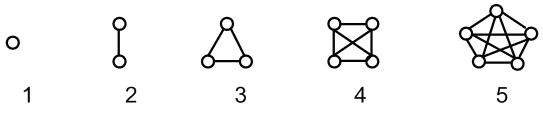
Рис. 4. Полные графы для различного числа команд: 1,2,3,4 и 5

Обозначим этиполные графы соответственно через U₁, U₂, U₃, U₄, U₅, так что граф U_n состоит из n вершин и ребер, соединяющих все возможные пары этих вершин. Этот граф можно представлять себе как n -угольник, в котором проведены все диагонали.

Имея некоторый граф, например граф G, изображенный на рис. 1, всегда можно превратить его в полный граф с теми же самыми вершинами, добавив недостающие ребра (т. е. ребра, соответствующие играм, которые только еще будут сыграны). На рис. 5 это сделано для графа, представленного на рис. 1 (еще не состоявшиеся игры изображены пунктиром).

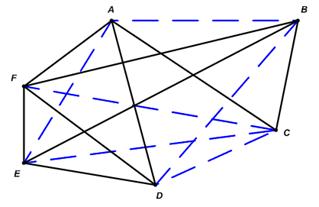
Рис. 5. Граф с рис. 1, дополненный ребрами до полного графа

Можно также отдельно начертить граф, соответствующий пока еще не сыгранным, будущим играм. Для графа G при этом получится граф, изображенный на рис. 6.

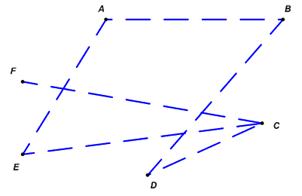
Рис. 6. Граф 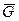, являющийся дополнением графа G с рис. 1 до полного графа

Этот новый граф называется дополнением графа G; принято обозначать его через 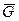. Взяв дополнение графа 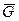, мы снова получим граф G. Ребра обоих графов G и 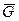вместе составляют полный граф с теми же вершинами.

Дата добавления: 2014-12-27