Определители

Определители существуют только для квадратных матриц.

В общем случае используется разложение Лапласа определителя n порядка по элементам строки (столбца) на сумму n определителей (n– 1 ) порядка.

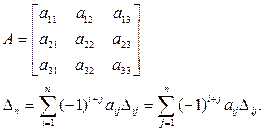
Например, для n = 3:

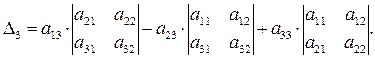
Свойства определителей

1. Определитель равен единице, если матрица А – единичная.

2. Определитель равен нулю, либо если все элементы матрицы равны нулю, либо все элементы строки (или столбца) равны нулю, или равны между собой или пропорциональны элементы произвольных двух строк (или двух столбцов).

3. Величина определителя остается неизменной по модулю при перестановке местами его строк (или столбцов).

4. Знак определителя изменяется на противоположный при замени местами его двух строк (или столбцов).

5. Значение определителя умножается на постоянную k, если все элементы какой-либо его строки (столбца) умножаются на k.

6. Значение определителя не изменяется, если к какой-либо его строке (или столбцу) прибавить умноженные на k соответствующие элементы другой строки (или столбца).

Дата добавления: 2014-12-27