Подобие насосов

При проектировании новых насосов используются:

- расчетно-теоретические разработки конструкций их проточной части;

- опытные данные испытаний в лабораторных и натурных условиях;

- опытные данные, получаемые в процессе эксплуатации аналогичных насосов.

Распространение полученных результатов исследований рабочих режимов на моделях и распространение полученных результатов на натурные насосы возможно на основе теории о механическом подобии движения реальной жидкости.

Главное положение этой теории заключается в необходимости выполнения условий геометрического, кинематического и динамического подобия.

Геометрическое подобие в гидромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток.

Два насоса могут быть названы подобными, если все линейные размеры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура).

Математически геометрическое подобие сравниваемых насосов определяется постоянством линейного коэффициента подобия:

,

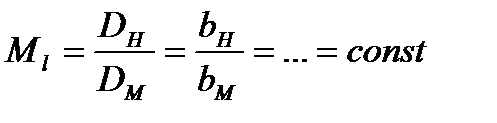где 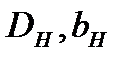и 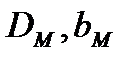- соответственно диаметр и высота рабочих колес натурного и модельного насосов.

Геометрическое подобие означает также постоянство отношений любых других размеров у модели и у натуры:

.

Для полного соблюдения геометрического подобия необходимо подобие шероховатостей обтекаемых потоком поверхностей и зазоров между движущимися и неподвижными деталями насосов, т. е. необходимо, чтобы относительные шероховатости и относительные зазоры 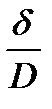были одинаковыми.

Кинематическое подобие в общем виде означает, что безразмерные поля скоростей в рассматриваемых потоках должны быть одинаковы, т. е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траектории движения в сравниваемых гидравлических системах – геометрически подобны.

Применительно к насосам это, в частности означает подобие параллелограммов скоростей в соответствующих точках потока во всех элементах проточной части двух геометрически подобных машин, работающих в одинаковых режимах.

Математически условия кинематического подобия могут быть выражены в виде ряда отношений:

.

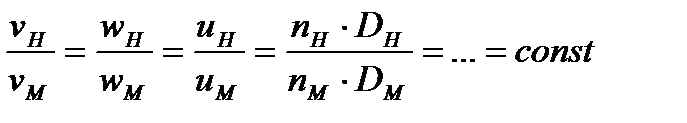Для соблюдения требований кинематического подобия необходимо также выдерживать постоянным отношение скорости протекания жидкости к скорости движения вращающихся деталей, т. е.

.

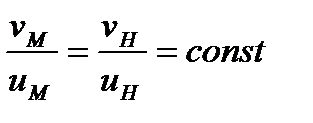Используя геометрическое подобие, из которого следует, что

1. ;

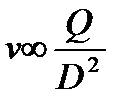2. ,

получаем еще одно условие кинематического подобия, представляющее чрезвычайно большой практический интерес при моделировании насосов:

.

Динамическое подобие кроме соблюдения условий геометрического и кинематического подобия означает пропорциональность сил, действующих в соответствующих точках потока.

При отнесении к этим силам сил:

- давления;

- вязкости;

- тяжести;

- инерции

динамическое подобие в общем виде обуславливается равенством чисел:

- Эйлера;

- Рейнольдса;

- Фруда;

- Струхаля.

;

;

;

,

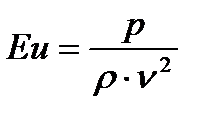где 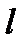- характерный линейный размер;

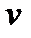- кинематическая вязкость жидкости;

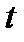- время.

Все эти критерии являются определяющими лишь тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях.

Дата добавления: 2014-12-27