
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент быстроходности насоса
|
|
|
|
Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вращения. Естественно, что конструкция рабочих колес и всех элементов проточной части насоса, равно как и их размеры, при этом меняются.
Для сравнения лопастных насосов различных типов пользуются коэффициентом быстроходности, объединяя группы рабочих колес по принципу их геометрического и кинематического подобия.
Коэффициентом быстроходности 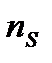 насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.
насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.
Численное значение коэффициента быстроходности можно определить, воспользовавшись формулами пересчета для однотипных насосов с рабочими колесами различных диаметров, работающих с переменной частотой вращения:
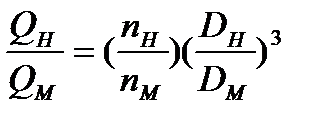 ;
;
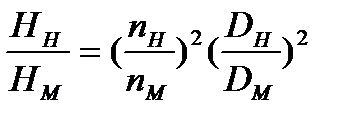 ;
;
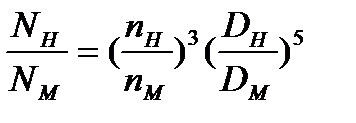 .
.
Применив эти формулы к данному насосу и геометрически подобному ему с рабочим колесом диаметром 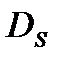 и частотой вращения
и частотой вращения 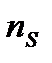 , получим:
, получим:
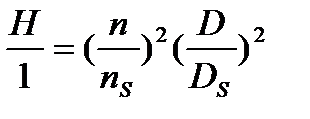 ;
;
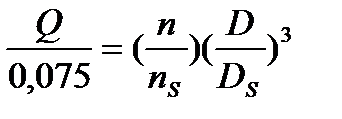 .
.
Исключив из этих выражений отношение 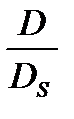 , найдем:
, найдем:
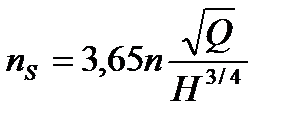 . (1*)
. (1*)
Для насосов двухстороннего входа вместо 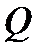 следует принимать
следует принимать 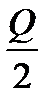 .
.
Подставив вместо подачи 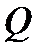 ее значение из формулы:
ее значение из формулы: 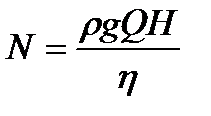

для насосов, перекачивающих воду 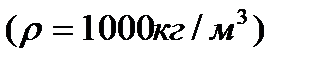 , получим другую формулу для определения коэффициента быстроходности:
, получим другую формулу для определения коэффициента быстроходности:
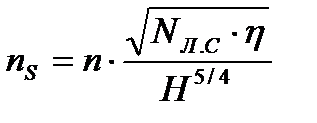 , (2*)
, (2*)
где  - мощность насоса в лошадиных силах.
- мощность насоса в лошадиных силах.
Значение коэффициента быстроходности изменяется в широком диапазоне:
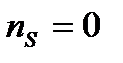 при
при 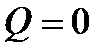 ;
;
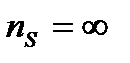 при
при 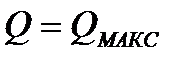 и
и 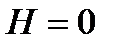 .
.
Для внесения определенности в понятие коэффициента быстроходности условились в формулы (1*) и (2*) подставлять оптимальные по КПД значения мощности, подачи и напора.
Из формулы (1*) вытекает, что:
- с увеличением напора коэффициент быстроходности насоса уменьшается;
- увеличение подачи приводит при прочих равных условиях к повышению коэффициента быстроходности.
Следовательно, тихоходные насосы (насосы с малым коэффициентом быстроходности) – это насосы, имеющие большой напор и сравнительно небольшую подачу.
Быстроходные насосы – насосы, имеющие меньший напор, но большую подачу.
Коэффициент быстроходности является очень важным удельным показателем, который широко используется в качестве характеристики типа насоса. Он одновременно учитывает три наиболее существенных параметра любого насоса:
- частоту вращения;
- мощность (или подачу);
- напор.
Значение коэффициента быстроходности в известной степени определяет и форму рабочего колеса.
Для тихоходных центробежных насосов: 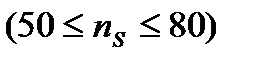
- большой напор создается за счет увеличения диаметра рабочего колеса на выходе 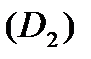 ;
;
- небольшая подача обуславливается малой высотой рабочего колеса у выхода 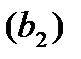 и малым его диаметром на входе
и малым его диаметром на входе 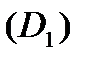 .
.
Поэтому тихоходные колеса имеют большие значения 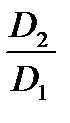 и малые значения
и малые значения 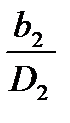 .
.
С увеличением быстроходности разница между выходным и входным диаметрами сокращается, а высота возрастает.
Коэффициент быстроходности пропорционален частоте вращения.
Повышение частоты вращения, как правило, ведет к уменьшению размеров и массы насоса и приводного двигателя.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 7187; Нарушение авторских прав?; Мы поможем в написании вашей работы!