Изменение характеристик насосов при изменении частоты вращения рабочего колеса

При необходимости пересчета паспортных характеристик, установленных при частоте вращения 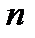на другую частоту вращения рабочего колеса 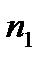при , то можно воспользоваться следующими выражениями, полученные из закона подобия центробежных насосов:

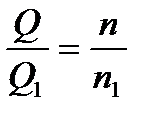; (19-1)

; (19-2)

. (19-3)

Приведенные выше выражения называются законом пропорциональности.

;

;

.

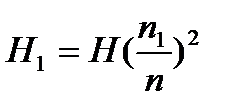Высота всасывания насоса при работе его с частотой вращения 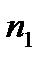определяется по уравнению:

,

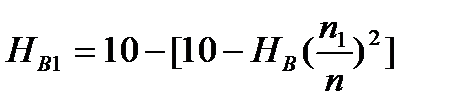где 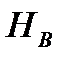и 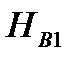- допускаемая вакуумметрическая высота всасывания при частотах вращения 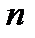и .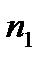

Установленный закон пропорциональности позволяет по одной опытной характеристике построить ряд характеристик насоса в широком диапазоне изменения частоты вращения.

Необходимо отметить, что режим работы насоса с пониженной частотой вращения допускается всегда, но повышение частоты вращения больше чем на 10 – 15 % должно быть согласовано с заводом-изготовителем.

Исключая из уравнений (19-1) и (19-2) частоту вращения, получим:

и ,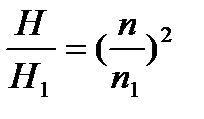

откуда: 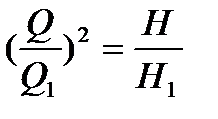, откуда: .

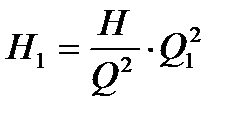Таким образом, получено уравнение параболы с вершиной в начале координат, проходящей через точку А, принадлежащую кривой 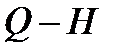и имеющую координаты 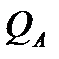и .

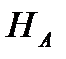Парабола ОА_i – A₂ – A₁ – A представляет собой геометрическое место точек, определяющих режимы насоса, подобных режиму в точке А, и называется параболой подобных режимов.

Пересчет координат точки А по закону пропорциональности для любой другой частоты вращения приведет к точкам на параболе подобных режимов.

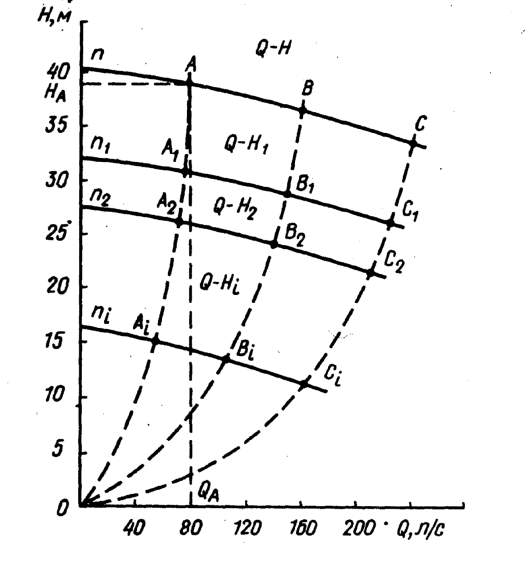
Пересчет всякой другой точки В, С, … характеристики 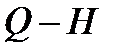построенной при частоте вращения 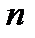на частоту 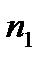, , … 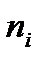даст точки , , 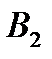… ; , , 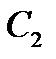… 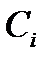и так далее, которые расположатся соответственно на параболах ; .

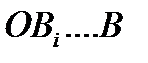Соединяя точки плавной кривой, получаем характеристику 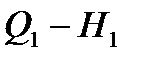насоса для частоты вращения .

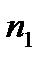Для характеристик … построения будут аналогичными.

Теоретически параболы подобных режимов являются линиями постоянного КПД.

В действительности насос не сохраняет постоянство КПД. Это связано с тем, что при изменении частоты вращения в разной степени и с разной интенсивностью проявляются потери мощности насоса (механические, объемные, гидравлические).

Отмечая на полученных характеристиках , 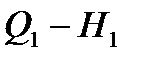… точки с равными значениями КПД и соединяя их плавными кривыми, получаем так называемую универсальную характеристику.

Из которой видно, что максимальное значение КПД обеспечивают двигатели с частотой вращения 1450 мин^-1.

1.20. ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК НАСОСОВ ПРИ ИЗМЕНЕНИИ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ РАБОЧЕГО КОЛЕСА

Требования потребителей по подаче и напору чрезвычайно разнообразны, поэтому экономически нецелесообразно изготовлять насосы для каждого расчетного случая.

Для увеличения области применения насоса в практике проектирования и эксплуатации насосных станций применяют срезку рабочего колеса насоса, т. е. уменьшают диаметр рабочего колеса по внешнему обводу 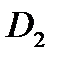, сохраняя .

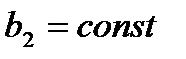Подачу 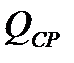и напор насоса, имеющего срезанное рабочее колесо диаметром , можно определить по уравнениям закона подобия центробежных насосов:

; ; ,

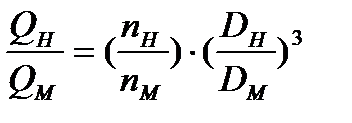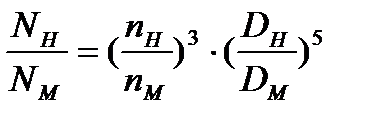зная подачу 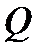и напор 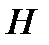насоса при номинальном (не срезанном) рабочем колесе диаметром .

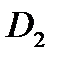Из закона подобия при условии, что частота вращения 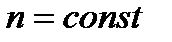и ширина колеса 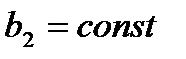, получим:

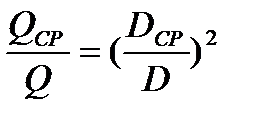, (20.1)

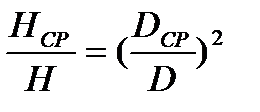. (20.1)

Экспериментальная проверка полученных равенств показывает, что для центробежных насосов, имеющих коэффициент быстроходности , лучшее соответствие расчетных величин 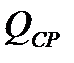и опытным данным получается при расчете величины срезки колеса по формулам:

, (20.2)

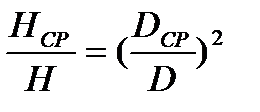, (20.2)

откуда: , .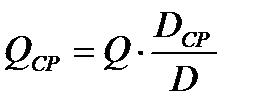

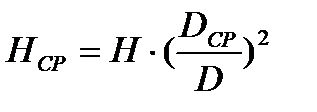Для исследования положения режимных точек работы насоса при срезке рабочего колеса насоса рассмотрим уравнения (20.1).

Из уравнений следует, что:

, ,

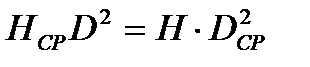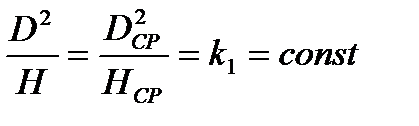
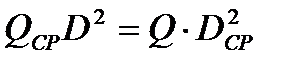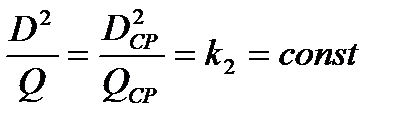
Откуда: 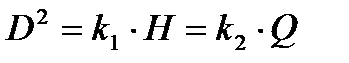, или .

Выражая отношение коэффициентов через: 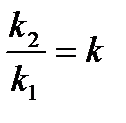, получим:

.

Следовательно, перемещение режимных точек в координатах при уменьшении диаметра рабочего колеса насоса происходит по прямым линиям (I), проходящим через начало координат. Таким образом точка 1 с параметрами и перемещается в положение 2 с параметрами и .

Проведем аналогичные исследования равенств (20.2):

.

.

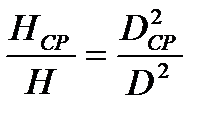
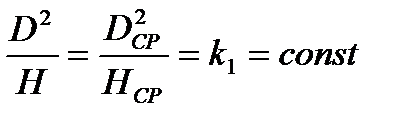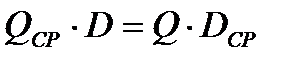
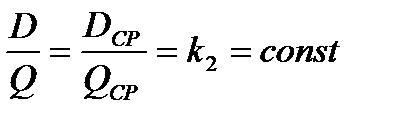
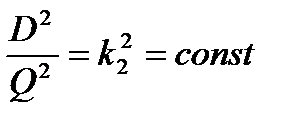Откуда: 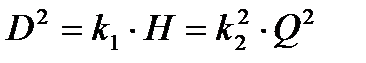, или

Выражая отношение коэффициентов через: , получим:

.

Таким образом, при расчете срезки рабочего колеса по уравнениям (20.2) режимные точки перемещаются по квадратичным параболам (II) с вершинами в начале координат, т. е. точка 1 при срезке колеса перемещается в положение 3.

Изменение КПД насоса можно рассчитать по формуле Муди:

.

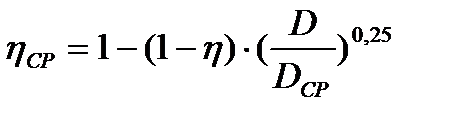Экспериментальное исследование 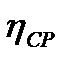показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности.

С достаточной степенью точности можно принять, что КПД насоса уменьшается на 1% на каждые 10% срезки колеса с коэффициентом быстроходности и на 1% на каждые 4% срезки при .

В зависимости от коэффициента быстроходности рекомендуются следующие пределы срезки колес:

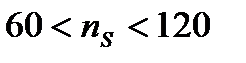...... 20 – 15%

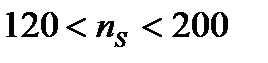..... 15 – 11%

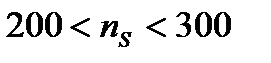..... 11 – 7 %

Оптимальный КПД насоса соответствует его расчетным подаче 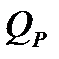и напору , поэтому насос следует подбирать таким образом, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного режима работы, составляли не более 5 – 10% от максимального КПД.

Пространство, заключенное между характеристиками при номинальном размере колеса и 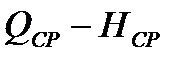при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими подачам в пределах рекомендуемых отклонений КПД, называется полем насоса – рекомендуемой областью применения насоса.

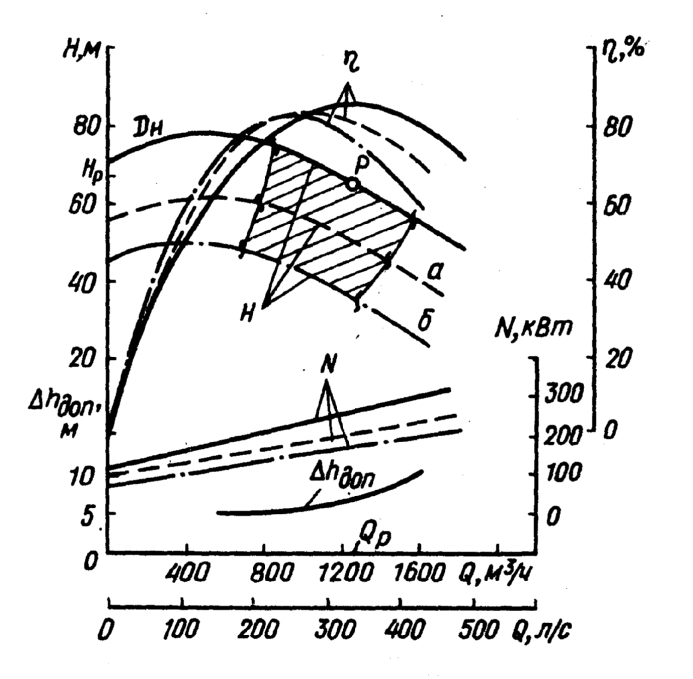
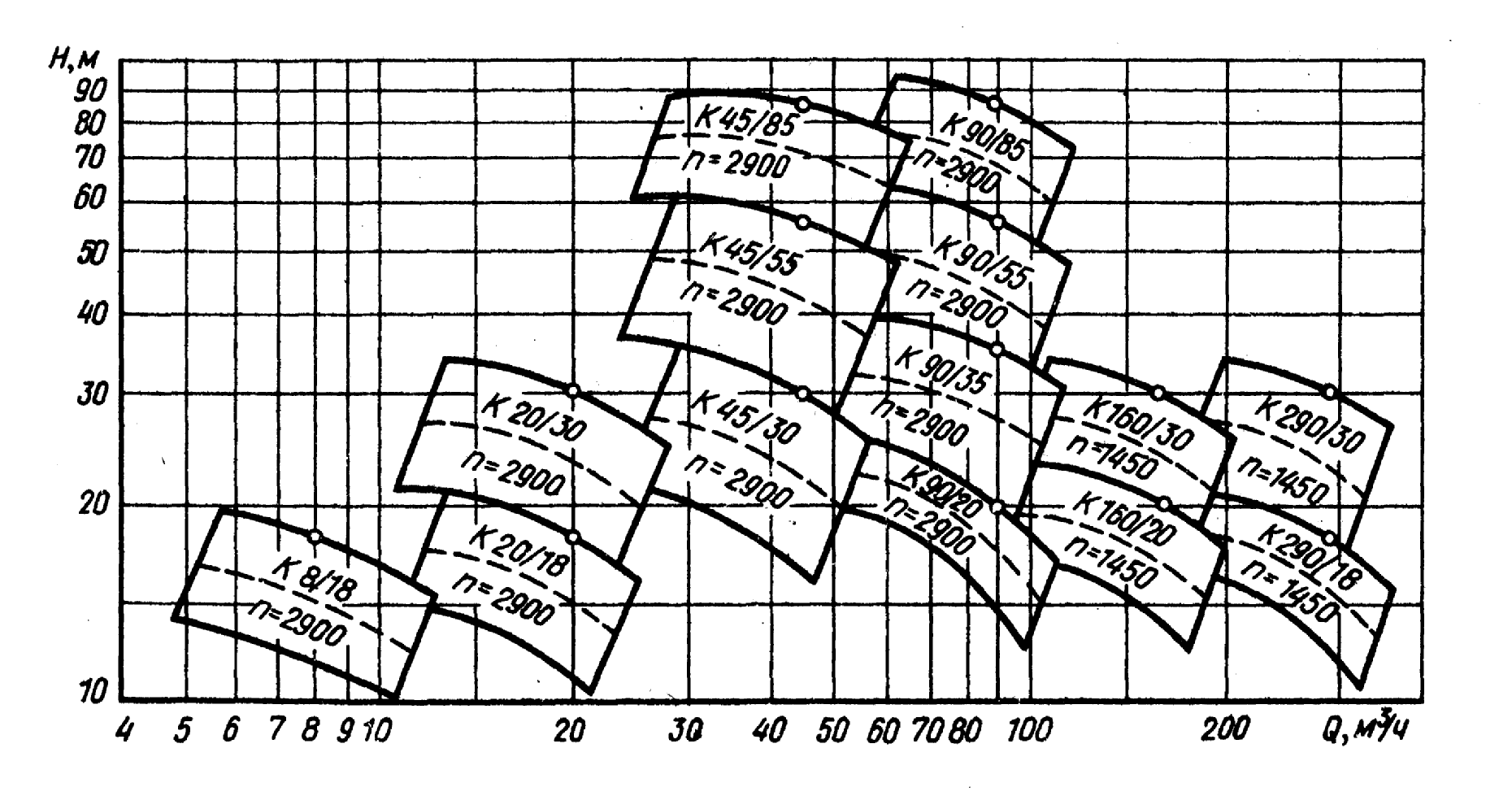
В каталогах-справочниках приводятся сводные графики полей насосов. По этим графикам удобно подбирать насос на заданный режим работы.

Сводный график полей насосов типа К приведен на рисунке:

Дата добавления: 2014-12-27