Способы получения характеристик насосов

При расчете режима насоса, как правило, пользуются опытными характеристиками, которые получают при испытании насосов.

При проведении опытных испытаний осуществляют измерения:

- подачи насоса;

- напора насоса на входе и выходе из него;

- потребляемой мощности насоса;

- вакуумметрической высоты всасывания насоса.

По результатам измерений вычисляют:

- напор, приведенный к оси насоса;

- полезную мощность при постоянной частоте вращения;

- КПД при постоянной частоте вращения.

Полученные значения напора, мощности, КПД и допустимого кавитационного запаса для ряда значений подачи представляют в виде системы точек в координатах: H, N, h, Dh_ДОП и Q.

Соединяя соответствующие точки плавными линиями, получают графически выраженные зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения для данного диаметра рабочего колеса.

Полученные кривые: 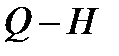, , 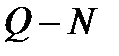, 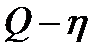называются энергетическими характеристиками центробежного насоса и вписываются в паспорт насоса.

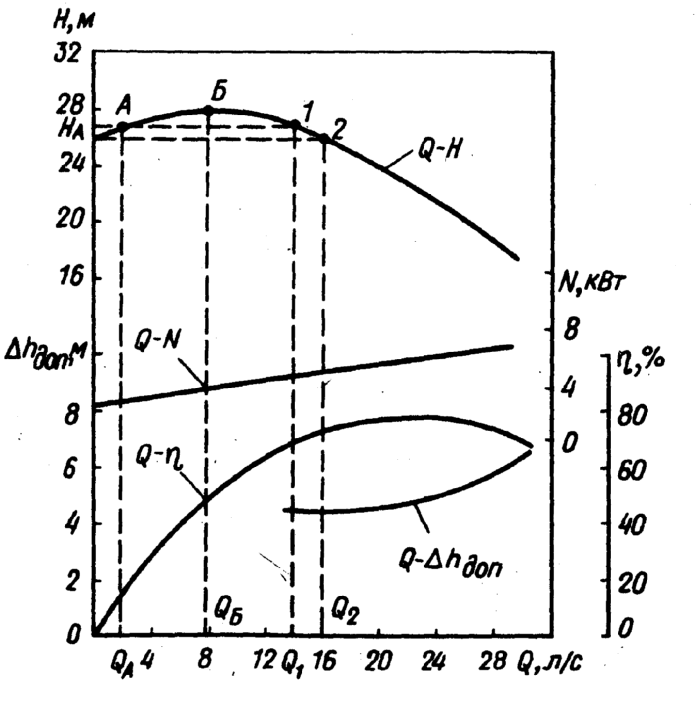
Рабочие характеристики центробежного насоса представлены на рисунке:

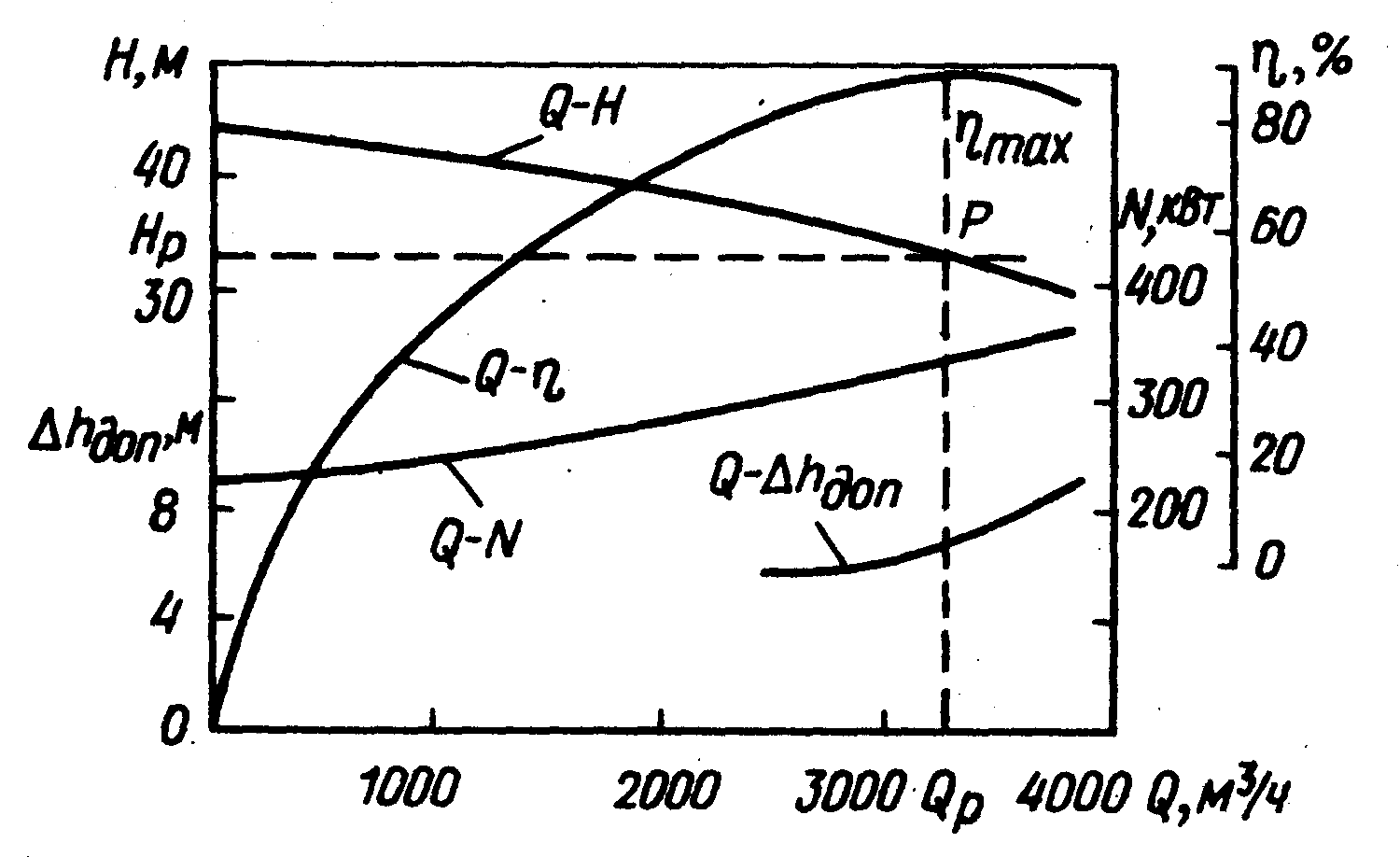
Максимальному значению КПД соответствует подача 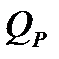и напор 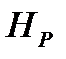(расчетные параметры).

Точка Р характеристики 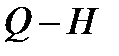, отвечающая максимальному значению КПД, называется оптимальной режимной точкой.

Характеристика 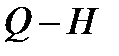показывает, что с уменьшением подачи напор возрастает и при подаче, равной нулю, т. е. при закрытой задвижке на напорном трубопроводе, достигает максимального значения. Данная характеристика 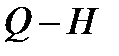называется стабильной (характеристика, не имеющая возрастающей ветви).

Режим работы насоса, имеющего стабильную рабочую характеристику 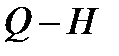, протекает устойчиво во всех точках кривой.

Характеристика 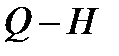насоса, в соответствии с которой, напор возрастает при начальном увеличении подачи, а затем падает, называется восходящей.

Восходящая характеристика 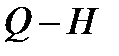представлена на рисунке:

Графическая характеристика имеет восходящую ветвь от 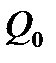до .

Напору 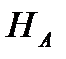соответствуют две подач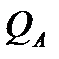и и . Изменение подачи насоса наступает внезапно, сопровождается сильным шумом и гидравлическими ударами.

Работа насоса в пределах подачи от нуля до называется областью неустойчивой работы.

Форма характеристики 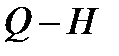зависит от коэффициента быстроходности насоса 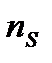. Чем больше коэффициент быстроходности, тем круче кривая .

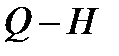Насосы со стабильными пологими характеристиками целесообразно применять в системах, где при постоянном напоре требуется регулирование подачи в широких пределах.

Насосы со стабильными крутопадающими характеристиками целесообразно применять в системах со значительными колебаниями напора при необходимости сохранения по возможности постоянной подачи.

Насосы с восходящими характеристиками рекомендуется применять в системах, где подача не снижается до (до подачи, соответствующей напору при закрытой задвижке).

Дата добавления: 2014-12-27