Объемные потери одноступенчатого насоса

Жидкость, выходящая из рабочего колеса в количестве Q_К в основном поступает в отвод и затем в нагнетательный патрубок насоса и частично возвращается в подвод через зазоры в уплотнении между рабочим колесом и корпусом насоса (утечка q_К). Энергия жидкости, возвращающейся в подвод, теряется. Эти потери называются объемными. Утечки обусловлены тем, что давление на выходе из рабочего колеса больше, чем в подводе. Утечки тем больше, чем больше зазор в уплотнении между рабочим колесом и корпусом насоса.

Схема образования объемных потерь в уплотнении рабочего колеса представлена на рисунке:

Кроме рассмотренных утечек жидкости, имеет место утечки через сальники, но эти утечки весьма малы, и при рассмотрении баланса мощности ими можно пренебречь.

Объемные потери оценивают объемным к. п. д., равным отношению мощности N^¢, оставшейся за вычетом объемных потерь, к гидравлической мощности N_Г:

.

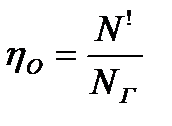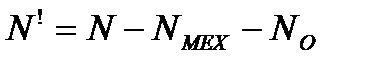
К. п. д. объемных потерь может быть определен по формуле:

.

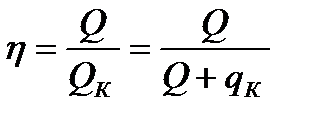Гидравлические потери

Гидравлические потери – потери на преодоление гидравлического сопротивления в:

- подводе;

- рабочем колесе;

- отводе.

Гидравлические потери оцениваются гидравлическим к. п. д., который равен отношению полезной мощности насоса N_П к мощности N^¢:

.

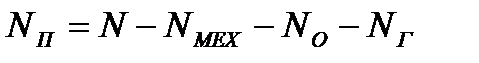
К. п. д. насоса равен:

.

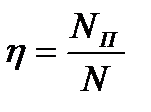Умножив и разделив правую часть этого уравнения на N_Г N^¢ и проведя перегруппировку членов, получим:

,

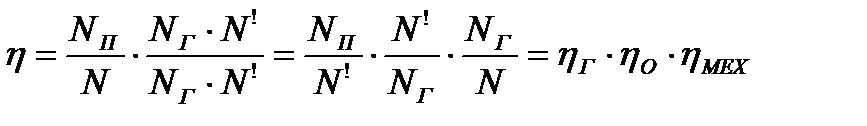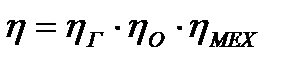
КПД насоса представляет собой произведение механического, объемного и гидравлического коэффициентов полезного действия.

КПД насоса определяет степень совершенства его конструкции, как в механическом, так и в гидравлическом отношении.

У современных насосов ; ; .

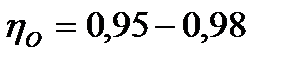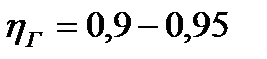Значение для каждого насоса меняется от режима работы. Максимальные значения КПД серийно выпускаемых крупных наосов достигают 0,9 – 0,92, малых – 0,6 – 0,75.

1.10. КИНЕМАТИКА ДВИЖЕНИЯ ЖИДКОСТИ В РАБОЧЕМ КОЛЕСЕ ОДНОСТУПЕНЧАТОГО ЦЕНТРОБЕЖНОГО НАСОСА

Рабочее колесо центробежных насосов является основным элементом насоса.

С помощью рабочего колеса осуществляется преобразование подводимой к насосу механической энергии в энергию движущейся жидкости. Такое преобразование происходит за счет непосредственного силового воздействия лопастей рабочего колеса на жидкость, заполняющую его каналы.

Кинематическими показателями движущейся через колесо жидкости являются:

- значения и направления скоростей;

- траектории движения жидкости.

Кинематические характеристики оказывают решающее влияние на энергетические параметры насоса (напор, подача, КПД).

Абсолютная скорость в области лопастного колеса может быть получена как геометрическая сумма двух скоростей:

- относительной ;

- переносной u.

В векторной форме: .

Параллелограмм скоростей потока в рабочем колесе центробежного насоса показан на рисунке:

Для определения составляющих абсолютной скорости рассматриваются упрощенные теоретические схемы течения жидкости в межлопастных каналах рабочего колеса центробежного насоса.

В основу представления об установившемся движении потока через рабочее колесо центробежного насоса положена гипотеза о струйном течении жидкости. Согласно этой гипотезе траектория каждой частицы жидкости в пределах межлопастного канала колеса по форме совпадает с кривой очертания лопасти.

Реально такое движение может наблюдаться лишь при бесконечно большом числе бесконечно тонких лопастей.

Тем не менее, при расчете проточной части центробежных колес с часто расположенными лопастями, образующими каналы большой длины (по сравнению с размерами поперечного сечения), такое допущение в первом приближении является вполне обоснованным.

Для определения значения и направления относительной скорости предположим, что заданы:

- геометрические размеры рабочего колеса r;

- объемная подача рабочего колеса Q;

- частота вращения рабочего колеса n.

Рассмотрим плоское сечение канала рабочего колеса. Это сечение располагается перпендикулярно оси насоса. Рассматриваемая точка потока отстоит от оси вращения на расстоянии r.

Относительная скорость в этом случае направлена по касательной к поверхности лопасти.

Для определения ее значения воспользуемся уравнением неразрывности, составив его для цилиндрического сечения потока, проходящего через рассматриваемую точку. Площадь этого сечения, за вычетом части, занятой толщиной лопастей, обозначим через .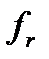

Радиальная составляющая относительной скорости потока равна:

.

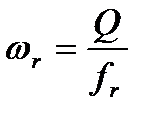Учитывая коэффициентом 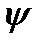степень стеснения сечения телом лопастей шириной , получим:

,

.

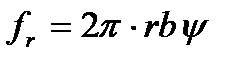Переносная скорость в рассматриваемой точке потока равна:

.

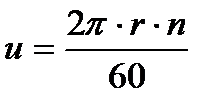Она направлена по касательной к окружности радиусом 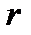в сторону вращения.

Радиальная составляющая относительной скорости лежит в рассматриваемой плоскости и перпендикулярна вектору переносной скорости u.

Касательная к поверхности лопасти, по которой направлена относительная скорость 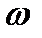, образует угол с направлением, обратным переносной скорости.

Проводя из конца вектора прямую, параллельную направлению скорости u, до пересечения с этой касательной, получим, согласно плану скоростей, в точке пересечения конец вектора относительной скорости .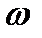

Значение относительной скорости равно:

.

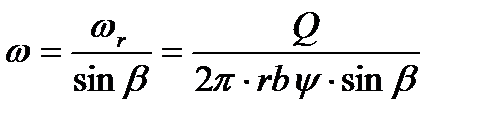Суммируя по правилу параллелограмма векторы скоростей 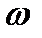и u, получаем абсолютную скорость v.

Так как радиальная составляющая относительной скорости равна радиальной составляющей 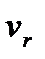абсолютной скорости, то значение скорости v может быть определено из соотношения:

,

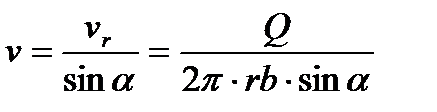где угол между направлениями скоростей (абсолютной и переносной).

Таким образом, гипотеза о струйном течении, основанная на предположении о бесконечном числе лопастей, позволяет построить параллелограмм скоростей в любой точке потока внутри рабочего колеса центробежного насоса.

Коэффициент стеснения равен отношению действительной площади сечения потока к площади сечения, свободной от лопастей:

,

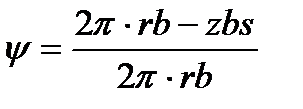или ,

где z – число лопастей;

s – толщина лопастей в рассматриваемом цилиндрическом сечении.

Обозначая через шаг – расстояние по окружности между одноименными точками смежных лопастей, получим, что коэффициент стеснения равен: ,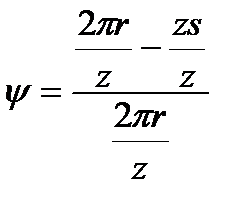

Или .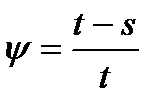

Толщина лопасти 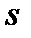может быть выражена через нормальную толщину 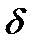и угол : .

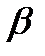Параллелограмм скоростей потока при входе в рабочее колесо может быть получен аналогичным образом. Коэффициент стеснения потока на входе в рабочее колесо в этом случае может быть принят равным от 0,75 для малых насосов до 0,83 для больших насосов.

План скоростей для выходного сечения рабочего колеса строится так же, как и для произвольной внутренней точки. Коэффициент стеснения потока на выходе из рабочего колеса в этом случае может быть принят равным от 0,90 для малых насосов до 0,95 для больших насосов.

Таким образом, зная:

- размеры рабочего колеса;

- форму лопастей;

- значение расхода;

- значение частоты вращения колеса насоса

можно определить:

- треугольники скоростей для входного, выходного и любого промежуточного сечений рабочего колеса;

- найти векторы абсолютной скорости;

- построить траектории абсолютного движения жидкости.

Характер движения жидкости до рабочего колеса насоса определяется конструкцией подводящего (всасывающего) водовода. Для обеспечения большей устойчивости потока в подводящем канале скорости течения назначаются постепенно нарастающими от входного патрубка к входу в колесо.

Диаметр входного патрубка определяется по сечению трубопровода, который в свою очередь рассчитывается исходя из допустимых потерь напора. Выравнивание поля скоростей по сечению потока непосредственно перед входом в рабочее колесо достигается с помощью конфузора, повышающего скорости на 15 – 20 %. Простейшей конструктивной формой является прямоосный конический патрубок. Однако такое решение возможно только при консольном расположении рабочего колеса насоса.

Отводящие каналы центробежных насосов должны обеспечивать:

- осесимметричность потока жидкости при выходе из рабочего колеса;

- преобразование кинетической энергии потока, выходящего из колесав энергию давления.

Наиболее характерной конструкцией отводящего канала одноступенчатых центробежных насосов является спиральный отвод, состоящий из:

- спирального канала;

- диффузора.

Спиральный канал собирает перекачиваемую жидкость, выходящую из рабочего колеса, и подводит ее к диффузору. При этом обеспечивается осевая симметрия потока за рабочим колесом насоса.

В диффузоре происходит снижение скорости потока и преобразование кинетической энергии жидкости в потенциальную энергию давления.

Поперечное сечение спирального отвода может иметь различную форму. Обычно оно бывает круглым.

Дата добавления: 2014-12-27