Политропные процессы

К политропным относятся термодинамические процессы, подчиняющиеся уравнению:

p·υⁿ = const, (2.48)

где n = (с – c_p)/(c _– c_v) – показатель политропы. Для конкретного политропного процесса величина n постоянна, но в различных политропных процессах показатель политропы может быть различным (в пределах ± ∞).

2.10.1 Соотношения политропного процесса. По аналогии с адиабатным процессом из уравнения (2.48) можно получить соотношения между параметрами политропного процесса:

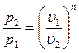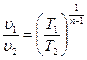; ; . (2.49)

Также по аналогии с адиабатным процессом работа политропного процесса равна:

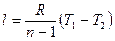, (2.50)

или с учетом уравнения состояния идеального газа:

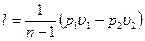, (2.51)

Подведенная теплота и изменение внутренней энергии в политропном процессе определяются уравнениями:

q = c (T ₂ – T ₁), (2.52)

Δ u = c _υ (T ₂ – T ₁). (2.53)

Политропный процесс является обобщающим по отношению к основным термодинамическим процессам. Из уравнения (2.48) могут быть получены уравнения для различных термодинамических процессов: изотермического (n = 1), изобарного (n = 0), адиабатного (n = k) и изохорного (n = ± ∞).

2.10.2 Теплоемкость политропного процесса. Подставляя значения l, q и Δ u из (2.50), (2.52) и (2.53) в уравнение первого закона термодинамики, получим:

,

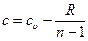или:

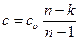. (2.54)

Видно, что теплоемкость в политропном процессе имеет вполне определенную величину, зависящую от значений с _υ, k и n. Причем в зависимости от показателя политропы, теплоемкость может быть положительной или отрицательной, а в отдельных случаях равна нулю (в адиабатном процессе) или бесконечности (в изотермическом процессе).

2.10.3 Политропные процессы в р – υ диаграмме. Если на диаграмме р – υ выбрать некоторую точку О и провести из нее основные термодинамические процессы как в сторону расширения (dυ > 0), так и в сторону сжатия (dυ < 0), то диаграмма разделится на несколько областей. В каждой области расположены процессы, объединенные общностью определенных свойств (рис. 2.11).

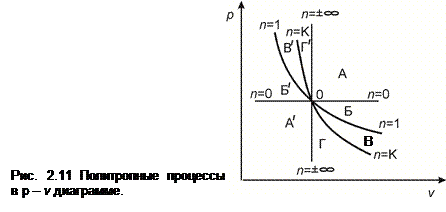1. В областях А и А ^’ располагаются политропные процессы, исходящие из точки О, у которых 0 > n > - ∞, в областях Б и Б ´: 1 > n > 0, в областях В и В ^´: k > n >1 и в областях Г и Г ^´: ∞ > n > k.

2. Все процессы, исходящие из точки О и расположенные правее изохоры (в областях А, Б, В, Г), совершают положительную работу (здесь dυ > 0) а расположенные левее изохоры (области А ^´, Б ^´, В ^´, Г ^´) – отрицательную (здесь dυ <0).

3. Все процессы, исходящие из точки О и расположенные выше изотермы (области В ^’, Г ^' А, Б), протекают с ростом температуры, а, следовательно, с ростом внутренней энергии, а процессы, расположенные ниже изотермы (области В, Г, А’, Б’) – с понижением Т и u. Это обусловлено тем, что, состояние газа в точках диаграммы р - υ, лежащих выше изотермы, исходящей из точки О, соответствует условию Т > Т ₀.

4. Все процессы, выходящие из точки О и расположенные выше адиабаты (области Г ^´, А, Б, В), протекают с подводом теплоты, а расположенные ниже адиабаты (области Г, А ´, Б ´, В ´) – с отводом теплоты. Например, изотермическое расширение газа идет с подводом теплоты, причем изотерма расширения расположена выше адиабаты.

Дата добавления: 2014-12-27