Обобщенное уравнение Бернулли

Вычтем из уравнения сохранения энергии (4.10) уравнение первого закона термодинамики для потока газа в форме (4.5), учитывая, что dq_r = dl_r. Тогда получим:

. (4.36)

Уравнение (4.36) называется обобщенным уравнением Бернулли. Интегрируя (4.36) от начального сечения 1 до конечного сечения 2 (рис. 4.2), получим интегральную форму этого уравнения:

. (4.37)

Интеграл в правой части уравнения (4.37) называют располагаемой работой, а величину υ·dр – элементарной располагаемой работой. Располагаемая работа на р - υ диаграмме (рис. 4.6) эквивалентна площади между осью ординат и кривой процесса (площадь 1-2-b-a). Она представляет собой разность работы расширения потока и работы проталкивания p₁v₁ – p₂v_2.

Обобщенное уравнение Бернулли можно интерпретировать, как баланс механических форм энергии в газовом потоке. Теплота не входит в это уравнение в явном виде, но она оказывает влияние на перераспределение энергии между отдельными ее слагаемыми. Все величины в уравнениях (4.36) и (4.37) отнесены к 1 кг газа (Дж/кг).

Для компрессора l _вн = - l _к, поэтому можно записать:

. (4.38)

Следовательно, внешняя работа, подводимая в компрессоре к газу, идет на располагаемую работу, изменение кинетической энергии потока и на работу по преодолению сил трения.

В случае турбины: l _вн. = l_r, поэтому:

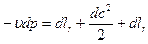(4.39)

Следовательно, в турбине (dр < 0) располагаемая работа расходуется на совершение внешней работы (работы на валу турбины), увеличение кинетической энергии газа и преодоление гидравлических потерь.

При течении газа в каналах (воздухо- и газопроводы) l _вн. = 0 и в этом случае:

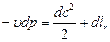. (4.40)

Если течение происходит без трения, то:

− υ·dр = с·dс. (4.41)

Из последнего выражения следует, что в таком потоке разгон газа (dс > 0) возможен лишь при понижении его давления (dр < 0), а торможение (dс < 0) сопровождается ростом давления (dр > 0). Наличие трения, естественно, сказывается количественно на параметрах потока. Например, при заданном уровне понижения давления наличие трения (l_r > 0) снизит прирост скорости потока (4.40) и, наоборот, в случае торможения потока при заданном уровне понижения скорости при наличии трения давление будет возрастать в меньшей степени, чем без трения.

Величина располагаемой работы может быть вычислена, когда известно уравнение процесса. Если процесс политропный, подчиняющийся уравнению (2.48), то, подставляя значение υ из этого уравнения в интеграл (1, 2 – начало и конец термодинамического процесса), после несложных преобразований можно найти:

, или .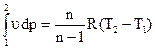

Полученные выражения называют политропной работой газового потока.

Дата добавления: 2014-12-27