Уравнение сохранения энергии в параметрах заторможенного потока. Частные случаи уравнения

КРИТИЧЕСКИЕ ПАРАМЕТРЫ ПОТОКА

Поскольку в идеальном газе k·R·T = a², то после преобразований получим:

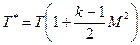. (4.17)

Подставляя значение Т ^* из (4.17) в (4.15), далее получим:

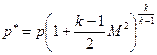. (4.18)

Если в каком-либо сечении потока газа число М = 1, т.е., скорость газа равна местной скорости звука, то параметры потока в этом сечении называются критическими. Найдем связь между критическими и полными параметрами потока. Так как М _кр. = 1, то из (4.17) и (4.18) следует:

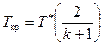, (4.19)

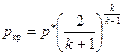, (4.20)

а из уравнения состояния идеального газа с учетом (4.19) и (4.20) имеем:

. (4.21)

По определению критическая скорость равна , или с учетом (4.19):

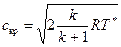. (4.22)

Таким образом, критические параметры потока для данного газа полностью определяются соответствующими полными (заторможенными) параметрами.

Запишем уравнение сохранения энергии (4.9) в параметрах заторможенного потока:

q _вн. − l _вн. = i ₂^* − i ₁^*. (4.23)

В случае идеального газа этому уравнению можно придать следующий вид:

q _вн. − l _вн. = с_р (Т ₂^* − Т ₁^*), (4.24)

или в дифференциальной форме:

dq _вн. − dl _вн. = с _р dТ ^*. (4.24*)

Рассмотрим частные случаи уравнения сохранения энергии.

4.6.1 Энергоизолированный поток. Поскольку в энергоизолированном потоке q _вн. = 0 и l _вн. = 0, то из (4.9) следует:

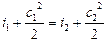, (4.25)

или

i ₁^* − i ₂^*. (4.25*)

Таким образом, в энергоизолированном потоке полная энтальпия (сумма энтальпии и кинетической энергии) постоянна. В случае идеального газа из (4.24) следует Т ₁^*= Т ₂^*. Следовательно, в энергоизолированном потоке идеального газа полная температура потока постоянна.

4.6.2 Компрессор. Обозначим через l _к работу, сообщаемую 1 кг газа в компрессоре (рис.4.4). Поскольку в компрессоре внешняя работа подводится к газу, то l _вн. = − l _к. Теплообменом между газом и элементами компрессора можно пренебречь (q _вн. = 0).

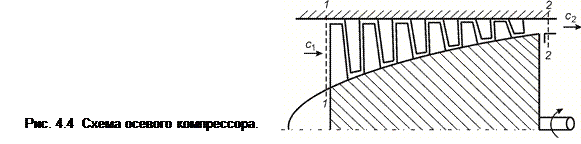Поэтому для газового потока в компрессоре из (4.9) следует

_, (4.26)

или:

l _к = i ₂^* − i ₁^*, (4.27)

т.е. внешняя работа в компрессоре идет на повышение полной энтальпии газа. В случае идеального газа:

l _к = с_р (Т ₂^* − Т ₁^*). (4.28)

Последнее выражение может быть использовано для экспериментального определения величины l _к по измеренным значениям Т ^*₁ и Т ^*₂. Зная работу l _к, можно найти мощность N _к, необходимую для вращения компрессора N _к, = G l _к, где G – расход газа через компрессор.

Рассмотрим идеальный компрессор. В идеальном компрессоре сжатие газа происходит без трения и теплообмена, т.е. является адиабатным. Вследствие этого, эффективную работу идеального компрессора называют адиабатной:

l _{ад к} = с_р (Т ₂^*_ад − Т ₁^*),

где Т ₂^*_ад. - температура газа на выходе из компрессора при адиабатных условиях сжатия. Вынося за скобки температуру Т ₁^* и учтя, что в адиабатном процессе

,

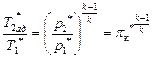получим:

. (4.29)

Здесь: − степень повышения полного давления в компрессоре.

4.6.3 Турбина. Поскольку в турбине (рис. 4.5) газ совершает работу, то l _вн. = l _т, где l _т – работа на валу турбины, отнесенная к 1 кг газа. Приняв q _вн. ≈ 0, из (4.9) для потока в турбине получим:

l _т , (4.30)

или

l _т = i ₁^* − i ₂^*. (4.31)

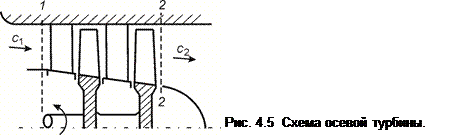
Следовательно, работа на валу турбины получается за счет уменьшения полной энтальпии газового потока. В случае идеального газа:

l _т = с_р (Т ₁^* – Т ₂^*). (4.32)

Зная величину l _т, и расход газа G, можно найти мощность, развиваемую турбиной, из уравнения N _т = G l _т.

Рассмотрим идеальную турбину, в которой отсутствуют теплообмен и трение и поэтому процесс расширения газа является адиабатным. Адиабатная работа турбины равна l _ад.т. = с_р (Т ₁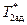^* − ), где 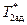- температура газа на выходе из турбины при адиабатном процессе расширения. Проведя преобразования, которые были сделаны выше, получим:

, (4.33)

где ‒ степень понижения полного давления газа в турбине.

4.6.4 Теплообменник. Камера сгорания. В теплообменнике внешняя энергия подводится (или отводится) только в виде теплоты q _вн.; поэтому из (4.23) следует:

q _вн. = i ₂^* − i ₁^*, (4.34)

а в случае идеального газа:

q _вн. = с_р (Т ₂^* − Т ₁^*). (4.35)

Соотношения (4.34) и (4.35) соблюдаются и для камеры сгорания; в этом случае под внешней теплотой q _вн. понимают количество теплоты, выделившееся в камере сгорания в результате процесса сжигания 1 кг газа.

Дата добавления: 2014-12-27