Потеря полезной работы в необратимых процессах

Рассмотрим изолированную термодинамическую систему, включающую теплоотдатчик с температурой Т ₁, теплоприемник с температурой Т ₂ и рабочее тело, посредством которого совершается работа. Изолированная система может производить работу, только находясь в неравновесном состоянии. В данном случае неравновесность определяется различием температур теплоотдатчика и теплоприемника (Т ₁ > Т ₂). Когда температуры Т ₁ и Т ₂ сравняются, система потеряет способность производить работу.

Осуществляя с рабочим телом произвольный цикл, можно получить полезную работу. Примем, что при осуществлении одного цикла температура теплоприемника Т ₂ не изменяется. Тогда в соответствии с (3.33)

Q ₂ = T ₂ ·Δ S ₂ , (3.34)

где Δ S ₂ – изменение энтропии теплоприемника при подводе к нему теплоты Q ₂.

Подставим (3.34) в уравнение (3.2) и получим:

L _ц = Q ₁ − T ₂ Δ S ₂. (3.35)

Уравнение (3.35) справедливо как для обратимого, так и для необратимого циклов. Если в рассматриваемой термодинамической системе превращение теплоты в работу производится посредством обратимого цикла Карно, то получается максимально возможное значение работы цикла. При этом энтропия изолированной системы не изменяется. Это позволяет записать для изолированной системы:

Δ S ₂ + Δ S ₁ = 0 и Δ S ₂ = − Δ S ₁. (3.36)

Здесь Δ S ₁ – изменение энтропии теплоотдатчика за цикл. Заметим, что энтропия рабочего тела после совершения цикла не изменится, так как рабочее тело возвращается в исходное состояние. С учетом (3.35) и (3.36) запишем выражение для максимальной полезной работы цикла:

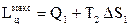. (3.37)

При осуществлении в системе необратимого цикла получаемая полезная работа (3.35) всегда меньше максимальной (3.37) на величину:

Δ L = L _ц^макс− L _ц = Т ₂ (Δ S ₁ + Δ S ₂) = Т ₂ Δ S _сист., (3.38)

где Δ S _сист – изменение энтропии рассматриваемой изолированной системы вследствие протекания в ней необратимых процессов. Здесь Δ S ₁ – величина отрицательная (уравнение3.32).

Потеря работоспособности системы Δ L тем выше, чем больше возрастание ее энтропии вследствие необратимости протекающих в ней процессов, т.е. вследствие диссипации энергии. Таким образом, возрастание энтропии изолированной системы может служить мерой диссипации энергии, т.е. мерой потери полезной работы.

3.9 КООРДИНАТЫ Т - s

Каждому состоянию любого вещества соответствует определенное значение энтропии s и температуры Т. Если использовать систему координат, где на оси ординат нанесены значения температуры Т, а на оси абсцисс – энтропии s, то в этих координатах равновесное состояние вещества изображается в виде точки, произвольный обратимый процесс изображается некоторой линией, а цикл – замкнутой совокупностью линий.

На рис. 3.6 изображен произвольный процесс 1 - 2 в Т - s координатах. Площадь заштрихованной площадки, соответствующая элементарному изменению энтропии ds при некоторой температуре Т равна, как следует из (3.16), элементарному количеству теплоты, участвующей в процессе dq = T·ds.

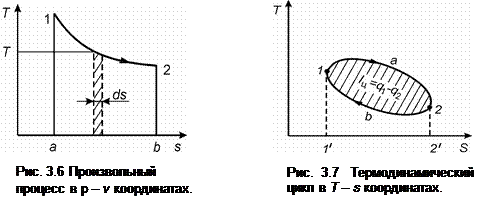
Вся теплота в процессе 1 - 2 определяется по формуле:

(3.39)

и изображается в Т - s координатах площадью а-1-2-b, ограниченной линией процесса, ординатами точек начала 1 – а и конца 2 – b процесса и осью абсцисс, если началом отсчета температуры на оси ординат является Т = 0. Если в процессе осуществляется подвод теплоты, то энтропия растет (s ₂ > s ₁) и состояние вещества изменяется в направлении от точки 1 к точке 2. При отводе теплоты ситуация обратная.

Рассмотрим цикл 1-а-2-b-1 в Т - s – координатах (рис. 3.7). В процессе 1-а-2 теплота q ₁ подводится к рабочему телу в количестве, эквивалентном площади 1’-1-а-2-2’-1’. В процессе 2-b-1 от рабочего тела отводится теплота q ₂ в количестве, равном площади 2’-2-b-1-1’-2’. Очевидно, что площадь, ограниченная циклом 1-а-2-b-1, равна q ₁ - q ₂ = l _ц, т.е. работе цикла. Термический к.п.д. цикла, изображенного в Т – s координатах, легко определяется как отношение площадей, соответствующих l _ц и q ₁ :

Ниже рассмотрены основные термодинамические процессы в Т - s координатах (рис.3.8).

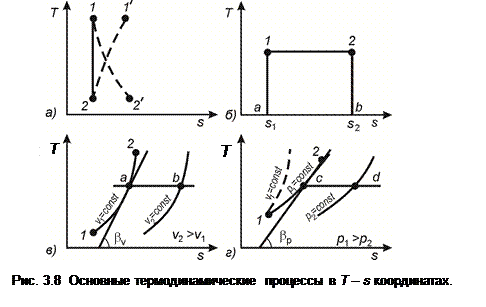3.9.1 Адиабатный процесс (рис. 3.8а). В этом случае dq = 0 и, следовательно:

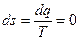. (3.40)

Интегрируя (3.40), получим s ₁ = s ₂ = const. Обратимому адиабатному процессу в Т - s координатах соответствует вертикальная линия 1 - 2. При адиабатном расширении температура газа падает (процесс 1 - 2), а при адиабатном сжатии – растет (процесс 2 -1). Вследствие постоянства энтропии в обратимом адиабатном процессе его называют также изоэнтропным. В дальнейшем все изоэнтропные процессы будем именовать адиабатными.

В необратимом адиабатном процессе, например, при наличии трения, энтропия растет. Причем возрастание энтропии происходит как при сжатии газа (процесс 2 – 1’, рис. 3.8а), так и при расширении (процесс 1 – 2 ’). Площадь под кривой процесса в Т - s координатах изображает в этом случае теплоту трения.

3.9.2 Изотермический процесс Т = const (рис. 3.8б) в Т - s координатах изображается горизонтальной линией 1 - 2. Теплота процесса эквивалентна площади прямоугольника а-1-2-b и равна:

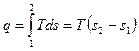. (3.41)

При подводе теплоты энтропия растет и процесс протекает от точки 1 к 2. При отводе теплоты – ситуация обратная. Изменение энтропии в изотермическом процессе может быть определено по уравнениям (3.25) или (3.27):

.

3.9.3 Изохорный процесс υ = const (рис. 3.8в) изображается в Т - s координатах логарифмической кривой 1-2. В соответствии с (3.25) изменение энтропии в обратимом изохорном процессе равно:

.

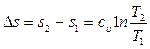Рассмотрим особенности протекания изохоры в Т - s координатах. Тангенс угла наклона касательной к изохоре υ = const определяется из уравнения (3.22)

.

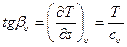С ростом температуры газа угол наклона касательной к оси абсцисс возрастает. Следовательно, изохора представляет собой кривую, обращенную выпуклостью к оси абсцисс. Изохоры, соответствующие различным значениям υ, эквидистантны между собой, т.к. при одинаковых температурах они имеют один и тот же угол наклона касательных. При изменении объема от υ ₁ до υ ₂ изохора смещается на отрезок a-b (рис.3.8в), величина которого определяется из уравнения (3.25) при условии постоянства температуры Т:

.

Изохора, соответствующая более высокому значению υ, располагается на большем удалении от оси ординат.

3.9.4 Изобарный процесс р = const (рис. 3.8г), как и изохорный, в Т - s координатах изображается логарифмической кривой. Изменение энтропии в обратимом изобарном процессе в соответствии с (3.27) равно:

.

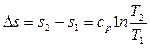Изобара является более пологой кривой, чем изохора. Это видно из сравнения углов наклона касательных к изохоре и изобаре (рис. 3.8 г). Для изобары dq = с _р dТ и поэтому:

,

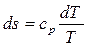откуда:

.

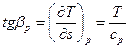Так как c _p > c _υ, то при одинаковых значениях Т имеем tgβ _p < tgβ _υ. Кривые изобарных процессов при различных значениях р, так же, как и изохоры, эквидистантны между собой. Расстояние между изобарами, соответствующими давлениям р ₁ и р ₂ (рис. 3.8 г), определяется по аналогии с изохорами из (3.27):

.

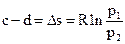В отличие от изохорных процессов с ростом давления изобары смещаются ближе к оси ординат.

3.9.5 Политропные процессы (рис. 3.9). В общем случае политропа в Т - s координатах изображается кривой линией, вид и положение которой зависят от показателя n. На рис.3.9 в Т - s координатах показаны типичные группы политроп в области расширения газа, свойства которых рассмотрены в п. 2.10.

В Т - s координатах можно построить диаграмму состояния как отдельного газа, так и смеси газов (например, воздуха). Пример общего вида части такой диаграммы приведен на рис. 3.10. Она состоит из сетки изохор и сетки изобар. На каждой из этих линий отмечается соответствующее ей значение удельного объема или давления. Горизонтальные и вертикальные линии изображают постоянные температуры и энтропии, значения которых наносятся обычно в виде масштаба на осях ординат и абсцисс.

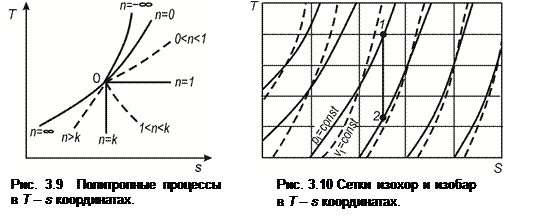С помощью Т - s диаграммы можно проводить исследования отдельных процессов и циклов, в которых данный газ используется как рабочее тело. Рассмотрим, например, адиабатное расширение газа. Если известны два параметра Т ₁ и р₁, характеризующие начальное состояние газа, то это позволяет нанести на диаграмму Т - s исходную точку 1, отвечающую этому состоянию (рис. 3.10). Через точку проводим вертикальную прямую (адиабату) до пересечения с линией, соответствующей заданному конечному параметру состояния газа, например, р ₂. Остальные конечные параметры легко определяются по изохоре и изотерме, которые проходят через точку 2. Использование Т - s диаграммы существенно упрощает расчеты, особенно при переменной теплоемкости газа.

3.10 КООРДИНАТЫ i - s

Недостатком диаграмм, построенных в Т - s координатах, является необходимость вычислять площади отдельных участков диаграммы при определении теплоты q и работы l процесса, изменения внутренней энергии Δ u и энтальпии Δ i газа. Этого недостатка лишены диаграммы состояния, построенные в координатах i - s (энтальпия – энтропия), где величины q, l, Δ u, Δ i определяются отрезками прямых. Данная особенность координат i, s упрощает анализ и расчет термодинамических процессов.

Рассмотрим протекание основных термодинамических процессов с идеальными газами в координатах i - s (рис. 3.11).

Обратимый адиабатный процессв координатах i - s, как и в координатах Т - s, изображается прямой вертикальной линией (s = const).

3.10.1 Изотермический процесс. Для идеального газа di = с_р dТ, поэтому:

.

Поскольку, в изотермическом процессе , то в случае идеального газа 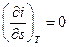. Следовательно, в i - s координатах изотерма идеального газа представляет собой горизонтальную прямую.

3.10.2 Изобарный процесс. В этом процессе dq = T·ds = c_p·dT = di. Изобара представляет собой кривую линию, тангенс угла наклона касательной которой равен:

.

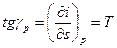Так как в изобарном процессе с ростом энтальпии температура газа Т увеличивается, то возрастает и угол γ_р. Следовательно, как и в T - s координатах, изобара обращена выпуклостью к оси абсцисс.

3.10.3 Изохорный процесс. По аналогии с изобарным процессом можно записать 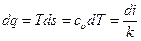, отсюда:

.

Следовательно, изохора так же, как и изобара, представляет собой кривую линию, обращенную выпуклостью к оси абсцисс. Взаимное расположение изобары и изохоры в i - s – координатах (рис. 3.11) аналогично их расположению в координатах T - s.

С помощью i - s диаграммы нетрудно определить основные термодинамические величины. Зная положение точек начала 1 и конца 2 процесса, непосредственно из диаграммы определяются параметры газа в этих точках р ₁, Т ₁, υ ₁, р ₂, Т ₂, υ ₂ и величины:

Δ i = i ₂ – i ₁ и Δ s = s ₂ – s _1.

Изменение внутренней энергии находится по формуле Δ u = Δ i – (p _2· υ ₂ – p ₁ υ ₁).

Величина теплоты и работы зависит от типа процесса и определяется следующим образом:

- в изобарном процессе q = Δ i, l = q − Δ u;

- в изохорном процессе q = Δ u;

- в изотермическом процессе q = T Δ s, l = q;

- в адиабатном процессе l = Δ u.

Особое значение i - s – диаграммы имеют в расчетах термодинамических процессов с реальными газами, у которых сильно меняются теплоемкость и другие свойства, что затрудняет использование аналитических формул.

Контрольные вопросы

1. Изложите содержание и приведите формулировки второго закона термодинамики.

2. Почему для анализа макроскопических процессов, которые сопровождаются тепловыми явлениями, в дополнение к первому закону необходим и второй закон термодинамики?

3. Может ли изолированная равновесная система производить полезную работу?

4. Изложите основные положения цикла Карно. Почему цикл Карно является эталоном для любого обратимого цикла, но не используется на практике?

5. Выполните анализ термического к.п.д. цикла Карно.

6. Сформулируйте второй закон термодинамики для равновесных и неравновесных процессов в математической форме.

7. Изложите физическое содержание энтропии.

8. Запишите изменение энтропии в обратимых термодинамических процессах.

9. Изобразите в Т- s диаграмме необратимые процессы расширения и сжатия.

10. Изобразите основные обратимые термодинамические процессы в i – s диаграмме.

РАЗДЕЛ 4

Дата добавления: 2014-12-27