И необратимых процессах

Из математики известно, что если интеграл по замкнутому контуру равен нулю, то подинтегральное выражение представляет собой полный дифференциал некоторой функции. Для подинтегральной функции из (3.12) введем следующее обозначение:

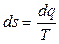. (3.16)

Тогда для обратимого кругового процесса можно записать:

. (3.17)

Функция s, полный дифференциал которой равен 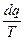(dq – теплота в обратимом процессе), называется энтропией.

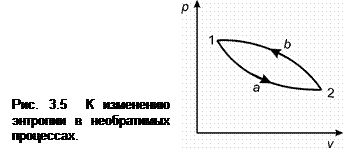
Очевидно, что величина интеграла 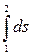, определенная для любого обратимого процесса перехода вещества из состояния 1 в состояние 2 (рис. 3.5), представляет собой изменение энтропии рабочего тела в рассматриваемом процессе. Изменение энтропии не зависит от пути процесса, а зависит только от параметров рабочего тела в начальном и конечном состоянии. Действительно:

,

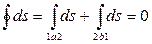но так как:

^,

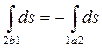то, следовательно:

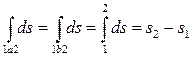(3.18)

Таким образом, энтропия является функцией состояния, величина которой однозначно определяется параметрами состояния. Отметим, что через s обозначается удельная энтропия, т.е. энтропия, отнесенная к 1 кг вещества 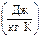; а энтропия, отнесенная к произвольному количеству вещества, обозначается через .

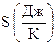Если в термодинамическую систему входит несколько тел, энтропии которых равны S ₁, S ₂, …, S _n, то энтропия системы в равна:

S _сист = S ₁+ S ₂ +… + S _n (3.19)

Из (3.16) следует, что энтропия отдельного тела или системы тел в обратимых термодинамических процессах может как возрастать, так и уменьшаться. Так как абсолютная температура Т всегда положительна, то подводу теплоты к телу или системе тел (dq > 0) соответствует возрастание энтропии (ds > 0), а отводу теплоты (dq <0) - уменьшение энтропии (ds < 0).

Определим величину энтропии какого-либо вещества путем интегрирования выражения (3.16):

^, (3.20)

где s ₀ – постоянная интегрирования.

В термодинамических расчетах определяется не абсолютное значение энтропии, а ее изменение Δ s в процессе, определяемое по уравнениям (3.18). Из (3.19) следует, что изменение энтропии термодинамической системы определяется как алгебраическая сумма изменений энтропии всех тел, входящих в систему. Тогда

Δ S _сист = Δ S ₁ + Δ S ₂ + … + Δ S _n. (3.21)

Выведем уравнения для определения изменения энтропии в процессах с идеальными газами. Подставив в (3.16) величину dq из (2.13), получим:

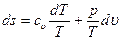. (3.22)

Поскольку для идеального газа

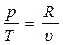, (3.23)

то:

. (3.24)

Интегрирование (3.24) при постоянной теплоемкости c_υ позволяет получить:

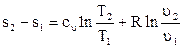. (3.25)

Из уравнения состояния для идеального газа следует:

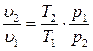(3.26)

Подставив (3.26) в (3.25), после простых преобразований получим:

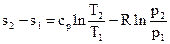. (3.27)

Уравнения (3.25) и (3.27) позволяют определить изменения энтропии в обратимом термодинамическом процессе идеального газа, если известны параметры состояния газа в исходной и конечной точках процесса.

Рассмотрим особенности изменения энтропии в необратимых процессах. Пусть рабочее тело переходит из состояния 1 (рис. 3.5) в состояние 2 произвольным необратимым процессом 1-а-2 и затем возвращается в исходное состояние обратимым процессом 2-b-1. Очевидно, что цикл 1-а-2-b-1 является необратимым и для него справедливо неравенство

, или .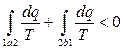

Интеграл 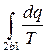, взятый по обратимому процессу 2-b-1, в соответствии с (3.18) равен разности энтропий s₁ – s₂. Тогда:

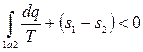, или

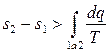(3.28)

Таким образом, в необратимых процессах изменение энтропии всегда больше интегральной суммы приведенных теплот данного процесса.

В дифференциальной форме уравнение (3.28) имеет вид:

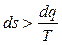. (3.29)

Соотношения (3.16) и (3.29) можно объединить в одно выражение:

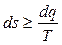, (3.30)

где знак равенства относится к обратимым процессам, а знак неравенства – к необратимым.

Выражение (3.30) рассматривается как аналитическая запись второго закона термодинамики.

Дата добавления: 2014-12-27