Уравнение сохранения энергии газового потока

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ ДВИЖУЩЕГОСЯ ГАЗА

В разделе 2 было показано, что уравнение первого закона термодинамики (п. 2.1) определяет баланс между теплотой, подведенной к телу (или отведенной от него), изменением внутренней энергии и работой расширения (сжатия), направленной на изменение объема. Для потока газа (жидкости) это уравнение можно интерпретировать как уравнение, выражающее закон сохранения и превращения энергии в системе координат, движущейся вместе с некоторым объемом, выделенным в потоке. При этом теплота, подводимая к газу, складывается из теплоты, подводимой от внешних источников q _вн., и теплоты, выделяемой в результате работы сил трения q _r. Поэтому уравнение первого закона термодинамики (2.3) для потока газа будет иметь следующий вид:

dq _вн + dq _r = du + p·dυ. (4.4)

Уравнение (4.4) применимо к любым газовым потокам, в том числе и нестационарным. Если в потоке не совершается работа изменения объема (p · dυ = 0), то вся теплота, подведенная к газу или отведенная от него, идет на изменение его внутренней энергии. Из сказанного следует, что, так же как и в неподвижной среде, тепловая форма энергии (внутренняя энергия; энергия, подводимая или отводимая в форме теплоты) может быть преобразована в механическую форму только при изменении объема газа.

В том случае, когда рабочее тело несжимаемо (dυ = 0), то подведенная теплота не может быть преобразована в какой-либо вид энергии механического движения (кинетическая энергия, потенциальная энергия и др.); рабочее тело только может только изменять внутреннюю энергию. Поэтому несжимаемая жидкость не может служить рабочим телом тепловых двигателей.

Уравнение первого закона термодинамики для потока газа (4.4) может быть также записано в следующем виде:

dq _вн + dq _r = di – υdp, (4.5)

которое вытекает из уравнения (2.23).

Уравнение сохранения энергии газового потока выводится на основе первого закона термодинамики, но в отличие от уравнения в форме (4.4) оно записывается в неподвижной системе координат.

Составим баланс энергии для массы газа, заключенной между сечениями 1 и 2 (рис.4.2), которая за некоторый небольшой промежуток времени переместилась в положение 1 ' – 2 '. На основании закона сохранения и превращения энергии внешняя энергия, подведенная к рассматриваемой массе газа извне, приведет к изменению ее внутренней энергии и, кинетической е _кин. и потенциальной е _пот. энергии.

Полное количество энергии, подведенное к газу, складывается из теплоты и работы внешних сил l _Σ, т.е.:

q − l _Σ = Δ и + Δ е _кин. + Δ е _пот.. (4.6)

Напомним, что согласно правилу знаков принятому в термодинамике работа, подведенная к телу, считается отрицательной, а работа, совершенная телом, – положительной.

Изменение любого вида энергии равно разности этого вида энергии в положениях 1 - 2 и 1 '– 2 '. Поскольку движение, установившееся в объеме 1 ' – 2 является общим для обоих положений, то изменение каждого вида энергии будет определяться разностью ее количеств в объемах 1 – 1 ' и 2 – 2 '. Нетрудно видеть, что масса газа в объемах 1 – 1 ' и 2 – 2 ' одинакова. Для упрощения выкладок примем, что она равна 1 кг. Будем считать, что перемещения Δх₁ и Δх₂ малы и, поэтому, параметры газа внутри каждого из этих объемов одинаковы. Тогда:

Δ и = и ₂ – и ₁ , , Δ е _пот. = g (H ₂ – H ₁). (4.7)

Работа l _Σ состоит из работы сил трения, работы проталкивания и внешней (эффективной) работы:

l _Σ = l _r + l _прот. + l _вн. (4.7*)

Работа сил трения полностью переходит в тепло трения, поэтому, l _r = q_r. Работа проталкивания производится внешними по отношению к выделенному объему силами давления: в сечении 1 – давлением р ₁, а в сечении 2 – р ₂. Силы давления, действующие на боковую поверхность потока, работы не производят, так как они нормальны к траекториям движения частиц газа. Сила давления в сечении 1 совершает работу над выделенным объемом газа (– р ₁ F ₁Δ x ₁) = − р _1· υ ₁, а в сечении 2 газ в рассматриваемом объеме совершает работу против силы р ₂ F ₂. Тогда: р ₂ F ₂ Δ x ₂ = р _2· υ ₂ и l _прот. = р ₂ υ ₂ − р ₁ υ ₁.

Внешняя (эффективная) работа – это работа, сообщаемая газу (или получаемая от него) внешними источниками или потребителями механической энергии (турбина, компрессор, насос и др.). Она является результатом воздействия гидродинамических сил газового потока на тела, перемещающиеся в этом потоке (например, лопатки турбины или компрессора). Подставляя (4.7) и (4.7*) в (4.6) и раскрывая величины q и l _прот, получим:

.

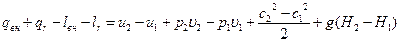Поскольку q _r = l _r, а энтальпия i = и + р·υ, то далее имеем:

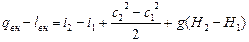. (4.8)

Уравнение (4.8) представляет собой уравнение сохранения энергии для газового потока, в котором все величины отнесены к 1 кг газа (Дж/кг). Это уравнение соблюдается для любых рабочих тел при стационарном движении, как при наличии трения, так и без него.

Для газовых потоков в элементах энергетических машин изменением потенциальной энергии можно пренебречь вследствие ее малости. Поэтому, в дальнейшем уравнение сохранения энергии будем использовать в следующем виде:

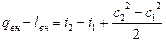, (4.9)

или в дифференциальной форме

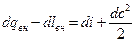. (4.10)

Уравнение сохранения энергии в форме (4.9) формулируется следующим образом: внешняя энергия, подведенная к потоку газа в форме теплоты и работы, расходуется на изменение энтальпии и кинетической энергии газа.

В случае идеального газа i ₂ – i ₁ = с_р· (Т ₂ – Т ₁), поэтому для идеального газа уравнение (4.9) можно также представить в виде:

, (4.11)

или в дифференциальной форме:

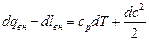. (4.12)

Дата добавления: 2014-12-27