Фазовые диаграммы

7.2.1 Фазовая p–t диаграмма. При рассмотрении отдельных фаз чистого вещества обычно имеют в виду его агрегатные состояния: твердое, жидкое и газообразное. Однако, в общем случае понятие «фаза» несколько шире понятия «агрегатное состояние», так как некоторые вещества в твердом состоянии, например, лед, углерод могут иметь несколько фаз.

Фазовый переход, т.е. переход вещества из одной фазы в другую, сопровождается изменением свойств вещества, выделением или поглощением теплоты (теплота фазового перехода). Равновесное сосуществование нескольких фаз возможно лишь при определенных сочетаниях параметров состояния (например, температуры и давления). Знание условий равновесного сосуществования различных фаз является важным для решения многих технических задач, например. для определения условий закипания жидкостей в гидравлических системах, оценки условий возникновения кавитации в насосах и др.

Анализ условий термодинамического равновесия фаз базируется на правиле фаз Гиббса. Оно устанавливает связь между числом независимых параметров состояния (степеней свободы системы) ψ, числом фаз k и числом компонентов системы n. Математически правило фаз Гиббса формулируется следующим образом:

ψ = n – k + 2.

Для чистого вещества (однокомпонентная система n = 1)правило фаз Гиббса имеет вид:

ψ = 3 – k.

В этом случае однофазная система (твердое тело, жидкость или газ) имеет две степени свободы, т.е. два независимых параметра состояния. Это означает, что если произвольно задать два параметра состояния (например, p и t), то все другие будут определены однозначно. Одновременно это означает, что в однофазном состоянии вещество может существовать при произвольных сочетаниях p и t.

Двухфазная система (k = 2) обладает только одной степенью свободы (ψ = 1); здесь произвольно может быть задан лишь один параметр состояния. Следовательно, равновесное сосуществование двух фаз (твердой и жидкой, жидкой и газообразной, твердой и газообразной) возможно лишь при определенном сочетании значений p и t; т.е. каждому значению p соответствует вполне определенная температура, при которой возможно сосуществование фаз.

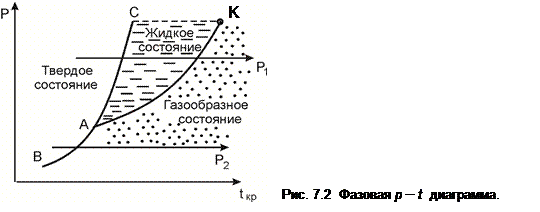На рис. 7.2 изображена типичная фазовая p – t диаграмма с линиями фазового равновесия. Здесь АК – линия фазового равновесия жидкости и газа (пара), АС – твердого тела и жидкости; АВ – линия твердого состояния и газа. Иными словами: АК – линия парообразования (конденсации), АС – линия плавления (затвердевания), АВ – линия сублимации (десублимации). Линию АК называют также линией насыщения, которая заканчивается критической точкой К. Три линии пересекаются в одной точке А, которая называется тройной точкой. В этой точке одновременно существуют три фазы, т.к. согласно правилу фаз Гиббса при k = 3 число степеней свободы однокомпонентной системы равно нулю (ψ = 0). Например, для воды в тройной точке p _А = 616 Па, t _А= 0,01°С, а для двуокиси углерода p _А = 0,518 МПа, t _А = – 56,7°С.

Пользуясь фазовой диаграммой, можно установить, в каком состоянии (твердом, жидком, газообразном, двух- или трехфазном) будет находиться конкретное вещество при заданных значениях p и t. Кроме того, с помощью фазовой диаграммы можно определить температуру фазового перехода при заданном давлении и наоборот.

Фазовая диаграмма устанавливает также характер перехода вещества из одного состояния в другое. Например, при p ₁ > p_А переход из твердого состояния в газообразное происходит через жидкое. При давлении p₂ < p_А существование вещества в жидком состоянии невозможно; здесь твердая фаза переходит в газообразную, минуя жидкую стадию. Вместе с тем при давлениях, превышающих давление в критической точке, невозможно сосуществование газообразной и жидкой фаз, а при температурах, превосходящих температуру в критической точке (см. далее), вещество существует лишь в газообразной (парообразной) фазе.

7.2.2 Фазовая p – v диаграмма. Процессы изменения параметров реального газа при фазовом переходе жидкость-пар наиболее наглядно можно представить с помощью p – v диаграммы (рис. 7.3).

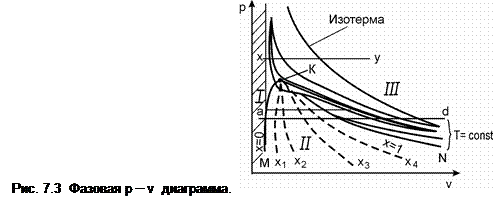
На данной диаграмме область равновесия двух фаз («жидкость – пар») изображается не линией, а занимает некоторую площадь. Здесь можно выделить три области: I – жидкое состояние, II – двухфазное состояние (фазовое равновесие «жидкость-пар») и III – газообразное (парообразное) состояние. Кривая МК – является геометрическим местом точек, определяющих состояние жидкости, нагретой до температуры кипения (насыщения) при соответствующем давлении. Она отделяет область жидкости от области насыщенных паров и называется пограничной кривой жидкости (здесь х = 0).

Точки кривой NК определяют состояние сухого насыщенного пара. Эта кривая отделяет область насыщенных паров от области перегретых паров и называется пограничной кривой пара; здесь х = 1,0. На p- vдиаграмме в области двухфазного состояния нанесены линии постоянной сухости пара (х ₁; х ₂ и т.д.). С ростом давления и, соответственно температуры, при которых происходит фазовый переход, удельный объем кипящей жидкости увеличивается, а удельный объем насыщенного пара уменьшается. При некотором, вполне определенном для каждого вещества давлении, пограничные кривые сходятся к точке К, которая называется критической точкой.

На рис. 7.3 нанесены несколько изотерм (Т = const). Видно, что в области перегретого состояния изотерма имеет вид, близкий к изотерме идеального газа. В области двухфазного состояния вещества («жидкость–пар») изотерма является одновременно и изобарой. Это непосредственно вытекает из правила фаз Гиббса, согласно которому двухфазная однокомпонентная система обладает только одной степенью свободы. В области жидкого состояния рост давления приводит к незначительному изменению объема жидкости из-за малой сжимаемости. При критической температуре горизонтальный участок превращается в точку (критическая точка), которая является точкой перегиба на этой изотерме. Состояние вещества в этой точке характеризуется критическими параметрами: давлением р _к, температурой Т _к и удельным объемом v _к. Критические параметры некоторых веществ приведены в табл.7.1.

Таблица 7.1 Критические параметры некоторых веществ

Вещество	t к, ºC	р к, МПа	Вещество	t к, ºC	р к, МПа
Гелий	-267,9	0,228	Аммиак	132,3	11,28
Водород	-239,9	1,294	Этиловый спирт
Азот	147,0	3,393	Вода	374,15	22,127
Кислород	-118,4	5,07	Углерод	~ 6000	~ 700
Двуокись кислорода	31,04	7,412	Ртуть		147,1

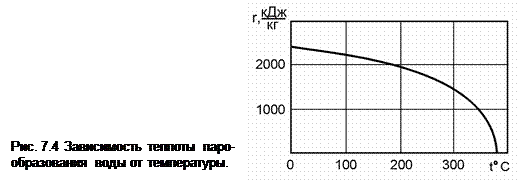
Критическая точка K принадлежит одновременно обеим пограничным кривым и соответствует состоянию вещества, при котором отсутствует разница между жидкостью и паром. Это иллюстрируется зависимостью теплоты парообразования от температуры для воды (рис. 7.4), из которой видно, что в критической точке теплота парообразования становится равной нулю (r = 0). При температуре выше критического значения изотермы не имеют горизонтальных участков. При этих температурах для любого давления вещество находится в парообразном (газообразном) состоянии, а вид изотерм по мере увеличения температуры приближается к изотермам идеального газа.

Из p – v диаграммы следует важный вывод о различном характере перехода жидкости в пар при различных давлениях. При докритических давлениях при подводе к жидкости теплоты последовательно происходят нагрев жидкости до температуры кипения, парообразование, во время которого вещество находится в двухфазном состоянии, и перегрев пара. При сверхкритических давлениях (линия x – y) переходиз жидкого состояния в газообразное происходитнепрерывно, минуя двухфазное состояние. Граница между жидкой и газообразной фазами в этом случае условна.

При переходе жидкости в пар при докритических давлениях осуществляется скачкообразное изменение свойств вещества. Как следует из рис. 7.5, где показана зависимость плотности водорода от температуры при двух давлениях, при сверхкритическом давлении этот процесс идет с непрерывным накапливанием различий между жидкостью и паром. Это следует иметь в виду при проектировании и анализе работы технических устройств, в которых возможны фазовые переходы (теплообменники, системы охлаждения, холодильные установки, парогенераторы силовых и энергетических установок).

.

Используя критические параметры вещества можно определить постоянные а и b в уравнении Ван-дер-Вальса: а = 27 R² T²_k/64 P_k, b = R T_k/8 P_k, R = 8 P_k v_k/3 T_k. Параметры вещества, отнесенные к соответствующим параметрам в критическом состоянии, называются приведенными параметрами:

.

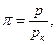
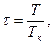
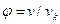Здесь р_к, Т_к – критические значения давления и температуры данного вещества. Используя приведенные параметры, уравнение Ван-дер-Вальса можно записать в следующем виде 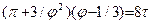, которое называется приведенным уравнением состояния Ван дер Вальса. Для всех веществ в критической точке приведенные параметры имеют одно и то же значение, равное единице.

Для практических расчетов с погрешностью 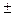15% можно использовать уравнение состояния реального газа в следующем виде:

p·υ = z∙R∙T, (7.2)

которое получено на основе закона соответственных состояний. Здесь z – коэффициент сжимаемости, зависящий от давления p и температуры T и определяемый экспериментально. На основе анализа опытных данных установлено, что с определенной точностью функция z = z (π, τ) является универсальной, т.е. достаточно общей для различных веществ. Для конкретного вещества она может быть определена из z -π диаграммы, приведенной на рис. 7.6.

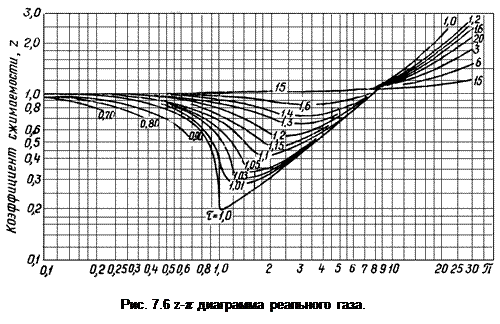
Отношение z_k = R·T_k / p_k· v _k в критической точке называется критическим коэффициентом и с учетом вышеприведенных соотношений для критических параметров (a, b, R) является постоянным и равным 8/3 =2,67.

Дата добавления: 2014-12-27