Перестановки. Размещения. Сочетания

Пусть есть некоторое конечное множество элементов U ={ a ₁, a ₂,..., a _n}. Рассмотрим набор элементов , где Î U, j = 1, 2,..., r.

Этот набор называется выборкой объема r из n элементов. Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).

Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным условиям, т.е. выбор производится по какому-нибудь принципу. Подсчет числа выборок основывается на двух правилах теории множеств.

Принцип суммы: если card A = m, card B = n и A Ç B = Æ, то card A È B = = m + n. На комбинаторном языке это означает: если объект A можно выбрать m способами, объект B другими n способами и их одновременный выбор невозможен, то выбор “ A или B ” может быть осуществлен m + n способами.

Принцип произведения: если card A = m, card B = n, то card (A ´ B)= m + n. На комбинаторном языке это означает: если объект A может быть выбран m способами, при любом выборе A объект B может быть выбран n способами, то выбор “ A и B ” может быть осуществлен m×n способами.

Пример 1. A = 10 {различных шоколадок}, B = 5 { различных пачек печенья}. Выбор “ A или B ” означает, что выбирается что-то одно и способов выбора в этом случае будет 15. Выбор “ A и B ” означает, что выбирается 1 шоколадка и 1 пачка печенья и различных вариантов для такого выбора будет 50.

Пример 2. Бросают 2 игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков?

Пусть m – число возможностей для выпадения четного числа на одной кости, n – число возможностей для выпадения нечетного числа. Здесь m = n = 3. По правилу произведения количество выпадения четных чисел, как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных и двух нечетных чисел будет 18.

Рассмотрим основные способы формирования выборок.

Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.

Из определения следует, что две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.

Перестановки. Упорядоченные выборки, объемом n из n элементов, где все элементы различны, называются перестановками из n элементов. Число перестановок из n элементов обозначается P_n.

Теорема. P = n!

Доказательство проводится по индукции. Очевидно, если n = 1, то перестановка только одна и P ₁ = 1!. Пусть для n = k теорема верна и P_k = k!, покажем, что она тогда верна и для n = k +1. Рассмотрим (k +1)- й элемент, будем считать его объектом A, который можно выбрать k +1 способами. Тогда объект B – упорядоченная выборка из оставшихся k элементов по k. B соответствии с индуктивным предположением объект B можно выбрать k! способами. По принципу произведения выбор A и B можно осуществить k!(k +1) = (k +1)! способами. Совместный выбор A и B есть упорядоченная выборка из k + 1 элементов по k + 1.

Пример 3. Сколько существует способов, чтобы расположить на полке 10 различных книг? Ответ: 10!

Можно рассуждать иначе. Выбираем первый элемент, это можно сделать n способами. Затем выбираем второй элемент, это можно сделать (n - 1) способами. По правилу произведения упорядоченный выбор двух элементов можно осуществить n ´(n - 1) способами. Затем выбираем третий элемент, для его выбора останется n - 2 возможности, последний элемент можно выбрать единственным способом. Мы вновь приходим к формуле: n (n - 1)(n - r)... 1.

Размещения. Упорядоченные выборки объемом m из n элементов (m < n), где все элементы различны, называются размещениями. Число размещений из n элементов по m обозначается .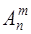

Теорема. =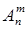

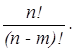
Обозначим x = 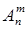. Тогда оставшиеся (n – m) элементов можно упорядочить (n – m)! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n – m)! способами, то совместный выбор “ A и B ” можно осуществить x ×(n – m)! способами, а выбор “ A и B ” есть перестановки и P_n = n! Отсюда x = =

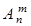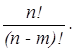
Рассуждая иначе: первый элемент выбираем n способами, второй – (n – 1) способами и т.д., m –й элемент выбираем (n – m + 1) способом. По принципу произведения вновь имеем: n (n – 1)...(n – m +1), что совпадает с .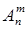

Пример 4. Группа из 15 человек выиграла 3 различных книги. Сколькими способами можно распределить эти книги среди группы?

Имеем = 15 ×14 ×13 = 2730.

Сочетания. Неупорядоченные выборки объемом m из n элементов (m < n) называются сочетаниями. Их число обозначается .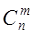

Теорема.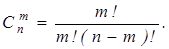

Доказательство. Очевидно, Действительно, объект A – неупорядоченная выборка из n элементов по m, их число 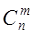. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.

Пример 5. Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?

Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.

Размещения с повторениями. Упорядоченные выборки объемом m из n элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается 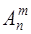(n).

Теорема. 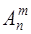(n) = n^m.

Доказательство. Первый элемент может быть выбран n способами, второй элемент также может быть выбран n способами и так далее, m -й элемент также может быть выбран n способами. По принципу произведения получаем n^m.

Пример 6. Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций?

Здесь n = 10, m = 4 и ответом будет 10⁴.

Пример 7. Рассмотрим вектор длины m, каждая координата которого может принимать всего 2 значения: 0 или 1. Сколько будет таких векторов?

Это есть выборка, объемом m из двух элементов.Ответ:2 ^m

Перестановки с повторениями. Пусть имеется n элементов, среди которых k ₁ элементов первого типа, k ₂ элементов второго типа и т.д., k_s элементов s -го типа, причем k ₁ + k ₂ +... + k_s = n. Упорядоченные выборки из таких n элементов по n называются перестановками с повторениями, их число обозначается C_n (k ₁, k ₂,..., k_s). Числа C_n (k ₁, k ₂,..., k _s) называются полиномиальными коэффициентами.

Теорема. C_n(k₁,..., k_s)=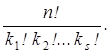

Доказательство проведем по индукции по s, т. е. по числу типов элементов. При s = 1 утверждение становится тривиальным: k ₁ = n, все элементы одного типа и C_n (n) = 1. В качестве базы индукции возьмем s = 2, n = k ₁ + k ₂. В этом случаем перестановки с повторениями превращаются в сочетания из n элементов по k ₁ (или k ₂): выбираем k ₁ место, куда помещаем элементы первого типа.

C_n (k ₁, k ₂) =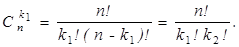

Пусть формула верна для s = m, т.е. n = k ₁ +... + k_m и

C_n(k ₁,..., k_m)=

Докажем, что она верна для s = m + 1 (n = k ₁ +... + k_m + k_{m +1}). В этом случае перестановку с повторениями можно рассматривать как совместный выбор двух объектов: объект A – выбор k _{m + 1} места для элементов (m + 1)-го типа; объект B – перестановка с повторениями из (n – k_{m +1}) элементов. Объект A можно выбрать способом, B – 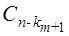(k ₁,..., k _m) способами. По принципу произведения

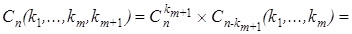
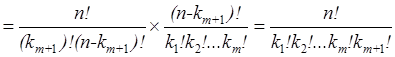
и мы получили требуемую формулу.

Замечание. Числа 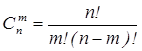называются биноминальными коэффициентами. Из этой формулы следует, что

Пример 8. Сколько различных слов можно получить, переставляя буквы в слове “математика”?

Решение. Буква “а” входит 3 раза (k ₁= 3), буква “м” – 2 раза (k ₂ = 2), “т” – 2 раза (k ₃ = 2), буквы “е”, ”к”, ”и” входят по одному разу, отсюда k ₃ = k ₄ = k ₅ = 1.

C ₁₀ (3, 2,, 2, 1, 1, 1) = 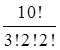=151200.

Сочетания с повторениями. Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m ´ n) называется сочетанием с повторением. Число сочетаний с повторениями обозначается (n).

Теорема. (n) = .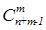

Доказательство. Пусть в выборку вошло m ₁ элементов первого типа, m ₂ элементов второго типа,... m _n – n -го типа. Причем каждое 0 £ m _i £ m и m ₁+ m ₂+...+ m_n = = m. Сопоставим этой выборке вектор следующего вида: Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { b_n } существует биекция (докажите это!). Следовательно, (n) равно числу векторов b_n. “ Длина вектора” b_n равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет .

Пример 9. В кондитерской имеется 7 видов пирожных. Покупатель берет 4 пирожных. Сколькими способами он может это сделать? (Предполагается, что пирожных каждого вида ³ 4).

Число способов будет

Пример10. Пусть V = { a, b, c }. Объем выборки m = 2. Перечислить перестановки, размещения, сочетания, размещения с повторениями, сочетания с повторениями.

1. Перестановки: { abc, bac, bca, acb, cab, cba }. P ₃=3!=6.

2. Размещения: {(ab), (bc), (ac), (ba), (cb), (ca)}.

3. Сочетания: {(ab), (ac), (bc)}.

4. Размещения с повторениями: {(ab), (bc), (ac), (ba), (cb), (ca), (aa), (bb), (cc)}. 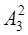(3)= 3² = 9.

5. Сочетания с повторениями: {(ab), (bc), (ca), (aa), (bb), (cc)}.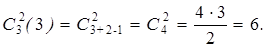

Дата добавления: 2014-12-27