Элементарные функции алгебры логики

ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ

Обозначения: E ₂={0,1}; Е 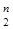= E ₂´ E ₂´...´ E ₂ – прямое произведение n сомножителей; (x ,.., x_n)Î E ₂, | E ₂| – мощность E ₂, | E ₂|=2, тогда | Е 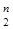|=2 ⁿ.

Определение 1. Функцией алгебры логики называется закон, осуществляющий отображение Е 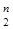E ₂, причем отображение всюду определено и функционально.

Так как множество Е 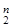конечно, то задать отображение Е 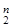Þ E ₂, означает задать множество наборов из Е 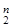и для каждого набора указать его образ в Е ₂.

Пример 1. Пусть n =2, тогда Е ={(0 0),(0 1),(1 0),(1 1)}, отображение Е Þ E ₂ задано, например, так: (0 0) Þ0; (0 1) Þ1; (1 0) Þ1; (1 1) Þ1.

Тем самым задана функция, для которой мы будем использовать стандартное обозначение f (x ₁, x ₂), записывая эту функцию в виде таблицы:

x 1	x 2	f (x 1, x 2)

Здесь x ₁ и x ₂ обозначают названия столбцов, а f – символ, обозначающий отображение. Следует обратить внимание, что функции f (x ₁, x ₂) и f (y ₁, y ₂) задают одно и то же отображение, и их таблицы отличаются только названиями столбцов.

Определение 2. Таблица, задающая функцию f (x ₁, x ₂,..., x_n), называется таблицей истинности для этой функции.

Рассмотрим функции одной переменной. Их будет всего 4, они задаются следующими таблицами истинности:

x	f 0(x)

функция называется константой 0, записывается f ₀(x) 0;

x	f 1(x)

функция называется тождественной, записывается f ₁(x)= x;

x	f 2(x)

функция называется «не x» и записывается f ₂ (x)= ;

x	f 3(x)

функция записывается f ₃(x) 1 и называется константой 1. Если стандартным расположением переменной x считать 0 в первой строке и 1 во второй, то функции f ₀, f ₁, f ₂, f ₃ определяются однозначно наборами значений: f ₀=(0,0), f ₁=(0,1), f ₂=(1,0) и f ₃=(1,1). Наборы значений функций составляют множество E ₂´ Е ₂, поэтому количество функций одной переменной равно | E ₂ E ₂|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.

Рассмотрим функции двух переменных f (x ₁, x ₂). Функции двух переменных определены на множестве Е ={(0 0),(0 1),(1 0),(1 1)}, эти наборы переменных из Е можно тоже рассматривать как двоичные коды чисел 0,1,2,3, именно такой порядок расположения наборов (x ₁, x ₂) будем считать стандартным. Тогда функции f (x ₁, x ₂) определяются однозначно наборами значений (b ₁, b ₂, b ₃, b ₄), где каждое b_i Î E ₂, поэтому (b ₁, b ₂, b ₃, b ₄)Î Е . Следовательно, число функций двух переменных равно 2⁴=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции.

x 1 x 2

f 0

f 1

f 2

f 3

f 4

f 5

f 6

f 7

f 8

f 9

f 10

f 11

f 12

f 13

f 14

f 15

0 0 0 1 1 0 1 1

Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их.

1) f ₁(x ₁, x ₂) = (x ₁& x ₂), читается «конъюнкция х ₁ и х ₂», иногда вместо знака & употребляют знак 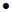или вообще его опускают, пишут (х ₁ х ₂). (х ₁& х ₂) совпадает с обычным произведением х ₁ х ₂ и совпадает с min(x ₁, x ₂). Эту операцию называют также логическим умножением.

2) f ₆(x ₁, x ₂) = (x ₁Å x ₂) – сложение х ₁ и х ₂ по модулю два, иногда пишут (х ₁+ х ₂) _{mod 2}.

3) f ₇(x ₁, x ₂) = (x ₁Ú x ₂), читается «х ₁ дизъюнкция х ₂», она совпадает с max(x ₁, x ₂), ее называют логическим сложением.

4) f ₈(x ₁, x ₂) = (x ₁ x ₂), читается «х ₁ стрелка Пирса х ₂» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.

5) f ₉(x ₁, x ₂) = (x ₁~ x ₂), читается «х ₁ эквивалентно х ₂».

6) f ₁₃(x ₁, x ₂) =(x ₁ 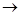x ₂), читается «х ₁ импликация х ₂», иногда обозначается (х₁Éх₂), т. е. х₁ влечет х₂.

7) f ₁₄(x ₁, x ₂) = (x ₁| x ₂), читается «х ₁ штрих Шеффера х ₂», она является отрицанием конъюнкции.

Cимволы ,&,Ú, 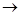,~, ,Å,|, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи», а 1 – «истине», а функции алгебры логики называются еще и блевыми функциями.

Рассмотрим функции f (x ₁... x_n), где (x ₁... x_n)Î Е 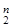, тогда число наборов (x ₁... x_n),где функция f (x ₁... x_n) должна быть задана, равно | Е 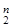|=2 ⁿ. Обозначим множество всех функций двузначной алгебры логики Р ₂. Обозначим через Р ₂(n) число функций, зависящих от n переменных. Очевидно, Р ₂(n)=2^{2 n}.

С ростом n число Р ₂(n) быстро растет: P ₂(1)=4, P ₂(2)=16, P ₂(3)=256, P ₂(4)=65536. При больших n табличный способ задания функций становится неприемлемым, используется формульное задание функций. Но прежде чем ввести понятие формулы, дадим определение существенной переменной.

Определение 3. Функция f (x ₁,..., x_{i –1}, x_i, x_{i +1},..., x_n) существенно зависит от х_i, если существуют такие значения a ₁,... a_{i –1}, a_{i +1},... a_n переменных x ₁,... x_{i –1}, x_{i +1},... x_n, что f (a ₁,... a_{i –1}, 0, a_{i +1}... a_n)¹ f (a₁... a_{i –1}, 1, a_{i +1}... a_n). Тогда переменная х_i называется существенной переменной. В противном случае х_i называется фиктивной переменной.

Дата добавления: 2014-12-27