
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Некоторые свойства элементарных функций
|
|
|
|
1. Идемпотентность & и Ú: х & x = x, x Ú x = x.
2. Коммутативность &,Ú,Å,|,~,  .
.
3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к Ú: x &(y Ú z)= xy Ú xz,
б) Ú по отношению к &: x Ú(y & z)=(x Ú y)&(x Ú z),
в) & по отношению к Å: x (y Å z)= xy Å xz.
5. Инволюция:  = х.
= х.
6. Правило де Моргана: 
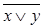 =
= 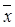 &
& 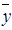 и
и 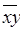 =
= 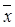 Ú
Ú 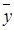 .
.
7. Законы действия с 0 и 1:
x Ú0= x, x Ú1=1, x Ú 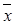 =1, x &0=0, x &1= x, x &
=1, x &0=0, x &1= x, x &  =0, x Å1=
=0, x Å1=  , x Å0= x.
, x Å0= x.
8. Самодистрибутивность импликации: x 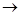 (y
(y 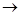 z)=(x
z)=(x 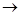 y)
y) 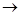 (x
(x 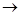 z).
z).
Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют.
Проверим для примера самодистрибутивность импликации: x 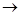 (y
(y 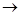 z)=(x
z)=(x 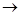 y)
y) 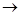 (x
(x 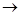 z).
z).
| x | y | z | y 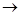 z z
| x 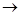 (y (y 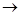 z) z)
| x 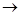 y y
| x 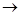 z z
| 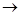
|
Следствия из свойств элементарных функций
1. Законы склеивания:
xy Ú x 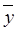 = x (y Ú
= x (y Ú  )= x
)= x 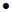 1= x (дистрибутивность & относительно Ú);
1= x (дистрибутивность & относительно Ú);
(x Ú y)&(x  )= x
)= x 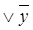 y = x Ú 0= x (дистрибутивность Ú относительно &).
y = x Ú 0= x (дистрибутивность Ú относительно &).
2. Законы поглощения:
x Ú xy = x (1Ú y)= x 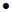 1= x; x &(x Ú y)= x Ú xy = x.
1= x; x &(x Ú y)= x Ú xy = x.
Свойства элементарных функций и теорема о замене подформул на эквивалентные позволяют упрощать формулы.
Пример 3:
Упростим формулы:
1. x 2 x 3Ú x 1 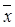 2 x 3 = x 3(x 2Ú x 1
2 x 3 = x 3(x 2Ú x 1  2) = x 3((x 2Ú x 1)&(x 2Ú
2) = x 3((x 2Ú x 1)&(x 2Ú 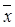 2)) = (x 1Ú x 2) x 3.
2)) = (x 1Ú x 2) x 3.
2. x 1Ú  1 x 2Ú
1 x 2Ú 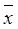 1
1 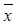 2 x 3Ú
2 x 3Ú 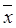 1
1  2 x 3 x 4 = x 1Ú
2 x 3 x 4 = x 1Ú 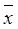 1(x 2Ú
1(x 2Ú 
 2
2 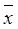 3 x 4) = x 1Ú
3 x 4) = x 1Ú 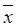 1(x 2Ú x 3Ú
1(x 2Ú x 3Ú 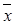 2
2 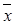 3 x 4) = (x 1Ú
3 x 4) = (x 1Ú 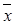 1)(x 1Ú x 2Ú x 3Ú
1)(x 1Ú x 2Ú x 3Ú 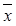 2
2 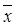 3 х 4) = x 1Ú(x 2Ú x 3)Ú(
3 х 4) = x 1Ú(x 2Ú x 3)Ú(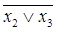 ) x 4 = x 1Ú(x 2Ú х 3Ú(
) x 4 = x 1Ú(x 2Ú х 3Ú( ))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
))(x 2Ú x 3Ú x 4) = x 1Ú x 2Ú x 3Ú x 4.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!