Полные системы

Полнота, примеры полных систем

Определение. Система функций { f ₁, f ₂,..., f _s,...}Ì P ₂ называется полной в Р ₂, если любая функция f (x ₁,..., x_n) Î P ₂ может быть записана в виде формулы через функции этой системы.

1. P ₂ – полная система.

2. Система M ={ x ₁& x ₂, x ₁Ú x ₂, } – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.

Пример 1. Неполные системы: { }, {0,1}.

Лемма (достаточное условие полноты)

Пусть система U = { f ₁, f ₂,..., f_s,...} полна в Р ₂. Пусть B = { g ₁, g ₂,..., g_k,...} – некоторая система из Р ₂, причем любая функция f_i Î U может быть выражена формулой над B, тогда система B полна в Р ₂.

Доказательство. Пусть h(x₁,..., x_n) Î P₂, т.к. U полна в Р₂, то h(x₁,..., x_n) = =N[f₁,..., f_s,...] = N[L₁[g₁,..., g_k],..., L_s[g₁,..., g_k],...] = U[g₁,..., g_k]. Здесь мы воспользовались тем, что для любого i 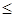n f_i может быть выражена формулой над B, поэтому f_i=L_i[g_i,..., g_k].

3. Система { x ₁Ú x ₂, } – полна в P ₂.

Возьмем в качестве полной в Р ₂ системы U ={ x ₁Ú x ₂, , x ₁& x ₂}, B ={ x ₁Ú x ₂, }. Надо показать, что x ₁& x ₂ представляется формулой над B. Действительно, по правилу Де Моргана получим: x ₁& x ₂= .

С помощью этой леммы докажем полноту еще ряда систем.

4. Система { x ₁& x ₂, } – полна в Р ₂.

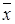5. Система { x ₁| x ₂} полна в Р ₂. Для доказательства возьмем в качестве полной в Р ₂ системы U = { x ₁& x ₂, } и выразим х ₁& х ₂ и через х ₁| x ₂ :

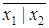= x ₁ | x ₁, x ₁ & x ₂ = = (x ₁| x ₂)|(x ₁| x ₂).

6. Система { x ₁ x ₂} полна в Р ₂. U = { x ₁Ú x ₂, }, = x ₁ x ₁, x ₁Ú x ₂ = = (x ₁ x ₂) (x ₁ x ₂).

7. Система { x ₁& x ₂, x ₁Å x ₂, 0, 1}, U = { x ₁& x ₂, }, = x ₁Å1.

Следствие. Полином Жегалкина.

f (x ₁,..., x_n) Î P ₂, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как { x ₁& x ₂, x ₁Å x ₂, 0, 1} полна в Р ₂. В силу свойства x & (y Å z) = xy Å xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х 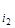х ... х , соединенных знаком Å. Такой полином называется полиномом Жегалкина.

Общий вид полинома Жегалкина:

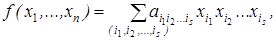
где 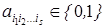, s = 0, 1,..., n, причем при s = 0 получаем свободный член а ₀.

Дата добавления: 2014-12-27