Функции k - значной логики

Теорема о достаточности четырех функций.

Из любой полной в Р ₂ системы функций можно выделить полную подсистему, состоящую не более чем из четырех функций.

Доказательство. Пусть { f ₀, f ₁, f_L, f_M, f_S } – полная система функций, тогда она не лежит целиком ни в одном из классов T ₀, T ₁, L, M, S. Следовательно, в системе есть функции f ₀Ï T ₀, f ₁Ï T ₁, f_L Ï L, f_S Ï S и f_m Ï M. Система { f ₀, f ₁, f_L, f_M, f_S } Í P ₂ и образует полную систему в Р ₂. Рассмотрим функцию f ₀: f ₀(0,..., 0) = 1.

Если f ₀(1,..., 1) = 0, то f ₀Ï T ₁ и f ₀Ï M, тогда { f ₀, f_S, f _L} – полная система из трех функций.

Если f ₀(1,..., 1) = 1, то f ₀Ï S и { f ₀, f ₁, f_L, f_M } образует полную систему из четырех функций.

Пример 1, приведенный выше, показывает, что цифру 4 в общем случае уменьшить нельзя, из полной системы { x ₁ x ₂,0,1, x ₁Å x ₂Å x ₃} нельзя выделить полную подсистему.

Следствие. Базис в Р ₂ может состоять максимум из четырех функций.

Введем обозначение: E_к ={0, 1, 2,..., k –1}.

Функция k -значной логики, зависящая от n переменных, – это закон, отображающий 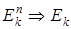. Множество функций k -значной логики обозначается как Р_k. Функция из Р_k полностью определена, если задана ее таблица истинности, т.е. заданы значения на всех наборах. Наборы можно рассматривать как записи в k -ичной системе счисления чисел от 0 до k –1, всего наборов kⁿ. Функций из Р_k, зависящих от n переменных, будет kⁿ. | P ₃(n)|, например, будет 3, если n = 2, то | P ₃(2)| = 3⁹ = 19683 (k =3, n =2).

x 1 x 2... xn -1 xn	f
0 0... 0 0 0 0... 0 1 ................... 0 0... 0 k –1 0 0... 1 0 ................... k –1 k –1... k –1 k –1	. . . . . . .

В k - значной логике также есть функции, которые называются элементарными. Приведем некоторые из них, примеры будем приводить для k = 3 и n = 2.

1. Циклический сдвиг или отрицание Поста: 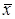= x +1(mod k).

2. Зеркальное отображение или отрицание Лукосевича: N_x = k –1– x.

Эти две функции являются обобщением отрицания.

3. J_i (x)={ k -1, x = i, I = 0, 1, 2,..., k –1}.

x 1	x 2	Nx	J 0(x)	J 1(x)	J 2(x)

4. min (x ₁, x ₂) – обобщение конъюнкции;

5. x ₁× x ₂(mod k) – второе обобщение конъюнкции;

6. max (x ₁, x ₂) – обобщение дизъюнкции;

7. x ₁+ x ₂(mod k) – сумма по mod k.

x 1	x 2	min (x 1, x 2)	x 1 x 2(mod 3)	max (x 1 x 2)	x 1+ x 2(mod 3)

Принято min (x ₁, x ₂) обозначать x ₁& x ₂, max (x ₁, x ₂) обозначать x ₁Ú x ₂.

Как и в двузначной логике, можно ввести понятие формулы над множеством и ставить вопрос о полной в Р_k системе функций.

Дата добавления: 2014-12-27