
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи и упражнения по функциям алгебры логики 2 страница
|
|
|
|
1) 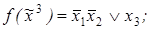
2) 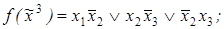
3) 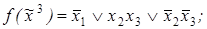
4) 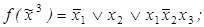
5) 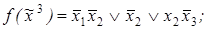
6) 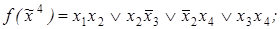
7) 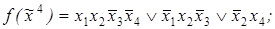
8) 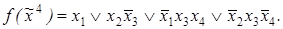
Ответы:
2) 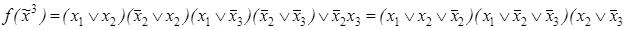

5) 
17. Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
1) 
2) 
3) 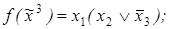
4) 
5) 
6) 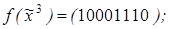
7) 
8) 
9) 
10) 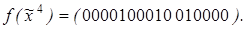
Ответы:
1) 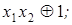
 3)
3) 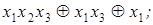 6)
6) 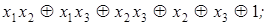
10) 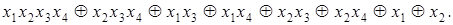
18. Методом треугольника Паскаля построить полином Жегалкина для этой функции, если:
1) 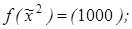 2)
2) 
3)  4)
4) 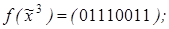
5)  6)
6) 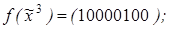
7) 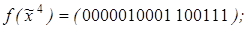 8)
8) 
9)  10)
10) 
Ответы:
1)  4)
4) 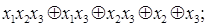 7)
7) 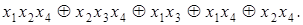
19. Представив функцию 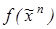 формулой над множеством связок {&,
формулой над множеством связок {&,  }, преобразуйте полученную формулу в полином Жегалкина функции
}, преобразуйте полученную формулу в полином Жегалкина функции 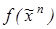 (используя эквивалентности
(используя эквивалентности 
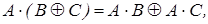
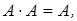
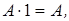

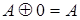 ):
):
1) 
2) 
3) 
4) 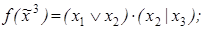
5) 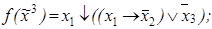
6) 
7) 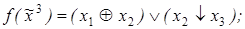
8) 
9) 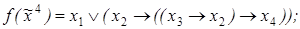
10) 
Ответы:
1) 
3) 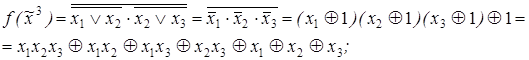
9) 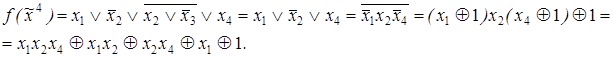
20. Построить множество всех функций, зависящих от переменных x 1, x 2 и принадлежащих замыканию множества А:
1) 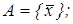
2) 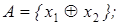
3) 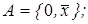
4) 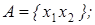
5) 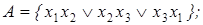
6) 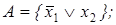
7) 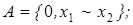
8) 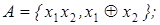
9) 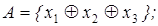
10) 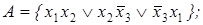
11) 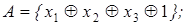
12) 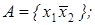
13) 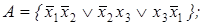
14) 
15) 
Ответы: 1)  2)
2)  3)
3) 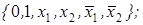
4)  5)
5)  6)
6) 
21. Покажите, что  , выразив
, выразив 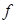 формулой над множеством А:
формулой над множеством А:
1) 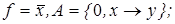
2) 
3) 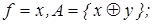
4) 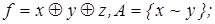
5) 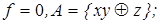
6) 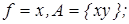
7) 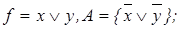
8) 
9) 
10) 
11) 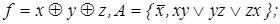
12) 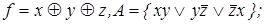
13) 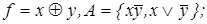
14) 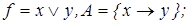
15) 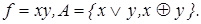
Ответы: 1) 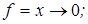 2)
2)  3)
3) 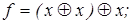 4)
4)  5)
5)  6)
6) 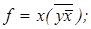 7)
7) 

22. Выписать все попарно неконгруэнтные функции 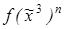 , принадлежащие замыканию множества А:
, принадлежащие замыканию множества А:
1)  2)
2) 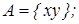 3)
3) 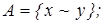 4)
4) 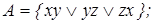
5) 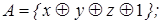 6)
6) 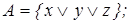 7)
7) 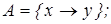 8)
8)  9)
9) 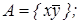 10)
10) 
Ответы: 1) 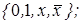 2)
2) 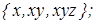 3)
3) 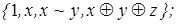 4)
4)  5)
5) 
23. Из полной для класса [ A ] системы выделить базис:
1)  2)
2)  3)
3)  4)
4) 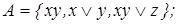
5)  6)
6) 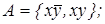
7) 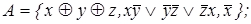 8)
8)  9)
9)  10)
10) 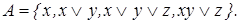
Ответы: 1) 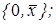 2)
2)  3)
3) 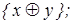 4)
4)  5)
5) 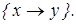
24. Сведением к заведомо полным системам в P 2 показать, что множество А является полной системой в P 2:
1) 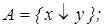
2) 
3) 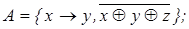
4) 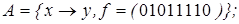
5) 
6) 
7) 
8) 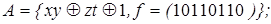
9) 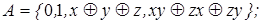
10) 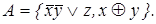
Ответы: 1)система  является полной в P 2, поскольку всякая
является полной в P 2, поскольку всякая 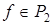 может быть представлена в виде ДНФ или КНФ. С другой стороны,
может быть представлена в виде ДНФ или КНФ. С другой стороны, 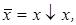
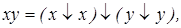
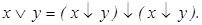
2) имеем 

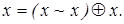 Система
Система  полна, поскольку
полна, поскольку 
3) имеем 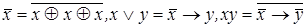 ;
;
4) имеем  ;
;
5) имеем 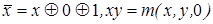 ;
;
25. Выяснить, является ли функция f самодвойственной:
1) 
3) 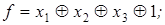
5) 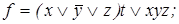
7) 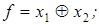
2) 
4) 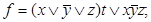
6) 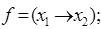
8) 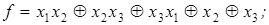
9) 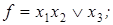
11) 
13) 
15) 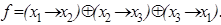
10) 
12) 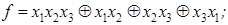 14)
14) 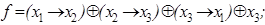
Ответы: 1),3),4),8),10) – является; 2),5),6),7),9) – не является.
26. Выяснить, является ли самодвойственной функция f, заданная векторно:
1) 
3) 
5) 
7) 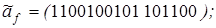
9) 
11) 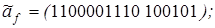
13) 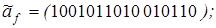
15) 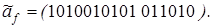
2) 
4) 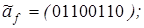
6) 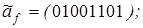
8) 
10) 
12) 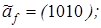
14) 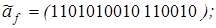
Ответы: 1),3),5),6),7),8) – является; 2),4),9),10) – не является.
27. Выяснить, является ли множество А самодвойственным:
1) 
2) 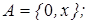
3) 
4) 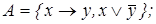
5) 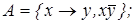
6) 
7) 
8) 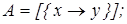
9) 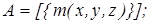
10) 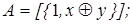
11) 
12) 
13) 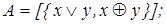
14) 
15) 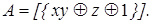
Ответы: 1),3),5-7),10) – является; 2),4),8),9) – не является.
28. Представив функцию f полиномом, выяснить, является ли она линейной:
1) 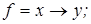
2) 
3) 
4) 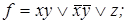
5) 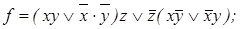
6) 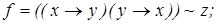
7) 
8) 
9) 
10) 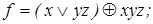
11) 
12) 
13) 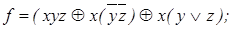
14) 
15) 
Ответы: 2),3),5),6),8),9)–является. 1),4),7),10)–не является.
29. Выяснить, является ли линейной функция f, заданная векторно:
1) 
2) 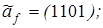
3) 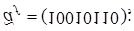
4) 
5) 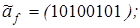
6) 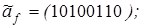
7) 
8) 
9) 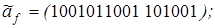
10) 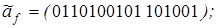
11) 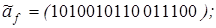
12) 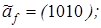
13) 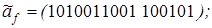
14) 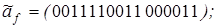
15) 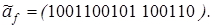
Ответы: 1),3),4),5),7),8),9),10) – является; 2),6) – не является.
30. Доказать, что система А полна в L. Выяснить, является ли система A базисом в L:
1) 
2) 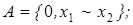
3) 
4) 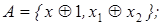
5) 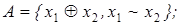
6) 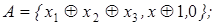
7) 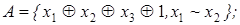
8) 
9) 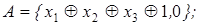
10) 
11) 
12) 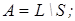
13) 
14) 
15) 
Ответы: 1)с помощью суперпозиции из функции 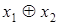 можно получить любую функцию вида
можно получить любую функцию вида  , путем подстановки 1-любую функцию вида
, путем подстановки 1-любую функцию вида 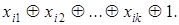 Система А является базисом;
Система А является базисом;
2),3),4),5),7),8),9) – является; 6),10) – не является.
31. Выяснить, принадлежит ли функция f множеству T 1\ T 0:
1) 
2) 
3) 
4) 
5) 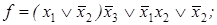
6) 
7) 
8) 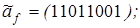
9) 
10) 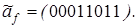
Ответы: 1),3),4),6),8),9) – является; 2),5),7),10) – не является.
32. Подсчитать число функций, зависящих от переменных x 1,…, xn и принадлежащих множеству А:
1) 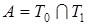 ;
;
2) 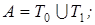
3) 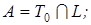
4) 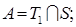
5) 
6) 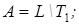
7) 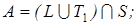
8) 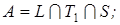
9) 
10) 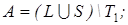
11) 
12) 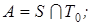
13) 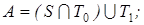
14) 
15) 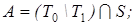
16) 
17) 
18) 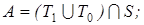
19) 
20) 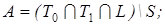
21) 
22) 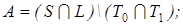
23) 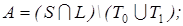
24) 
25) 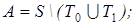
26) 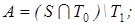
27) 
28) 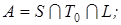
29) 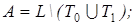
30) 
31) 
32) 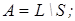
33) 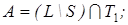
34) 
35) 
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1798; Нарушение авторских прав?; Мы поможем в написании вашей работы!