Теорема Жегалкина

Каждая функция из 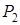может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

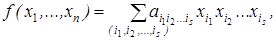
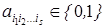, s = 0, 1,..., n. Доказательство. Любая функция из Р ₂ может быть представлена формулой над { x ₁ & x ₂, x ₁Å x ₂, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции f (x ₁,..., x_n) от n переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности, 2 ⁿ. Подсчитаем число различных полиномов Жегалкина от n переменных, т.е. число вариаций вида: 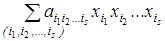. Число наборов 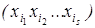равно числу всех подмножеств множества { x ₁,..., x_n }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2 ⁿ, а так как каждый набор входит с коэффициентом 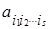, принимающим два значения: 0 или 1, то число всевозможных полиномов будет 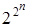. Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.

Определение. Функция f (x ₁,..., x_n), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а ₀ Å а ₁ х ₁ Å а ₂ х ₂ Å... Å а_nх_n, называется линейной.

Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Доказательство. Пусть f (x ₁,..., x_n) – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение x_ix_j. Будем считать для простоты, что x ₁ x ₂ в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде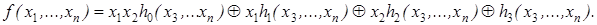

Функция h ₀ не есть тождественный нуль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением x ₁ x ₂. Тогда существует набор (a ₃, …, a_n) из 0 и 1, для которого h ₀(a ₃, …, a_n) = 1. Пусть h ₁ (a ₃, …, a_n) = a, h ₂(a ₃, …, a_n) = b, h ₃(a ₃, …, a_n) = c. Тогда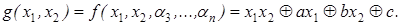

Построим функцию:

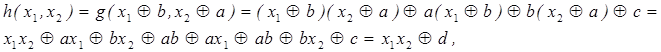где d = ab Å c. Если d = 0, то h (x ₁, x ₂) = x ₁ x ₂. Если d = 1, то h (x ₁, x ₂) = x ₁ x ₂ Å 1 и тогда 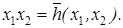Лемма доказана.

Функция f (x ₁,..., x _n) сохраняет константу a Î {0, 1}, если f (a, …, a) = a.

Пример 4. Функция xy сохраняет 0, сохраняет 1. Функция x ® y сохраняет 1 и не сохраняет 0.

Дата добавления: 2014-12-27