
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы изображения состава трёхкомпонентных систем
|
|
|
|
Способы изображения состава бинарных систем.
Схема фазовых превращений двух- и многокомпонентных систем.
С появлением в системе двух и более компонентов в закономерностях фазовых изменений возникают свои особенности.
В уравнениях состояния двухкомпонентных систем число независимых переменных равно четырём: T, p, c1, c2. Таким образом, для построения полной диаграммы состояния необходимо располагать системой координат четырёх измерений. В этих координатах диаграмма должна представлять собой совокупность поверхностей, расположенным некоторым образом в четырёхмерном пространстве. Подобное построение невозможно, и это вынуждает прибегать к некоторым упрощениям, вернее, к использованию таких переменных, описывающих состояние системы, которые позволяют сделать необходимое упрощение.
С этой целью вместо переменных T, p, c1, c2 переходим к переменным T, p, мольному объёму V и мольной доле первого компонента x1. Мольная доля второго компонента x2 при этом уже не может быть величиной независимой, она равна 1-x1.
Поскольку по всем трём осям трёхмерной диаграммы откладываются значения независимых переменных, каждая точка внутри этой диаграммы имеет физический смысл. Всё пространство объёмной диаграммы разделено поверхностями раздела на области, охватывающие такие сочетания значений T, p, x1, при которых могут существовать отдельные фазы.
В практической повседневной работе пользуются ещё более упрощёнными диаграммами, а именно сечениями объёмной диаграммы плоскостями, отвечающими постоянному давлению или постоянной температуре. Поскольку нам в наших исследованиях приходится часто иметь дело с превращениями, протекающими при постоянном давлении или при постоянной температуре, подобные сечения вполне удовлетворяют многие потребности теории и практики.
Состав трёхкомпонентной системы удобно изображать, пользуясь концентрационным треугольником. Вершины равностороннего треугольника отвечают содержанию в системе 100 % каждого из компонентов А, В и С. Стороны треугольника позволяют описать составы двухкомпонентных систем А+В, В+С, С+А.
Точки, лежащие внутри треугольника, описывают составы трёхкомпонентных систем.
Метод определения состава, предложенный Гиббсом, основан на том, что сумма перпендикуляров, опущенных из любой точки внутри равностороннего треугольника на каждую из сторон, равна высоте треугольника.
Фазовое поведение трёхкомпонентных углеводородных смесей в ряде случаев может быть корректно смоделировано посредством представления этих смесей как псевдобинарные. Многокомпонентная смесь приводится к псевдобинарной специальным образом. Трёхкомпонентная смесь получается смешением одного чистого компонента и бинарной смеси двух других компонентов. В случае четырёхкомпонентной смеси смешиваются бинарные смеси.
Указанный метод, применимый к любой многокомпонентной системе, для наглядности изложения применим к трёхкомпонентным смесям. Условие представления трёхкомпонентной смеси как псевдобинарная, вытекает из метрических свойств концентрационного треугольника (рис.1). Точки, отвечающие составу рассматриваемого раствора и образующих его смесей (А, В, С), должны лежать на одной прямой линии: секущей концентрационного треугольника, выходящей из вершины, соответствующей чистому наиболее высококипящему компоненту (К3 на рис.1).
При изменении состава тройного раствора по секущей молярные доли 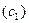 и
и 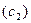 компонентов К1 и К2 зависят от молярной доли
компонентов К1 и К2 зависят от молярной доли 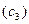 компонента К3 следующим образом:
компонента К3 следующим образом:
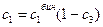 и
и 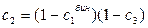 , (1)
, (1)
где 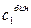 - молярная доля компонента К1 в исходной бинарной смеси
- молярная доля компонента К1 в исходной бинарной смеси 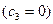 .
.
Условия фазового равновесия в трёхкомпонентной системе могут быть описаны, как показано в [4], уравнениями по форме аналогичными уравнениям, выражающим условия фазового равновесия в бинарных смесях. Это заключение может быть распространено на системы с числом компонентов больше трёх, поскольку любой многокомпонентный раствор может рассматриваться как продукт смешения одного чистого компонента и сложного «компонента», представляющего собой определённую смесь всех остальных компонентов рассматриваемой системы.
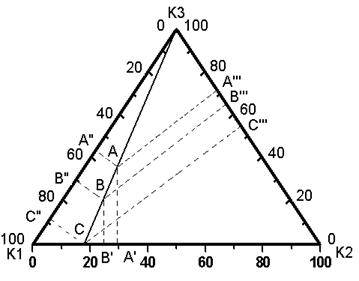
Рис. 1. Концентрационный треугольник для выражения состава трёхкомпонентной системы
На рис. 4, а приведена зависимость «объем — давление» для смеси пентана и гептана с массовой концентрацией последнего 52,4%.
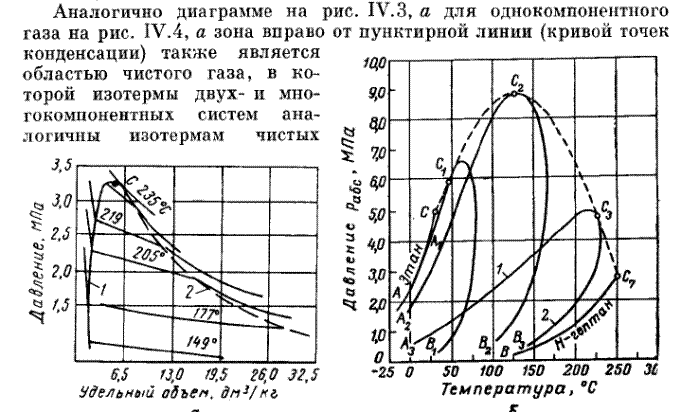
Рис. 4. Диаграммы фазового состояния двухкомпонентных систем.
а — зависимость «давление - удельный объем» для смеси н-пентана и н-гептана, содержащей 52,4% по массе н-гептана; б — диаграмма «давление — температура» для смесей этана с н-гептаном (точки C1, С2 и C3 - критические точки смесей, содержащих соответственно 90,22, 50,25 и 9,8% по массе этана); 1 —линия точек начала парообразования; 2 —линия точек росы.
компонентов. Влево от кривой точек парообразования изотермы жидкой фазы круто возрастают с уменьшением объема и они также аналогичны изотермам области жидкости чистых компонентов. В двухфазной же области двух- и многокомпонентных систем имеются значительные изменения. В области двухфазного состояния чистых углеводородов изотермы характеризуются горизонтальными линиями, т. е. давление не изменялось до полной конденсации газа (рис. 3).
Для двух- и многокомпонентных систем, как это следует из рис. 4а, давление в процессе сжатия в двухфазной области не остается постоянным и для конденсации газа необходимо повышать его для полного превращения газовой фазы в жидкость. Поэтому давление точки парообразования (кипения) для двух- и многокомпонентной смеси выше точек конденсации. В соответствии с этим не одинаков и состав жидкой и газовой фаз в точках парообразования и конденсации. Вскоре после начала конденсации газа состав последнего еще близок к составу всей системы. Точно так же вблизи точки парообразования состав жидкой фазы близок к составу исходной смеси. В двухфазной же области состав жидкой и газовой фаз отличен от состава исходной смеси и он непрерывно изменяется в соответствии с давлением и объемом системы.
Бинарные и многокомпонентные системы также имеют свои особенности и в области, лежащей вблизи критических давлений и температур. Критическая точка чистых веществ (или однокомпонентных систем) характеризуется самыми высокими давлениями и температурой, выше которых невозможно одновременно существование двух фаз — жидкой и газообразной. В бинарных и многокомпонентных системах критическая точка характеризуется лишь одинаково интенсивными свойствами газовых и жидких фаз. При этом в зоне пересечения кривых точек конденсации и парообразования образуется область, в которой могут существовать две фазы даже при температурах и давлениях, превышающих критические значения.
С появлением в системе второго компонента большие различия появляются также в диаграммах «давление - температура». Кривые точек начала кипения и точек росы не совпадают и образуют фазовую диаграмму, на вид которой, кроме температуры и давления влияет исходный состав смеси. Крайние левая и правая кривые на диаграмме (рис. 4б) соответствуют давлениям насыщенного пара для чистых компонентов — этана и н-гептана с критическими точками 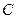 и
и 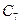 . Между ними расположены фазовые диаграммы смесей этана с н-гептаном с массовой концентрацией этана 90, 22; 50, 25 и 9,8% с соответствующими критическими точками
. Между ними расположены фазовые диаграммы смесей этана с н-гептаном с массовой концентрацией этана 90, 22; 50, 25 и 9,8% с соответствующими критическими точками 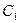 ,
, 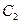 и
и 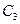 . Пунктирная линия представляет собой огибающую критических точек системы этан — н-гептан. Линии
. Пунктирная линия представляет собой огибающую критических точек системы этан — н-гептан. Линии 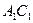 ,
, 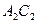 и
и 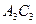 представляют собой линии точек начала кипения рассматриваемых смесей (выше и слева от них смесь находится в жидком состоянии),
представляют собой линии точек начала кипения рассматриваемых смесей (выше и слева от них смесь находится в жидком состоянии), 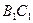 ,
, 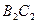 и
и 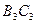 - линии точек росы соответствующих смесей. Ниже и справа от этих линий смесь находится в газообразном состоянии. Между линиями точек начала кипения и точек росы располагается двухфазная область. Из рис. 4, б видно, что с увеличением содержания н-гептана в системе критическая точка, располагающаяся слева от максимальных значений давления и температуры, при которых две фазы могут существовать в равновесии, сдвигается вправо от нее. Кривые же точек росы и начала кипения при этом приближаются к кривой давления насыщенного пара, преобладающего в смеси компонента - н-гептана. Аналогично изменяются также критические температуры и давления при изменении состава смеси.
- линии точек росы соответствующих смесей. Ниже и справа от этих линий смесь находится в газообразном состоянии. Между линиями точек начала кипения и точек росы располагается двухфазная область. Из рис. 4, б видно, что с увеличением содержания н-гептана в системе критическая точка, располагающаяся слева от максимальных значений давления и температуры, при которых две фазы могут существовать в равновесии, сдвигается вправо от нее. Кривые же точек росы и начала кипения при этом приближаются к кривой давления насыщенного пара, преобладающего в смеси компонента - н-гептана. Аналогично изменяются также критические температуры и давления при изменении состава смеси.
Величина критической температуры различных смесей находится между критическими температурами компонентов. По имеющимся экспериментальным данным для ее вычисления можно использовать свойство аддитивности (расчетные значения критических температур при этом получаются более близкими к действительным при выражении состава в процентах по массе, а не в молярных).
Критическое же давление смеси обычно выше, чем критическое давление чистых компонентов, кроме тех случаев, когда в смеси один из компонентов содержится в значительном количестве (т. е. правило аддитивности для вычисления 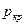 смеси нельзя применять). Отклонение фактической величины
смеси нельзя применять). Отклонение фактической величины 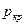 от вычисленного критического давления по правилу аддитивности возрастает с увеличением разницы между молекулярными массами чистых компонентов. Наибольшее критическое давление обычно наблюдается у смеси с близким массовым содержанием обоих компонентов.
от вычисленного критического давления по правилу аддитивности возрастает с увеличением разницы между молекулярными массами чистых компонентов. Наибольшее критическое давление обычно наблюдается у смеси с близким массовым содержанием обоих компонентов.
Как видно из рис. 4, б, размеры двухфазной области также зависят от состава смеси — они возрастают по мере того, как в составе смеси распределение между компонентами становится более равномерным.
Естественные углеводородные смеси отличаются большим разнообразием состава. Поэтому фазовые диаграммы нефтегазовых смесей, сохраняя принципиальные черты фазовых переходов двухкомпонентных систем, обладают еще своими в основном количественными особенностями, зависящими от состава нефти и газа.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1830; Нарушение авторских прав?; Мы поможем в написании вашей работы!