Одновыборочные тесты

Эти тесты служат для проверки соответствия распределения выборки заданному.

5.1.1. Тест Хи-квадрат

Критерий Хи-квадрат основан на статистике

,

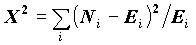где - ожидаемая частота i -го значения переменной, N_i расчетная. Теоретическое распределение этой статистики при больших N совпадает с распределением Хи-квадрат. Число степеней свободы теоретического распределения полагается равным k-1, где k - число значений исследуемой переменной. Эмпирическое правило говорит о том, что некорректно применять критерий, если ожидаемые частоты меньше 5, поскольку его распределение в этом случае не будет близко к теоретическому. Но использование точных методов вычисления значимости (метод Монте-Карло) позволяет избежать этого ограничения.

Пример. Пусть, согласно статистическим данным, 30% трудоспособного населения имеют возраст до 30 лет, 30% - от 30 до 40 лет и 40% свыше 40 лет. Соответствует ли выборочное распределение признака "возраст" в обследовании "Курильские острова" распределению возраста в генеральной совокупности?

RECODE v9 (1 THR 30 =1)(31 THR 40 =2)(41 THRU HI =3) INTO w9.

NPAR TESTS /CHISQUARE = W9 /EXPECTED 3 3 4.

Подкоманда /CHISQUARE задает тестируемую переменную; в подкоманде /EXPECTED задаем через пробел ожидаемые пропорции распределения.

Выполнение этих команд позволяет получить значение критерия и оценить степень соответствия нашей выборки распределению генеральной совокупности (табл. 5.1, 5.2).

Таблица 5.1. Наблюдаемые и ожидаемые частоты

	Observed N	Expected N	Residual
			-35
Total

Таблица 5.2. Статистика хи-квадрат

	W9
Chi-Square	8.333
Df
Asymp. Sig.	0.016

Анализируя таблицу 5.1, уже по отклонениям расчетных значений от ожидаемых (см. столбец RESIDUAL), видим, что эмпирическое распределение сильно отличается от теоретического. Достаточно высокое значение критерия (Chi-Square =8.333, таблица 5.2) мало информативно. Ответ о совпадении нашего распределения с теоретическим заключен в анализе наблюдаемого уровня значимости. Его малая величина (Asymp. Sig. =0.016) показывает, что полученные отклонения значимы: вероятность получить большие значения Хи-квадрат равна 1.6%, гипотеза о соответствии выборки указанной генеральной совокупности может быть отвергнута на уровне значимости 5%.

Таким образом, для данного случая тест показал существенное различие теоретического и эмпирического распределений.

Приведем пример применения метода статистического моделирования Монте-Карло. В этом примере производится 100000 экспериментов по моделированию выборки из генеральной совокупности с заданными вероятностями (p₁=0.3, p₂=0.3, p₃=0.4):

NPAR TEST /CHISQUARE=w9 /EXPECTED=3 3 4 /METHOD=MC CIN(99) SAMPLES(100000).

Естественно при такой большой выборке был получен тот же результат (таблица 5.3). Уровень значимости этим методом оценивается приближенно, на основе статистических экспериментов - чем больше экспериментов, тем точнее. Поскольку оценка значимости получена на основе случайных экспериментов, выдается доверительный интервал для уровня значимости (99%-й по умолчанию). Точечная оценка наблюдаемого уровня значимости (Monte Carlo Sig) совпадает с асимптотической оценкой (Asymp. Sig., табл.5.3), "оптимистическая" нижняя граница равна 0.015, "пессимистическая" верхняя - 0.017. Таким образом, со всех точек зрения отклонение распределения значимо.

Таблица 5.3. Значимость критерия хи-квадрат

			W9
Chi-Square			8.333
Df
Asymp. Sig.			0.016
Monte Carlo Sig	Sig.		0.016
	99% Confidence Interval	Lower Bound	0.015
		Upper Bound	0.017

5.1.2. Тест, основанный на биномиальном распределении

Проверяется гипотеза о параметре биномиального распределения H₀: p=p₀. Например, проверим по нашей выборке, действительно ли в генеральной совокупности вероятность встретить мужчину p=0.5,, а молодежь не старше 30 лет - с вероятностью p=0.3 (см. предыдущий пример):

NPAR TESTS BINOMIAL(0.5) = V8(1,2).

NPAR TESTS BINOMIAL(0.3) = V9(30).

В скобках за ключевым словом BINOMIAL указывается вероятность "успеха". Далее следует тестируемая переменная. Если за ней в скобках следует два значения, то считается, что выборка ограничена двумя группами, соответствующими этим значениям, а успех соответствует первому значению. Если в скобках задано одно значение, то успех - принятие переменной значения, не большего этого числа. В диалоговом окне есть возможность задать как "точку разрыва", так и два кода.

Программа подсчитывает число объектов m, имеющих заданные значения (в первом случае m - число мужчин (код 1), во втором случае m - число респондентов не старше 30 лет). На основании свойств биномиального распределения подсчитывается двусторонняя наблюдаемая значимость - вероятность случайной величины в условиях биномиального распределения с параметром P отклониться от ожидаемого значения np больше, чем отклонилось выборочное значение m.

Наблюдаемый уровень значимости можно оценить с использованием теоремы Муавра-Лапласа, методом Монте-Карло, а также точно, по биномиальному распределению, используя возможность, представленную в SPSS в EXACT STATISTICS:

NPAR TEST /BINOMIAL (.50)= v8 /METHOD=EXACT TIMER(5).

Таблица 5.4. Значимость критерия хи-квадрат

	Category	N	Observed Prop.	Test Prop.	Asymp. Sig. (2-tailed)	Exact Sig. (2-tailed)
Group 1	1 муж.		0.508	0.5	0.708	0.708
Group 2	2 жен.		0.492
Total

В таблице 5.4 выдается расчетная 0.508 и заданная теоретическая вероятность Test Prop.=0.5. Выборочное распределение почти совпало с заданным. Этот результат окончательно подтверждает величина двусторонней значимости: 0.708 - вероятность случайно получить значение, большее полученного. Так как 70% - это большая вероятность, мы делаем вывод, что распределение совпадает с заданным. Двусторонний тест показал незначимое отличие доли мужчин в выборке от ожидаемой доли (нулевая гипотеза не отвергается).

5.1.3. Тест Колмогорова-Смирнова

Одно-выборочный тест предназначен для проверки гипотезы о распределении в генеральной совокупности. Статистика критерия - абсолютная величина разности эмпирической и теоретической функций распределения:

Команда задания теста Колмогорова-Смирнова имеет вид:

NPAR TESTS K-S(NORMAL,5,2)=X.

В скобках за ключевым словом K-S указывается предполагаемый вид распределения: NORMAL - нормальное; UNIFORM - равномерное; POISSON - распределение Пуассона; EXPONENTIAL - показательное распределение. За видом распределения в скобках можно указать его параметры: для нормального - среднее и среднеквадратичное отклонение; для равномерного - минимум и максимум; для распределения Пуассона - среднее. По умолчанию используются оценки параметров по выборочной совокупности.

Заметим, что оценка параметров по выборке дает смещение этого критерия. Поэтому ему стоит доверять только для больших выборок.

Таблица 5.5. Проверка нормальности распределения доходов с использованием критерия Колмогорова-Смирнова.

		V14 Душевой доход в семье
N
Normal Parameters	Mean	229.11
	Std. Deviation	151.34
Most Extreme Differences	Absolute	0.187
	Positive	0.187
	Negative	-0.149
Kolmogorov-Smirnov Z		4.85
Asymp. Sig. (2-tailed)

В таблице результатов выдается двусторонняя значимость - вероятность случайно в условиях гипотезы превзойти выборочное значение статистики, фиксирующей отличие распределения от заданного.

Например, проверим нормальности распределения доходов командой:

NPAR TESTS K-S(NORMAL) = V14.

Поскольку двусторонняя значимость в таблице 5.5 (2-tailed P) равна нулю, то можем сделать вывод, что полученная разность фиксирует существенное отличие распределения по доходам от нормального. Во многих исследованиях используется вместо дохода используется его логарифм, распределение которого считается близким к нормальному. Проверим нормальность логарифма доходов:

compute lnv14=ln(v14).

npar test k-s(normal)=w14.

Таблица 5.6. Проверка лог-нормальности распределения доходов

		LNV14
N
Normal Parameters	Mean	5.2812
	Std. Deviation	0.5344
Most Extreme Differences	Absolute	0.098
	Positive	0.098
	Negative	-0.055
Kolmogorov-Smirnov Z		2.54
Asymp. Sig. (2-tailed)

Значение критерия несколько уменьшилось, но существенность различия сохранилось (таблица 5.6).

Иногда бывает необходимо проверить законы распределения не предусмотренные в NPAR TESTS. В этом случае вспомните, что распределение непрерывной случайной величины h =Fx (x), где F - функция распределения x, равномерно на отрезке (0,1). Таким образом, воспользовавшись статистическими функциями преобразования данных SPSS, из тестируемой переменной можно всегда получить переменную, имеющую теоретически равномерное распределение и проверив, действительно ли ее распределение равномерно, принять или отвергнуть гипотезу о виде распределения Fx (x).

5.2. Тесты сравнения нескольких выборок

Эти тесты предназначены для проверки гипотезы совпадения распределений в выборках. В отличие от t -теста и известных методов дисперсионного анализа, здесь не предполагается нормальность теоретического распределения.

Многие тесты основаны на поиске определенного типа противоречия с гипотезой совпадения распределений и не может обнаружить всех отличий. Например, тест медиан проверяет совпадение только медиан. Поэтому иногда полезно воспользоваться несколькими тестами.

5.2.1. Двухвыборочный тест Колмогорова-Смирнова

Двухвыборочный тест Колмогорова-Смирнова предназначен для проверки гипотезы о совпадении распределений в паре выборок:

NPAR TESTS K-S=V14 BY V4(1,3).

В команде за ключевым словом K-S следует тестируемая переменная (в нашем примере - V14), за ней после слова BY указываются сравниваемые группы - переменная, определяющая эти группы, и соответствующие этим группам значения: V4(1,3).

Статистика критерия - абсолютная величина разности эмпирических функций распределения в указанных выборках:

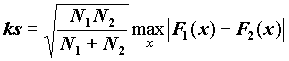, где N₁ и N₂ - объемы выборок.

В листинге выдается статистика критерия Z=ks двусторонняя значимость - вероятность случайно в условиях гипотезы превзойти выборочное значение статистики.

Пример: сравнение распределений доходов групп готовых отдать острова или их часть и придерживающихся твердой позиции:

recode v4(1,2=1)(3=2) into W4.

Var lab W4 "отношение к передаче островов".

Val lab 1 "Отдать" 2 "нет".

npar test k-s=v14 by w4(1,2).

Таблица 5.7. Cравнение распределения доходов в двух группах на основе критерия Колмогорова-Смирнова,.

		V14 Душевой доход в семье
Most Extreme Differences	Absolute	0.05
	Positive	0.05
	Negative	-0.028
Kolmogorov-Smirnov Z		0.455
Asymp. Sig. (2-tailed)		0.986

В приведенном примере (таблица 5.7) наблюдаемый уровень значимости велик (0.986). Поэтому, приходим к заключению, что на нашей учебной выборке критерием Колмогорова-Смирнова не удалось обнаружить различие распределений по душевому доходу в группах считающих, что нужно отдать острова или их часть, и противников такого решения. Это не означает достоверно, что распределения совпадают, возможны тонкие различия распределений, которые критерий не улавливает из-за малого объема данных.

5.2.2. Тест медиан

Этот тест позволяет сравнивать распределения исследуемой переменной сразу в нескольких группах. Тест весьма груб, но прост.

NPAR TESTS MEDIAN = V14 BY V1(1,3).

Внешне задание теста похоже на задания критерия Колмогорова-Смирнова.

Задание сравниваемых групп. После слова BY за именем переменной в скобках указывается интервал значений. В приведенном примере сравниваются распределения в трех группах. Тестом можно сравнить также и пару групп, если в скобках вначале указать большее значение, затем меньшее (при задании V4(3,1) сравниваются только 1-я и 3-я группы).

Суть проверки гипотезы состоит в следующем. Значения исследуемой переменной (в нашем примере - V14) делятся на две группы: больше медианы и меньше или равно медиане. Такое разделение можно считать заданием новой, дихотомической переменной. Вычисляется таблица сопряженности полученной дихотомической переменной и переменной, задающей группы. Далее применяется известный критерий Хи-квадрат. Если величина наблюдаемой значимости критерия мала, естественно предположить, что распределение исследуемой переменной в группах различается существенно.

Замечание. Для получения дихотомии можно, также, навязать точку "разрыва" переменной, не совпадающую с медианой, указав в скобках за словом MEDIAN соответствующее значение.

Пример. Курильское обследование проходило в 21 городе Западной Сибири. Экспертным путем все города разделены на 4 типа: 1 растущие, 2 стабильные, 3 крупные, 4 гиганты. Типу города в наших данных соответствует переменная TP.

Исследуется связь доходов и типа населенного пункта.:

npar test med=v14 by TP(1,4).

Таблица 5.8. Метод медиан. Разделение на две подвыборки.

		TP тип поселения
		Растущие	Стабильные	крупные	гигант
V14 Ср.мес. душевой доход в семье	> Median
	<= Median

Таблица 5.9. Метод медиан. Значимость критерия.

	V14 Ср.мес. душевой доход в семье
N
Median
Chi-Square	28.698
Df
Asymp. Sig.

Анализируя величину наблюдаемой значимости, видим, что между точкой зрения на иностранную помощь и возрастом имеется существенная связь, т.е. обнаружено значимое различие распределения доходов в группах.

Дата добавления: 2014-12-27