Численные методы анализа

NEXT

PRINT y$ Результат: “еинаминВ“

Здесь в переменной y$ формируется нужный результат.

Тест. 2.7.1. Чему будет равно Х после завершения программы? 1). 456128, 2).561234, 3).341285.

y$=”123456”

x$= RIGHT$(y$,3)+LTRIM$(STR$(VAL(LEFT$(y$,3))+5))

Важнейшая область приложения программирования – инженерные расчеты. Здесь широко используются методы вычислительной математики. Рассмотрим некоторые из популярных численных методов.

¶Вычисление определенного интеграла. Аналитическое интегрирова­ние возможно лишь для небольшого класса “табличных” функций. В других случаях приходится прибегать к приближенным методам. Нахождение определенного интеграла заключается в вычислении площади под подинтегральной функцией в заданном диапазоне аргумента. Самый простой, но и самый грубый метод – метод прямоугольников (рис. 2.8.1).

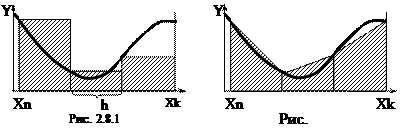Здесь диапазон интегрирования от начальной точки Xn до конечной Xk разбивается на небольшие участки (всего N участков) с основанием h. Сумма площадей всех участков (Y(Xi)*h) и будет считаться интегралом.

Xk n–1

S = ò Y(x)dX» åY(X i )*h

Xn i=1

Приближенным значением интеграла S считаем сумму площадей всех прямоугольников под кривой (на рисунке заштрихованы). Видим, что погрешность метода весьма велика. Более точным является метод трапеций (рис. 2.8.2). Площадь элементарной трапеции (h[Y(Xi)+Y(Xi+h)]/2) гораздо лучше приближа­ется к кривой.

Программа (для функции Y=X2), реализующая оба метода, приведена ниже.

h=0.1: s=0 'задание шага h

Xn = 0: Xk = 5 'задание пределов интегрирования

FOR x = Xn TO Xk- h STEP h 'изменение текущих точек

's=s+h*x^2 'метод прямоугольников

s=s+h*(x^2+(x+h)^2)/2 'метод трапеций

Дата добавления: 2014-12-27