Часть 2 2 страница

изнасилования — 164/154723=0,00106;

разбои — 3035/154723=0,019616;

грабежи — 19985/154723=0,129166;

кражи — 63505/154723=0,410443;

прочие преступления — 64449/154723=0,416544.

Результаты расчетов сведем в таблицу, переводя найденные значе­ния в проценты и округляя их до десятых.

Структура зарегистрированной преступности по видам
(Свердловская область, 2005 г.), %

Убий­ства и покуше­ния на убийства	Причи­нение тяжкого вреда здо­ровью	Изнаси­лования	Разбои	Грабежи	Кражи	Прочие преступ­ления
0,8	1,6	0,1	2,0	12,9	41,0	41,7

Наряду с соотношением части и целого используют соотношение между двумя частями одного целого.

Относительные величины, характеризующие соотношение между частями одного, называют относительными величинами координации (ОВК).

ОВК показывает, в какой степени одна из частей больше или меньше другой. Например, в Свердловской области в 2005 году зарегистрировано случаев причинения тяжких телесных повреждений в 2,1 раза больше (2421/1164), чем убийств с покушениями на убийство.

Относительные величины интенсивности

Отношение части к целому, или отношение интенсивности, представляет собой обобщающую относительную величину, ко­торая позволяет выявить степень распространенности определенного при­знака в среде его распространения.

Относительная величина интенсивности рассчитывается как отноше­ние величины явления к размеру среды, которая является его базой:
(показатель явления А)/(показатель размера среды распространения явления А).

Относительная величина интенсивности характеризует степень развития явления в среде его распространения: сколько единиц числителя приходится на 1, 10, 1000 и т.д. единиц знаменателя (например, при определении уровня рождаемости рассчитывается число родившихся на 1000 человек населения, при определении плотности населения рассчи­тывается число людей, приходящихся на 1 кв. км территории). Определя­ется как отношение двух абсолютных разноименных величин и выража­ется именованным числом, включающим наименование величин измеряе­мого признака и среды его распространения.

В уголовно-правовой статистике рассчитывается коэффициент преступности как отношение фактов преступлений или числа лиц, их совершивших, к численности населения, достигнувшего возраста, с кото­рого наступает уголовная ответственность.

Формула для расчета коэффициента преступности (на 10 тыс. человек населения):

,

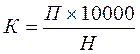где К – коэффициент преступности;

П – число преступлений или число лиц, их совершивших;

Н – численность населения в возрасте 14 лет и старше.

Коэффициент преступности может исчисляться как в фактах (престу­плениях), так и в лицах (субъектах преступлений). В первом случае в числитель П необходимо включить все зарегистрированные, в том числе и нераскрытые преступления. Во втором случае в числитель включают не только число осужденных, но и число освобожденных от уголовной ответ­ственности по нереабилитирующим основаниям (например, по амнистии).

При малых числах преступлений и на­селения (в городе, районе, на предприятии) коэффициент преступности может рассчи­тываться на 100 тыс. жителей. Однако в любом случае эти числа означают размерность коэффициента и обязательно указываются.

Ввиду отсутствия зачастую сведений о населении по возрастной категории 14 – 16 лет по отдельным территориям (субъектам Федерации, районам, городам и т.д.) на практике вычисляют коэффициенты преступ­ности и судимости по отношению ко всему населению данной территории.

Для примера рассчитаем коэффициент преступности на 10 тыс. человек населения в Свердловской области по данным за 2005 год, исходя из среднегодовой численности населения области 4 318 000 человек:

.

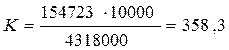При расчете коэффициента преступности необхо­димо знать некото­рые особенности.

– Численность населения всегда приводится на определенную дату (обычно на нача­ло или конец года). Коэффициент интенсив­ности обычно рас­считывают на численность населения по состоянию на конец года или среднегодовую численность населения, которая берется в виде полусуммы численности населения в начале и конце года.

– Демографы различают население постоянное и наличное. Для регионов с высоким уровнем вре­менного населения при расчете коэффициентов интенсив­ности этого нельзя не учитывать, особенно в криминологии, так как временные жители совершают достаточно большое число преступлений.

– В криминологических исследованиях вместо общего числа уч­тенной преступности при расчете коэффициента может быть взято общее число раскрытых преступлений, выявленных правонару­шителей, предварительно арестованных, всех осужденных, осуж­денных к лише­нию свободы, заключенных, потерпевших и др. В этом случае имеют дело с числом раскрытых преступ­лений на 100 тыс. жителей, с числом выявленных правонаруши­телей, с числом потерпевших (коэффициент виктимизации) или с числом заключенных на ту же численность населе­ния и т. д.

– Коэффициент преступности может быть рассчитан в от­ношении несовер­шеннолетних, женщин, мужчин, ранее суди­мых, безработных, студентов, военнослужащих и других групп населения по той же формуле. Только в этом случае символ «П» будет означать число преступлений, совершенных изучаемой груп­пой граждан, а символ «Н» — общее число граждан данной ка­тегории в стране, регионе, городе.

– Для объективной оценки уровня отдельных групп и видов прес­туплений рассчитывается коэффициент насильственных, ко­рыстных, эко­номиче­ских деяний или умышленных убийств, из­насилований, краж и т. д.

Совокупность различных коэффициентов помогает более объективно оценивать уровень преступности и ее видов и срав­нивать их во времени (по годам) и в пространстве (по террито­риям).

Относительные величины динамики

Относительные величины динамики показывают, во сколько раз увеличился (или уменьшился) уровень показателя текущего периода по сравнению с базисным периодом.

Этот вид относительных величин имеет самое широкое распро­стра­нение в различных отраслях статистики. В правовой статистике относи­тельные величины динамики применяют при анализе изменений преступ­ности — движении общего числа преступлений и их отдельных категорий, динамики нагрузки следователей, судей и т.д.

За временной интервал обычно принимается год. Но измене­ние преступности и других юридически значимых явлений может отслежи­ваться по пятилетиям, что сглаживает их динамику, по кварталам, месяцам и даже дням, что дает возможность выявить все имеющиеся колебания.

В качестве базисного периода может использоваться период, который был чем-то характерен для изучаемого явления. Например, при изу­чении гражданско-правовых явлений таким базовым годом может быть год вступления в действие той или иной части нового Гражданского кодекса, при изучении уголовно-правовых яв­лений — год вступления в действие Уголовного кодекса, кото­рый впервые криминализировал значи­тельное число новых со­ставов. В этом случае при вычислении относи­тельных величин динамики сопоставление производится по отношению к одному и тому же значению показателя базисного периода. Такие ве­личины называются относительными величинами с неподвижной базой. Они применяются в тех случаях, когда есть необходимость постоянного наблюдения за развитием изучаемых явлений по сравнению с периодом, имеющим почему-либо особо важное для подобного сравнения значение.

Задачи ста­тистического анализа часто требуют ежегодных (или по иным пе­риодам) сопоставлений, когда за базу принимаются данные каж­дого предыдущего года (месяца или другого периода). Такие отно­ситель­ные показатели называются величинами, вычисляемыми цепным спосо­бом. Подобная база называется подвижной.

Данные, характеризующие динамику явлений, чаще всего приво­дятся в виде статистического временного ряда, в котором по годам (или другим пе­риодам) приводятся значения того или иного показателя в абсолютных именованных числах. Эти абсолютные значения называют уровнями ряда.

При анализе динамических рядов вы­числяют следующие величины:

абсолютный прирост (снижение) — разность меж­ду уровнями ряда анализируемого и базисного;

темп рос­та (снижения) — отношение уровня ряда анализируемого периода к уровню ряда базисного периода;

темп прироста (снижения) — отношение абсолютного приро­ста анализируемого периода к уровню ряда базисного периода.

Темпы роста и темпы прироста выражаются в процентах, реже в виде простых отношений, называемых коэффициентами роста.

В качестве примера рассчитаем абсолютный прирост, темпы роста (снижения) и темпы прироста (снижения) числа зарегистрированных преступлений в Свердловской области в период 2001 – 2005 гг., используя подвижную базу.

Характеристика
1.Число преступлений (уровень ряда)
2.Абсолютный прирост по сравнению с предыдущим годом (подвижная база)	-	90596-121108= = -30512	106979-90596= =16383	119987-106979= =13008	154723-119987= =34736
3.Годовой темп роста (снижения) (подвижная база), %	100,0	90596/ 121108* 100=74,8	106979/ 90596* 100=118,1	119987/ 106979* 100=112,2	154723/ 119987* 100=128,9
4.Годовой темп прироста (сни­жения) (подвижная база), %	0,0	-30512/ 121108* 100= -25,2	16383/ 90596* 100=+18,1	/106979* 100=+12,2	34736/ 119987* 100=+28,9

Выполним те же расчеты с использованием неподвижной базы, принимая за базисный период 2001 год.

Характеристика
1.Число преступлений (уровень ряда)
2.Абсолютный прирост по сравнению с 1996 г. (неподвижная база)	-	90596-121108= = -30512	106979-121108= =16383	119987-121108= =13008	154723-121108= =34736
3.Темп роста (снижения) к 1996 г. (неподвижная база), %	100,0	90596/ 121108* 100=74,8	106979/ 121108* 100=118,1	119987/ 121108* 100=112,2	154723/ 121108* 100=128,9
4.Темп прироста (снижения) к 1996 г. (неподвижная база), %	0,0	-15593/ 121108* 100= -14,5	-10703/ 121108* 100= -10,0	7807/ 121108* 100=+7,3	9274/ 121108* 100=+8,6

Из сравнения результатов расчетов темпов роста (снижения) и темпов прироста (снижения) видим, что между ними существует связь: в каждом периоде темп прироста (снижения) на 100% меньше соответст­вующего темпа роста (снижения).

Относительные величины выполнения плана

Относительная величина выполнения плана рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному.

Относительные величины степени и сравнения

Относительные величины сравнения — отношение ве­личины, характеризующей данный объект, к одноименной вели­чине по другому аналогичному объекту.

Обычно их исчисляют в процентах или кратных отношениях, показы­вающих, во сколько раз одна из сравниваемых величин боль­ше (или меньше) другой. Это может быть как отношение простран­ственного, так и отношение временного сравнения.

При помощи относительных величин степени и сравнения сопостав­ляются показатели по разным странам, регионам, предприятиям и т.д. Сравнение показателей про­изводства или уровня жизни в разных странах, зарегистрированных преступлений в разных регионах или в одном из них по разным вре­менным периодам (по кварталам, годам и т.д.), сравнение резуль­татов деятельности по тем или иным направлениям социального кон­троля над преступностью — это обычные приемы анализа.

При вычислении таких величин необходимо позаботиться, чтобы сравниваемые показатели определялись по единой методике, были сравнимы по единицам из­мерения и во всех других отношениях.

В качестве примера вычисления относительной величины степени и сравнения сравним удельные весы грабежей и разбоев в структуре зарегистрированной преступности Свердловской области в 2005 году, если их значения соответственно равны 12,9% и 2,0%. Разделив 12,9 на 2,0, получим, что в структуре зарегистрированной преступности Свердловской области в 2005 году удельный вес грабе­жей в 6,6 раза больше удельного веса разбоев.

К рассматриваемой группе относительных величин примыка­ют коэффициенты преступной активности или «пораженности» пре­ступно­стью различных групп населения. Они представляют собой соотношение доли определенной группы (половозрастной, соци­альной и т.д.) в составе контингента преступников и доли соот­ветствующей группы в составе всего условно взрослого населения (т.е. населения в возрасте, в котором возможна уголовная ответ­ственность) региона, «сформировавшего» данный контингент преступников. В этих коэффициентах находит отражение изве­стное теории криминологии и практике борьбы с преступ­ностью положение о том, что различные груп­пы населения неодинаково «поражаются» преступностью.

Коэффициент преступной активности показывает, насколько доля одного возрастного поколения преступников больше или мень­ше доли такого же поколения среди всего условно взрослого на­селения. При равенстве долей этих возрастных поколений коэф­фициент будет равен единице. Так, например, если среди осуж­денных доля мужчин возрастной группы 30—34 года составляет 0,25, а доля этого же поколения в составе населения — 0,20, то коэф­фициент преступной активности составляет 0,25:0,20 = 1,25. Этот показатель наглядно свидетельствует о превышении доли указан­ной половозрастной группы среди осужденных над долей такой же группы в составе условно взрослого населения и точно характе­ризует распространенность среди этой группы преступлений. При этом сразу фиксируется отклонение от «нормального», «стан­дар­т­ного» распро­странения преступности (когда коэффициент равен 1) среди конкретной группы и видна интенсивность распространения преступности в точном количественном выражении.

Индексы

В широком понимании слово «индекс» (от лат. index — указа­тель, список, реестр) означает любой обобщающий показатель, характеризую­щий изучаемое явление.

Индекс – это относительный показатель сравнения двух состояний одного и того же явления (простого или сложного), состоящего из соизмеримых или несоизмеримых элементов.

Сфера использования таких показателей широка: с их помощью характеризуется развитие национальной экономики в целом и ее отдель­ных отраслей, анализируются результаты про­изводственно-хозяйственной деятельности предприятий и органи­заций, исследуется роль отдельных факторов в формировании важнейших социально-экономических показа­телей, индексы ис­пользуются также в международных сопоставлениях социально-экономических показателей, определении уровня жизни и т.д. Примерами индексов являются: объем валового внутреннего продукта, индекс потребительских цен, индекс курса акций ведущих компаний (индекс Доу Джонса) и т.п.

В правовой статистике используется показатель-индекс состояния безопасности дорожного движения (индекс тяжести дорожно-транс­портных происшествий). Органы внутренних дел исчисляют тяжесть последствий дорожно-транспортных происшествий (ДТП) пу­тем отношения числа погибших к числу пострадавших в ДТП людей. Определенный по такой ме­тодике индекс тяжести ДТП за 2000 г., когда в России было совершено 157 596 ДТП, в которых погибло 29 468 человек и 178 378 человек ранено, составил 14,2 на 100 человек пострадавших: 29594*100/(29594+178378).

Ряды распределения абсолютных и относительных величин

Ряды распределения — это ряды абсолютных и относительных чисел, которые характеризуют распределение единиц совокупно­сти по атрибутив­но­му или количественному при­знаку.

Ряды распределения, построенные по количественному при­знаку (возраст, стаж, меры наказания, сроки расследования или рассмот­рения дел, число судимостей и т. д.), называются вариа­ционными рядами. Различия единиц совокупности (до 20 лет, 20 – 24 года, 25 – 29 лет и т. д.) количественного признака называется вариацией, а сам конкретный признак — вариантой.

Интервальный вариационный ряд может строиться с равны­ми интер­валами (20 — 24, 25 — 29 лет) или с неравными (14 – 15, 16 – 18, 19 – 20, 21 – 25 лет) ин­тер­ва­ла­ми. В первом случае оба интервала равны 5 годам, а во втором случае — 2, 3, 5 годам.

Статистический анализ вариационных рядов требует не только нали­чия частот (частостей), но и накопленных частот (частостей). Накопленная частота для той или иной варианты представляет собой сумму частот всех предшествующих вариант (интервалов). В примере для интервала 20 — 24 года накопленная частота будет равна: 2 + 18 = 20 человек, а накопленная час­тость 4 + 36 = 40%, а для интервала 25 — 29 лет соответственно: 2 + 18 + 10 = 30 человек, или 4 + 36 + 20 = 60%. Таким образом от варианты к варианте (от интервала к интервалу) идет накопление (кумуляция) частот и частостей.

Вариационные ряды легко изображаются графически в виде полиго­нов или гистограмм. Графическое изображение накоплен­ных частот (частостей) воспроизводится в системе прямоуголь­ных координат в виде кумуляты. По оси ординат откладывается вели­чина накопленных частот, а по оси абсцисс — воз­рас­та­ющие значения количественного признака. Накопленные частоты и кумулята — это интегральные показате­ли плотности распределения величины.

Примером распределения совокупности по атрибутив­но­му признаку может быть распределение сотрудников милиции (офи­церов) по званию: полковников — 1, подполков­ников — 3, майоров — 8... всего — 50 чело­век. Эта же совокуп­ность может быть распределена по количественному приз­наку, в частности, по возрасту: моложе 20 лет — 2, 20 — 24 года — 18, 25 — 29 лет — 10 и т. д.

В обоих примерах ряды распределения выражены в абсолютных числах, которые называются частотами ряда распределе­ния. Они указывают, насколько часто повторяется та или иная варианта (признак). Варианта «майор» имеет частоту 8, а варианта «20 — 24 года» — 18.

Ряды распределения в таблицах часто имеют и час­тоты, и частости:

Звание	Абсолют­ное число	В % к итогу	Возраст, лет	Абсолют­ное число	В % к итогу
Полковник Подполковник Майор Капитан Ст. лейтенант Лейтенант Мл. лейтенант			До 20 20-24 25-29 30-34 35-39 40-49 50 и старше
Итого 50	100,0	Итого 50	100,0

Если значения атрибутив­ных или количественных признаков выражены в относительных числах (например, в процентах к об­щему числу), то эти значения именуются частостями. В этом слу­чае наши примеры выглядят так: полковников — 2%, подпол­ковников — 6%, майоров — 16%... всего 100%; моложе 20 лет — 4%, 20-24 года — 18%, 25-29 лет — 10%... всего 100%.

Вопросы для самопроверки

1) В чем состоит основное различие между признаком и статистическим показателем?

2) Что выражают абсолютные показатели?

3) Что характеризуют относительные величины структуры?

4) Приведите примеры использования относительных величин структуры в уголовно-правовой статистике.

5) Как рассчитывается относительная величина интенсивности?

6) Что такое коэффициент преступности?

7) Укажите два подхода к вычислению коэффициента преступности.

8) Укажите область применения относи­тельных величин динамики в правовой статистике.

9) Что такое «подвижная база» при исчислении относи­тельных величин динамики?

10) Как вычислить темп роста(снижения) и темп прироста (снижения)?

11) Дайте определение относительных величин степени и сравнения.

12) Как исчисляют органы внутренних дел индекс тяжести дорожно-транспортных происшествий)?

13) Что характеризуют ряды распределения?

Тема 6. СРЕДНИЕ ВЕЛИЧИНЫ И ИХ ИСПОЛЬЗОВАНИЕ
В ПРАВОВОЙ СТАТИСТИКЕ

1 Понятие средней величины

С помощью средних величин можно сравни­вать совокупности яв­лений по тем или иным количественным признакам.

Средняя величина в статистике представляет собой обобщен­ную характеристику совокупности однородных явлений по како­му-либо одному количественно варьирующему признаку. Она все­гда обобщает количественную вариацию признака. За всякой средней скрыва­ется ряд рас­пределения единиц совокупности по изучаемому признаку, т. е. вариационный ряд.

Важнейшим условием расчета средних вели­чин является качествен­ная однородность единиц совокупности в отно­шении осредняемого признака. Средние величины, вычисленные для явлений разного типа, представляют собой фикцию. Средняя величина только тогда будет выражать типичный уровень признака, когда она рассчитана по качест­венно однородной совокупности. Статистические группировки иг­рают в этом отношении незаменимую роль. Поэтому в криминологии, социологии права и дру­гих юридических дисциплинах применяют, преимущественно, групповые средние, т. е. средние, вычисленные на основе статистических группировок.

Средние величины основываются на массовом обобщении фак­тов. Только при этом условии они способны выявить те или иные тенденции, лежащие в основе наб­лю­даемого явления. Средние величины отражают самую общую закономерность, прису­щую всей массе изучаемых явлений. Она проявляется в типичнойколичественной ха­рактеристике, т. е. в сред­ней величине всех име­ющихся (варьирующих) пока­за­те­лей.

Принципиальная суть статистического познания состоит в по­гашении случайного, вызванного действием индивидуальных при­чин, и в выявле­нии закономерностей, обусловленных общими при­чинами. Возможностью перехода от единичного к общему, от случай­ного к закономерному объяс­няется важность метода средних ве­личин и его широкое применение в аналитической работе при на­учно-практическом изучении правонарушений и государствен­ных мер социального контроля над ними.

Средняя величина всегда именованная, имеет ту же размерность (единицу измерения), что и признак у отдельной единицы сово­купности.

2 Виды средних величин

Выбор вида средней в конкретном случае зависит от характера свя­зи между величиной признака, по значениям которого вычисля­ется средняя.

При прямой пропорциональности между определяющим свой­ством и данным признаком, т.е. тогда, когда значения признака увеличиваются и уменьшаются с увеличением или уменьшением характеризуемых ими явлений, всегда применяется средняя ариф­метическая.

Средняя арифметическая

При изучении социально-правовых явлений наиболее часто ис­поль­зуются средняя арифметическая. Она может быть рассчитана по формуле для простой средней арифметической:

где x_i – i –тое значение признака (варианты), (i = 1,…, n);

n – число значений признака.

Средняя арифметическая вычисляется как сумма всех отдельных значений признака, деленная на число слагаемых n.

Для примера рассчитаем среднюю годовую нагрузку на одного судью, если годовая нагрузка 10 судей составила: 23, 37, 28, 41, 40, 39, 35, 40, 28 и 29 гражданских дел различной направленности. Сложив значения всех индивидуальных нагрузок и разделив полученную сумму на число судей, получим искомую величину:

В случаях, когда отдельные значения признака повторяются, средняя арифметическая вычисляется по формуле для взвешенной средней арифметической:

,

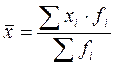где f_i – число повторений i –того значения признака (i = 1,…, n), называе­мое весом или частотой.

В качестве примера использования этой формулы определим сред­ний возраст осужденных в колонии для несовершеннолет­них, в которой содержится 1000 человек, распределившихся по возрас­тным группам следующим образом:

Возраст (варианты) Число лиц (вес каждого варианта)

15 120

16 150

17 200

18 530

Подставляя значения вариант и весов в формулу для расчета взвешенной средней арифметической, получим:

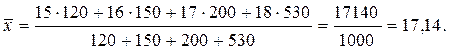
Средние величины могут вычисляться как на основе абсолют­ных величин, так и относительных показателей.

Средняя гармоническая

Иногда величина определяющего свойства бывает обратно пропор­циональна величине данного признака, что имеет место тог­да, когда значения признака уменьшаются при увеличении харак­теризуемых ими явлений или увеличиваются при уменьшении этих. При такой фор­ме связи между величиной определяющего свойства и величиной признака при­ме­няется средняя гармоническая.

Средняя гармоническая — это отношение числа вариантов признака к сумме обратных их значений. Она вычисляется по фор­муле:

,

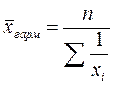где х_i – i –тое значение признака (варианты), (i = 1,…, n).

Средняя гармоническая довольно часто применяется для ана­лиза хозяйственной деятельности, когда величина определяющего свойства (сумма пла­нов) обратно пропорциональна величине данного признака (про­цент выполнения плана). Именно в таких случаях и необходимо применять формулу средней гармонической, которая равна обратному значению средней арифметической, вычисленной из обратных величин (обратная величина равна единице, деленной на прямую величину).

Средняя геометрическая

Этот вид средней вычисляется для установления средних по­казате­лей темпов роста рядов динамики, построенных с использованием подвижной базы.

Средняя геометрическая исчисляется путем извлечения корня степени n из произведений всех отдельных значений признака:

.

Воспользуемся этой формулой для расчета среднегодового темпа роста (снижения) числа зарегистрированных преступлений в Свердлов­ской области в период с 2001 по 2005 гг., используя расчетные данные темы 4:

Год
Годовой темп роста (снижения), %	100,0	74,8	118,1	112,2	128,9

Для удобства вычислений переведем годовые темпы роста (снижения) из процентов в единицы и подставим в формулу, получим:

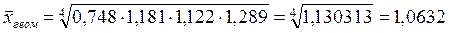
или в процентах – 106,3%.

Использование вычислительной техники и соответствующего программного обеспечения, в составе которого всегда есть необходимые функции, вычисляющие любые типы средних, позволяют в практической деятельности упростить такие расчеты.

Структурные средние

Перечисленные выше средние часто называют степенными средними. Наряду с ними существуют так называемые структурные средние. В ряде случаев с их помощью можно определить среднюю величину без про­изводства вычислений, как бы ви­зу­аль­но. Для этого используют такие средние величины, как мода и медиана.

Модой в статистике называется значение признака (варианта), котороечащевсего встречается в данной совокупности. Мода обознача­етсясимволом Мо. К этой средней прибегают для выявления величины признака, име­ющей наибольшее распространение (цена на рынке, по которой было совершено наибольшее число продаж данного товара, но­мер обуви, который пользуется наибольшим спросом у покупате­лей, и т.д.). Мода чаще всего используется в совокупностях боль­шой численно­сти.

Медианой в статистике называется варианта, которая нахо­дится в середине ранжированного (т.е. упорядоченного) ряда. Медиана делит такой ряд пополам. По обе стороны от нее находится одина­ковое число единиц совокупности. Медиана обычно обознача­ется символом Ме.

Упрощенным условным примером на­хождения моды и медианы может служить ранжированный вариационный ряд осужден­ных по возрасту (14–26 лет):

Возраст

Число осуж­ден­ных

Ме

Мо

Медианой в этом дискретном ряду будет варианта «20» с часто­той 150. По обе стороны от нее находится равное число единиц совокуп­ности. Модой в этом ряду являет­ся варианта «22» с наибольшей частотой — 175 осужден­ных.

Дата добавления: 2014-12-27