Часть 2 3 страница

Если всем единицам любого ранжированного ряда придать порядко­вые номера, то номер медианы в ряду с нечетным чис­лом членов n определяется как (n +1)/2. В случае, если число членов в ряду четное, то медианой будет средняя из двух центральных вари­ант, порядковые номера которых n /2 и n /(2 + 1). Например, если в ряду 20 единиц, то в центре стоят единицы с порядковым номе­ром 10 и 11. Средняя из двух величин определяется по формуле средней арифметической. В подобных случаях в качестве медианы можно определить и одну варианту, если единиц в совокупности много и различия между ними незначительные.

3 Показатели вариации признака

Средние величины раскрывают важную обобщающую харак­тери­стику совокупности по варьирующему признаку. Рассчитав их, необходимо уяснить, насколько они показательны, типич­ны или однородны. Для этого следует рассчитать показатель вариации (разброса значений).

Наиболее простой показатель вариации — это раз­мах вариации R. Он исчисляется в виде разности между наиболь­шими и наименьшими значениями варьирующего признака:

R=X_max - X_min

Более широко применяется следующий показатель вариации — дисперсия. Она обозначается символом s ² (сигма малая в квадра­те) и вычисляется по формуле:

где х_i – i –тое значение признака (варианты), (i = 1,…, n);

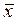– средняя арифметическая;

n – число значений признака.

При наличии повторяющихся значений можно использовать формулу для взвешенной дисперсии:

.

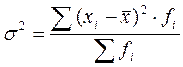Корень квадратный из дисперсии s (сигма малая) называют средним квадратическим отклонением. Дисперсия и среднее квадратическое отклонение являются наи­более распространенными показателями вариа­ции признака.

Достаточно часто используется такой показатель вариации как коэффици­ент вариации. В отличие от размаха вариации, среднего квадратического отклонения и дисперсии, ко­торые выражаются в абсолютных и именованных числах, ко­эффициент вариации является показателем относительным. Он выражается в долях или процентах, обозначается символом V и рассчи­тывается по формуле:

где s – среднее квадратическое отклонение;

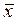- средняя арифметическая.

Коэффициент вариации предоставляет большие возможности для сравнительных изучений, поскольку сравнивать, например, средние квад­ратические отклонения вари­а­ционных рядов с разны­ми уровнями непос­редственно нельзя. Коэффициент ва­ри­а­ции в известной мере является кри­терием типичности средней. Если он относительно боль­шой (например, выше 40%), то это значит, что типичность такой средней очень невысока. И наоборот, если его значение малое, то средняя является типической и надежной.

Перечисленные выше показатели вариации признаков вычисляются, как правило, с помощью соответствующих функций, включенных в прог­рам­мное обеспечение, применяемое для статистического анализа.

Вопросы для самопроверки

1) Укажите главное условие, которое необходимо выполнить при расчете средней величины.

2) Как рассчитать среднюю арифметическую?

3) Для расчета какого показателя динамики применяется средняя геометрическая?

4) Как определить такую структурную среднюю величину как мода?

5) Какую структурную среднюю в статистике называют медианой?

6) Что характеризуют показатели вариации?

7) Какие показатели вариации наиболее часто применяют в статистике?

Тема 7. ВЫБОРОЧНЫЙ МЕТОД СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ

1 Понятие выборочного наблюдения

Основной формой сбора криминологической и социально-правовой информации являет­ся статистическая отчетность правоохранительных и других юри­дических учреждений. Но их отчеты, отражая важнейшие показа­тели, ограничены по объему. Поэтому по актуальным вопросам, которые не отра­жены в официальной отчетности, следует проводить специально организованные изучения, применяя такое несплошное наблю­дение, которое дает относительно надежные и достоверные дан­ные. Это достигается при выборочном наблюдении. Оно позволя­ет с большей надежностью, чем другие способы несплошного наблюдения, проводить изучение, задавать и рассчитывать необ­ходимые пределы точности и вводить соответствующие поправки в полученные результаты.

Методика выборочного наблюдения досконально разработа­на математической статистикой. Оно получило самое широкое при­знание и распространение в различных отраслях науки и практи­ки как метод, во многих случаях замещающий сплошное изуче­ние тех или иных явлений и процессов.

Под выборочным понимается метод статистического исследо­вания, при котором обобщающие показатели изучаемой совокуп­ности устанавли­ваются по некоторой ее части на основе положений случайного отбора.

При выборочном методе обследованию под­вергается сравнительно небольшая часть всей изучаемой сово­купности (обычно до 5 — 10%, реже до 15 — 25%). При этом под­лежащая изучению совокупность, из которой про­изводится отбор части единиц, называется генеральной совокупно­стью, а ее показатели называются генеральными (генеральная средняя, генеральная дисперсия). Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью, или просто выборкой и ее показатели называются выборочными.

В основе отбора единиц для обследования положены принципы рав­ных возможностей попадания в выборку каждой единицы гене­ральной совокупности. Именно в результате соблюдения этих прин­ципов исключа­ется образование выборочной совокупности только за счет лучших или худших образцов.

Свойство выборки воспроизводить с требуемой точностью характе­ристики генеральной совокупности называется репрезентативностью.

Если выборка репрезентативна, то, рассчитав по определенным формулам характеристики выборочной совокупности, эти характеристики можно приписать с той или иной степенью достоверности всей генераль­ной совокупности.

Поскольку изучаемая статистическая совокупность состоит из единиц с варьирующими признаками, то состав выборочной сово­купности может в той или иной мере отличаться от состава гене­ральной совокупности. Это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности со­ставляет ошибку выборки. Она зависит от ряда факторов: степени вариаций изучаемого признака, численности выборки, методов от­бора единиц в выборочную совокупность, принятого уровня досто­верности результата исследования.

Ошибки бывают тенденциозными (систематическими) и случайными. Первые – результат неправильного или преднаме­ренного отбора исследо­вателем тех или иных показателей, вто­рые – результат случайностей неполного отбора.

Тенденциозные ошибки возникают тогда, когда исследователь неправильно сфор­мировал выборку, не выполнил правила отбора единиц совокупности, сознатель­но отобрал наиболее по­казательные единицы. Например, исследуя пра­во­соз­на­ние граж­дан, анкетёр в целях экономии времени воспользовался аудито­рией студентов-юристов и опросил их. Полученные данные, ес­тественно, отражали пра­во­вые взгляды лишь этих респондентов и не соответствовали взглядам всех граждан. Вы­воды, сделанные на основе тенденциозных выборок, будут ошибочными.

Истории известны многие курьезы, связанные с пренебреже­нием правилами выбороч­ного наблюдения. Один из них произо­шел в США в 1936 г. при прогнозировании исхода президентских выборов. Журнал «Литерари Дайджест», используя телефонные книги, опросил свыше 2 млн человек. По итогам опроса президентом должен быть избран Ландон. Социологи Геллап и другие опросили только 4 тыс. жителей и пришли к однозначному выво­ду: победит Рузвельт. Их прогноз оправдался. В чем причина таких расхождений? Первая выборка отражала мнение лишь состоятель­ных кон­сер­ва­тив­ных слоев населения, которые имели телефоны, вторая — всех слоев населения. Она оказалась более представи­тельной, хотя была в 500 раз меньше первой. Роковую роль сыг­рали тенденциозные ошибки.

Тенденциозных ошибок можно избежать, но нельзя оценить их величину; случайные ошибки избежать нельзя, но можно рассчитать.

При использовании выборочного метода обычно используют два основных вида средних обобщающих показателей: относительную долю (удельный вес) альтернативного признака и среднюю величину количест­венного признака.

Атрибутивный признак «переводится» в альтернативный таким образом, что колеблемость качественного признака становится двухвари­антной: совершено преступление против собственности или иное, в состоянии опья­нения правонарушителя или трез­вым субъектом, по мотиву мес­ти или иным побуждениям, лицом, воспитанным в не­пол­ной или полной семье, интровертом или экстравертом и т. д.

Дисперсия альтернативного признака рассчитывается по формуле:

.

Следует отличать два различных способа формирования выборки: повторный и бесповторный. В первом случае любая из единиц генераль­ной совокупности может попасть в выборку не один раз, во втором случае возможность повторного попадания любой единицы совокупности полностью исключена.

Математическая статистика дает формулы для расчета ошибки, вызванной случайностью отбора единиц совокупности в выборку. Для повторной выборки формула имеет вид:

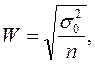
где W – ошибка выборки;

σ₀² – дисперсия генеральной совокупности;

n – объем выборки (число единиц совокупности в выборке).

Чаще всего характеристики генеральной совокупности (в том числе и дисперсия) неизвестны, поэтому в формулу подставляют значение выборочной дисперсии, которое при малом объеме выборки (n < 30) рассчитывается следующим образом:

где σ ² – дисперсия, вычисляемая по ранее приведенной в теме 6 формуле.

Очевидно, что по мере роста объема выборки n значения выборочной дисперсии приближаются к дисперсии генеральной совокупности.

Анализ формулы для расчета ошибки выборки показывает, что чем меньше разброс признака, который характеризуется дисперсией, и чем больше объем выборки, тем меньше ошибка.

При использовании бесповторного отбора единиц совокупности в выборку формула для расчета ошибки выборки имеет вид:

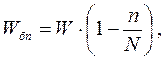
где W_бп – ошибка бесповторной выборки;

W – ошибка повторной выборки;

N – объем генеральной совокупности.

В случаях, когда объем генеральной совокупности неизвестен, сомножи­тель в круглых скобках не учитываются, что приводит к некоторому завышению ошибки выборки.

Итак, после правильно организованного выборочного наблюдения несложно произвести вычисления среднего арифметического значения количественного признака или выборочной доли альтернативного признака, а также соответствующей дисперсии, ошибки выборки. Полученные таким образом характеристики доли и средней в генеральной совокупности отличаются от показателей выборочной совокупности на величины ошибки выборки W.

Но такое суждение справедливо не с абсолютной достоверностью, а с определенной степенью вероятности.

В математической статистике доказывается, что вероятность отклонения изучаемого признака генеральной совокупности, как качествен­ного, так и количественного, в пределах однократной ошибки выборки от показателей выборочной совокупности равна 0,683; в пределах двукрат­ной ошибки – 0,954; в пределах трехкратной ошибки – 0,997.

Вероятность, принимаемая при расчете ошибки выборки, называется доверительной. Между доверительной вероятностью и кратностью ошибки, которую называют коэффициентом доверия, есть функциональ­ная связь. Ее установил известный русский математик А.М.Ляпунов (1857-1918) и на практике пользуются таблицами, в которых приведены значения доверительной вероятности для различных значений коэффициента доверия, обозначаемого t.

При криминологических, социально-правовых ис­следованиях и при изучении в практических оперативных целях может быть допустима точность с коэффициентом доверия t = 1. При ре­шении важных научных или практических вопросов желательно, чтобы ошибка репрезентативно­сти принималась с коэффициентом доверия t = 2. Изучение с коэффици­ентом доверия t = 3 в юридичес­кой статистике практически нигде не требуется.

Что такое доверительная вероятность 0,683? Это означает, что в 683 случаях из 1000 генеральная доля и генеральная средняя могут находиться в пределах одно­кратной ошибки выборки, а в остальных 317 случаях могут выйти за ее пре­делы.

Введем понятие доверительной (предельной) ошибки выборки как произведение ошибки выборки на соответствующий коэффициент доверия:

D = W×t.

Предельная ошибка выборки обозначается греческой буквой D (дельта). После ее расчета легко оценить показатель генеральной совокупности. Для количественного признака рассчитываем пределы, в которых находится значение генеральной средней:

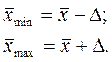
Для альтернативного признака рассчитываем пределы, в которых находится значение относительной доли (удельного веса) этого признака в генеральной совокупности:

В качестве примера применения выборочного метода исследования для количественного признака оценим средний возраст осужденных, если случайная бесповторная выборка из 2000 статкарточек дала следующие данные:

Возрастной интервал	20 - 25	25 – 30	30 - 35	35 - 40	40 - 45	45 - 50
Среднее значение
Число осу­жденных

1. Рассчитаем выборочные характеристики – среднюю арифметиче­скую и дисперсию. Обычно эти расчеты проводят с использованием программных средств на компьютере, но возможен и ручной расчет:

,

.

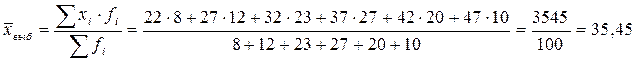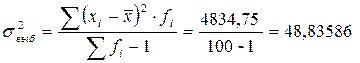2. Определим ошибку выборки при использовании бесповторного отбора единиц совокупности:

3. Задаемся доверительной вероятностью, а, следовательно, и величи­ной коэффициента доверия. Так как имеем дело с обычным исследо­ванием, то расчет выполним для доверительной вероятности 0,683 (t = 1).

4. Рассчитаем доверительную ошибку: D = W_бп×t =0,66389.

5. Определим пределы, в которых лежит средний возраст осужденных в генеральной совокупности:

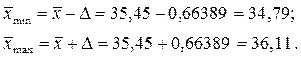
Таким образом, с вероятностью 0,683 средний возраст осужденных лежит в пределах от 34,8 до 36,1 лет.

2 Виды отбора единиц выборочной совокупности

Достоверность выборочных показателей существенно зависит от строгого соблюдения правил случайного от­бора единиц совокупности. Понятие «случайный отбор» нельзя понимать в обыденном значении слова: все, что случайно попадет в поле зрения исследователя, то и изучается. Случай­ность — здесь не синоним беспорядочности. Ибо и при беспоря­дочном отборе единиц совокупности может проявиться та или иная тенденциозность.

Случайный способ выборки предполагает строгую процедуру ее организации и проведения. Термин «случайный» здесь упо­требляется как антоним тенденциозной выборки. Случайная вы­борка порождает случайные ошибки, которые имеют закономер­ности распределения. Они измеряются и вычисляются. В этих слу­чаях исследователь точно может сказать, какова достоверность результатов проведенного изучения. Для обеспечения независи­мости изучения от субъективных желаний исследо­вателя, отбор единиц совокупности следует производить так, чтобы каждая еди­ница исследуемой генеральной совокупности имела одинако­вые шан­сы попасть в выборку наравне со всеми другими единицами данной совокупности. Принцип равновозможности и случайности при отборе единиц в выборку осуществляется следующими способа­ми: собст­венно случайным, механическим, типическим и райо­нированным. Каждый из них может быть повторным и бесповтор­ным.

Собственно случайный отбор дают лотерея, жеребь­евка, использование таблиц или генераторов случайных чисел. Напри­мер, для прове­дения выборочного анкетного опроса граждан бе­рется список избирателей или иной пронумерованный список граждан. Все номера списка записыва­ются на листках бумаги и всле­пую вынимается столько листков, сколько единиц совокупности должна содержать вы­борочная совокупность. Опрашиваются лишь те граждане, номе­ра фамилий которых определены жребием.

Собственно случай­ный отбор может быть применен при выборке статкарт на выяв­лен­ное преступление, на лицо, совершившее преступление, на осужденного и т.д., когда из генерального массива тщательно перемешанных перфокарт вслепую вынимается столько карт, сколько необходимо для выборочной совокупности. В приведен­ных примерах собственно случайной выборки можно применить как бесповторный отбор, когда вынутая фишка или перфокарта не возвращаются в массив, так и повторный, когда вынутые еди­ницы после изучения возвращаются обратно в массив.

Механический отбор — разновидность случайного. При механическом отборе генеральная совокуп­ность делится на столько равных частей, какова должна быть выборка, а потом из каждой части обследуется одна едини­ца. Например, в генераль­ной совокупности насчитывается 5000 статкарт. Выборочная совокупность определяется равной 250 единицам, т. е. 5% от генеральной. В этом случае 5000: 250 = 20. Из тщательно перемешанного массива статкарт отбирается каж­дая двадцатая и обследуется. При 10%-ной выборке отбирается и обследуется каждая десятая карта, при 20%-ной — каждая пятая и т. д. Механическая выборка, как прави­ло, бывает бесповторной.

Типический отбор обычно сочетается с собственно случай­ной или механической выборкой. Он призван для того, чтобы при изучении совокупности отражалась вся ее сложная струк­тура. Дело в том, что собственно случайный или механический отборы непосредственно приме­нимы лишь при изучении од­нородной совокупности по какому-то одному признаку. Юри­дические изучения обычно проводятся по ряду признаков. В этом случае выборка, имеющая достаточный объем для одного при­знака, может оказаться недостаточной для другого, пятого, десятого. А надо, чтобы выборка репрезентировала каждый из изучаемых признаков, а точнее — всю сложную структуру ге­неральной совокупности. Это относится к любому элементу предмета изучения. Все они являются сложными по своей струк­туре. Преступность, например, подразделяется по видам, мо­тивации, тяжести и т. д. При изучении ее в выборку могут по­пасть в большей мере признаки преступлений против личнос­ти, в меньшей — против собственности и совсем не попасть неосторожные деяния. А выборочная совокупность должна быть копией генеральной, ее уменьшен­ной моделью. Это достижи­мо при типической выборке. При ее организа­ции вся генераль­ная совокупность предварительно подразделяется на качествен­но однородные по существенному признаку группы, а затем из них производится случайный отбор. В нашем примере статкарты на преступления вначале распределяются по видам деяний, а затем из каждого подмассива отбирается необходимое коли­чество статистических карт случайным или механическим спо­собом. Типическую выборку иногда называют расслоенной, или стратифицированной.

Типический отбор может сочетаться с несколькими стадиями (ступе­нями) отбора. На первой стадии, например, отбираются статкарты по виду криминальной мотивации. Здесь единица от­бора — это мотивация (корыстная, насильственная и т. д.). Затем внутри каждой мотивации отбираются по родовому объекту по­сягательства. На третьей стадии внутри каждого родового объекта отбираются карты по видам деяний. Могут быть и последующие ступени. Такая выборка именуется многосту­пенчатой. Распреде­ление объектов изучения по территориям может потребовать рай­онированной многоступенчатой выборки. В конкретных исследованиях возможно комбинированное сочетание различных видов отбора.

Выборочное наблюдение получило самое широкое распрост­ранение в мире. Освоение его методик лицами, занимающимися изучением и анализом криминологических, деликтологических, социально-правовых и других массовых общественных явлений и процессов, с чем связана любая юридическая деятельность, жиз­ненно необходимо. Грамотное применение этих методик помога­ет получить надежные данные, отсутст­вующие в официальной отчетности, за короткое время с использованием малых сил и средств.

Вопросы для самопроверки

1) Сформулируйте сущность выборочного метода статистического исследования.

2) Какое свойство выборки называют репрезентативностью?

3) Какими обстоятельствами определяется случайная ошибка выборки? Тенденциозная ошибка?

4) Как зависит случайная ошибка выборки от объема выборки?

5) Каким образом при проведении выборочного исследования можно перейти от атрибутивного признака к альтернативному?

6) Какие способы отбора единиц совокупности применяют при реализации выборочного метода?

Тема 8. ДИНАМИЧЕСКИЕ РЯДЫ

1 Понятие о динамических (временных) рядах и их виды

В судах, органах прокуратуры, внутренних дел, налоговой полиции, таможенной служ­бы, адвокатуре, нотариате и дру­гих юриди­чес­ких учреж­дениях ведется многолетний непрерывный государственный и ведом­ст­вен­ный учет преступности, судимости, административной правонарушае­мости, граж­дан­ско-правовых споров, рождений, браков, смертей и других юридически значимых яв­ле­ний. Это дает возможность по накопленным в течение десятков лет дан­ным выявлять и отслеживать во вре­мени проис­ходящие изменения многих тысяч различных статис­ти­чес­ких показателей. Ежедневный, ежемесячный и ежегодный сбор огромного ста­тис­ти­чес­кого материала был бы абсолютно неоправданным, если его всесторонне не анали­зи­ровать по «вертикали» (струк­тура, состояние, взаимосвязи) и по «горизонтали» (тен­ден­­ции, динамика, сезонность), «назад» (ретроспек­тива, интер­поляция) и «вперед» (эк­с­­траполяция, прогноз). Анализ дина­мики юридически значимых явлений за длительный пе­ри­од времени дает возможность понять их развитие в прошлом, на­стоящем и воз­мож­ном будущем, оценить эффективность дея­тельности юридических учреждений и спланировать ее на пер­спективу.

Основная тенденция в изменении явлений во времени в ста­тисти­ческой литературе называется трендом. Характер тренда изучаемого яв­ле­ния иногда очеви­ден при первом ознакомлении с динамическими рядами абсо­лютных пока­зателей. Но чаще всего тенденции и закономер­ности развития явления прояв­ля­ют­ся в процессе различных преобразо­ва­ний рядов динамики с использованием отно­си­тель­ных и сред­них величин.

Ряды динамики или временные ряды - это число­вые значения конкретного статистического показателя за определенный промежу­ток времени (месяц, квартал, год, пятилетие и т. д.). В ряду динамики имеется два основных показателя: пока­затель времени (шкала времени) и уровень ряда (шкала уровня ряда). Уровень ряда обычно выражен в абсолютных величинах, на основе которых в процессе аналитической работы рассчитываются обобщающие величины (относительные и средние).

Ряды динамики делятся на момен­т­ные и интер­вальные, которые в свою очередь могут иметь множество разно­вид­нос­тей: ряды темпов роста, темпов прироста, коэффициен­тов, индексов и т. д.

Моментные ряды характеризуют уровни изменения юридичес­ки значимых явлений на определенные моменты времени (дату учета), например, на начало месяца, квар­та­ла, года или по со­стоянию на 1 янва­ря, 30 июня, 31 декабря и т.д. Типичные мо­мент­ные ряды в юридиче­ской статистике - количество заклю­ченных в колониях, тюрьмах, следст­венных изоляторах или чис­ло судей, прокуроров, следователей, адвока­тов, юрис­консуль­тов в учреждениях, регионе, стране, приходящееся на какую-то дату нескольких лет. Период между датами в моментных рядах называ­ется интервалом ряда. Он может быть годовым, квартальным, ме­сячным. Особенностью моментного ряда является то, что его по­казатели, раскрывая то или иное состояние, не могут суммиро­ваться или ук­руп­няться. Число судей, числящихся по состоянию на 1 января 2002 г., нельзя сум­ми­ро­вать с числом судей, числя­щихся на 1 июля, т. е. на начало второго полугодия дан­ного года, или на 1 января 2003 г., поскольку это могут быть одни и те же штатные еди­ницы, если даже общее число судей как-то измени­лось (некоторые судьи уволились или перешли на другую рабо­ту, а на их место или на вновь открывшиеся вакансии пришли новые).

Интервальные ряды характеризуют величину изучаемого пока­за­теля, полученного за какой-то период времени (интервал). Если в момент­ном ряду интервал — промежуток времени между датами учета сведений, то в интервальном ряду интервал — тот же про­межуток времени, но за который обобщены приводимые сведения, когда они накап­ли­ва­лись. Поэтому месячные данные можно суммиро­вать по кварталам, кварталь­ные — по годам, годовые — по пяти­летиям и т. д. В моментном ряду величина уровня ряда не зависит от размера интервала. И на начало каждого месяца, и на начало каждого года общее число сотрудников прокуратуры в городе N может быть одним и тем же. В ин­тер­вальном ряду величина уровня ряда существенно зависит от размера интервала. Число учтенных преступлений за год может быть (примерно) в 12 раз больше, чем за любой из его месяцев. Иногда говорят, что моментный ряд учи­ты­вает состояние на какой-то момент, а интервальный ряд отра­жает деятельность (совершение прес­туп­ле­ний, борьба с преступ­ностью, установление юридических фактов и т. д.), сведения о ко­торой характери­зуются накопительностью.

На основе рядов динамики абсолютных величин в момент­ном и интервальном рядах могут быть получены ряды динамики относительных и средних величин, что дает воз­мож­ность много­кратно увеличить аналити­ческие возможности динамических ря­дов.

Основное требование, предъявляемое к анализируемым рядам динамики, — это сопоставимость их уровней по содержанию учи­тываемых явлений, отрезку времени учета, территории, полноте охвата и другим параметрам. Причин несопоставимости много. Они должны учитываться в процессе конкретного анализа. Остановимся на основных.

Изменение содержания учитываемых явлений. Это прежде всего относится к изменениям понятия преступного, противоправного и других юридических дефиниций. В УК РСФСР за все время его действия было внесено более 700 изменений и допол­не­ний. Осо­бенная часть была дополнена 120 новыми статьями (со значка­ми), кримина­ли­зи­рующих действия, которые ранее не считались преступными или считались, но не в том объеме. Наряду с этим из нее было исключено около 40 статей, то есть декри­ми­на­ли­зировано около 40 деяний. УК РФ кримина­лизировал около 70 но­вых деяний и де­кри­ми­нализировал или как-то транс­формировал 78 составов преступлений, которые зна­чи­лись в прежнем УК. Еще более изменчива правовая картина в административ­ной юрисдик­ции. Аналогичные изменения происходили в связи с приня­тием соот­ветс­тву­ю­щих частей ГК РФ, Семейного, Лесного и других кодексов и федеральных законов. Нормативные изменения такого плана оказывают существенное влияние на сопос­та­ви­мость юри­диче­ски значимых показателей.

Изменение территории, к которой отнесены те или иные показатели. Коренные изменения админи­стративно-тер­рито­ри­аль­ного деления в Российской Федерации и в СССР в целом имели место: после рево­лю­ции 1917 г.; после присоединения к СССР западных областей Украины, Белорус­сии, Молдавии и прибалтийских республик в 30—40-е гг. с об­щей численностью населения более 20 млн. человек; при времен­ной потере западных областей в период Великой Отечественной войны 1941-1945 гг.; при передаче Крымской области из РСФСР в Ук­ра­инскую ССР в 50-е гг.; после упразднения администра­тивно-территориальных образо­ва­ний при депортации немцев, кал­мыков, чеченцев, ингушей и других народов в 40-е гг. и при вос­создании большинства из этих образований после реабилитации депор­ти­ро­ванных народов; после распада СССР в 1991 г.; при образовании 89 субъектов Фе­де­рации на территории Российской Федерации в 90-е гг. и т. д. Мно­гие территори­альные изменения происходили внутри субъек­тов Федерации.

Изменение учета преступлений, судимости, административ­ных правона­рушений, гражданско-правовых деликтов может ока­зать суще­ственное влияние на сопос­та­ви­мость рядов динамики. Все показатели динамического ряда должны быть выражены в одинаковых единицах измерения и быть однотипными по мето­дике вычисления. Пос­ле приня­тия Правил единого учета преступлений в 1965 г. этот учет неодно­кратно из­ме­нялся и дополнялся. Трижды меня­лась только общая редакция Инструкции учета (1985, 1994, 1997 г.). Серьезные изменения происходили в учете тяжких преступлений, посколь­ку их перечень неоднократно существенно менялся. Большие из­менения происходили в учете заключенных.

Дата добавления: 2014-12-27