Виды колебаний

§ Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

§ Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (т.е. чтобы зависимость от времени этой силы была синусоидальной).

• Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника меняет свое положение координата его центра масс, при переменном токе меняют свои характеристики с определенной повторяемостью напряжение и ток в цепи. Колебательный процесс может имет различную физическую природу, поэтому различают колебания механические, электромагнитные и др. Но различные колебательные процессы характеризуются одинаковыми физическими параметрами и одинаковыми уравнениями. Отсюда вытекает целесообразность единого подхода к исследованию колебаний различной физической природы. Например, единый подход к исследованию механических и электромагнитных колебаний использовался английским физиком Д.У.Рэлеем (1842—1919), русским инженером-экспериментатором П. Н. Лебедевым (1866—1912), А.Г.Столетовым. Большой вклад в развитие теории колебаний сделали Л. И. Мандельштам (1879—1944) и его ученики.
  
  Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
  
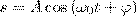  (1)
  
  где ω₀ — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω₀t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.
  
  Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
  
  
  
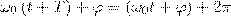
  откуда
  
  (2)
  
  Величина, обратная периоду колебаний,
  
  (3)
  
  т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
  
  
  
  Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
  
  Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
  
  (4)
  
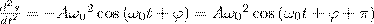  (5)
  
  т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω₀ и Аω₀². Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d²s/dt² равен наибольшему положительному значению (рис. 1).
  
  
  
• 
• 
  
  
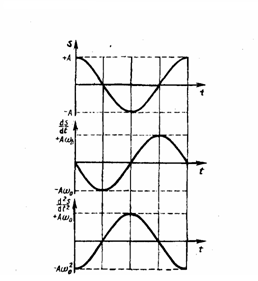
• Рис.1

§

Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний

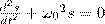(6)

(где s = A cos(ω₀t+φ)). Решением данного дифференциального уравнения является выражение (1).

36. Волны. Уравнение бегущей волны. Волновое уравнение.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры^[1]».

В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO₃), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся^[2]. Одним из часто встречающихся признаков волн считаетсяблизкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и она^[2].

Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов^[2]. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений^[2]. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.

По своему характеру волны подразделяются на^{[ источник не указан 97 дней ]}:

§ По признаку распространения в пространстве: стоячие, бегущие.

§ По характеру волны: колебательные, уединённые (солитоны).

§ По типу волн: поперечные, продольные, смешанного типа.

§ По законам, описывающим волновой процесс: линейные, нелинейные.

§ По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.

§ По геометрии: сферические (пространственные), одномерные (плоские), спиральные.

Отличие колебания от волны.

Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»^{[ источник не указан 97 дней ]}).

В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.

Уравнение плоской одномерной синусоидальной волны:

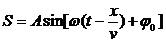
(Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, j₀ - начальная фаза колебаний в точке х = 0, w - частота (циклическая) волны.

Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ l = nT.

ВОЛНОВОЕ ЧИСЛО k:

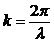
С помощью введенного волнового числа уравнение волны запишется:

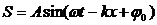
Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:

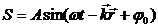
здесь r - радиус вектор точки пространства; j₀ - начальная фаза колебаний в начале координат.

Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:

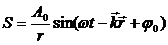
A ₀ = const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.

Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:

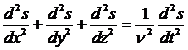или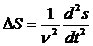

Здесь D S - оператор

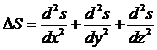
Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:

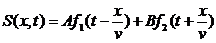
Здесь А и В - произвольные константы, а f₁ и f₂ - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.

37. Интерференция и дифракция волн.

38. Звуковые и электромагнитные волны.

Звуковые волны.

Звук – колебательное движение частиц упругой среды, распространяющееся в виде волн (колебания плотности, давления). Не может распространяться в вакууме! Продольная волна в жидкостях и газах!

Инфразвуки (до 16 Гц)

Слышимые звуки (16 – 20000Гц)

Ультразвуки (более 20000 Гц)

Гиперзвуки (10⁹ – 10¹³ Гц)

Источники

Шум атмосферы, леса, моря. Гром. Взрывы, орудийные выстрелы. Сейсмические волны.

Колебания твердого тела (мембраны, деки, диффузоры громкоговорителей). Колебания ограниченных объемов среды (воздух в музыкальных духовых инструментах, органах, свистках). Голосовой аппарат человека и животных.

Пьезоэлектрические материалы. Магнитострикционные материалы. Некоторые животные (дельфины, летучие мыши и др.).

Тепловое движение атомов. Пьезоэлектрические и магнитострикционные материалы.

Применение

Определение места взрыва, выстрела. Предсказание цунами. Исследование атмосферы.

Ориентация в пространстве. Общение, речь, получение информации.

Дефектоскопия, медицина, эхолокация. Физика твердого тела. Получение эмульсий. Ускорение диффузии, некоторых химических реакций. Ориентация в пространстве у некоторых животных.

Изучение состояния вещества. Линии задержки (цветное телевидение, ЭВМ и т.п.)

Диапазоны слышимых звуков
Дети	20 лет	35 лет	50 лет
16 – 22000 Гц	16 – 20000 Гц	25 – 15000 Гц	30 – 12000 Гц

Скорость звука зависит от среды и ее состояния, как и для любой механической волны. Скорость звука при 0⁰С в воздухе 331,5 м/с, в воде – 1430 м/с, в стали – 5000 м/с.

Приемники звука.

1. Естественные: ухо. Обладает высокой чувствительностью (Dp=10^-6 Па) и избирательностью (например, дирижер улавливает звуки отдельных инструментов оркестра).

2. Искусственные: микрофон. Основная характеристика – чувствительность 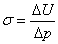(зависит от частоты звука).  

Характеристики звука.

1. Спектр – разложение на гармонические колебания по частотам.Восприятие звука органами слуха зависит от того, какие частоты входят в состав звуковой волны. Шум - звуки, образующие набор частот, непрерывно заполняющих некоторый интервал (сплошной спектр частот). Музыкальные (тональные) звуки – звуки, образующие линейчатый спектр частот: ча­стотыN входящие в состав музыкальных звуков, образуют ряд дискретных значений. Музыкальным звукам соответствуют периодические или почти пе­риодические колебания. Каждая синусоидальная звуковая волна называется тоном.

Высота тона зависит от частоты: чем больше частота, тем выше тон. Основным тоном сложного музыкального звука называется тон, соответ­ствующий наименьшей частоте, которая имеется в наборе частот данного звука. Тоны, соответствующие остальным частотам в составе звука, называются оберто­нами. Если частоты обертонов кратны частоте основного тона, то обертоны на­зываются гармоническими, причем основной тон с частотой N₀ называется первой гармоникой, обертон со следующей частотой 2N₀ - второй гармоникой и т. д.

Музыкальные звуки с одним и тем же основным тоном различаются тембром, который определяется наличием обертонов - их частотами и амплитудами, характером нарастания амплитуд в начале звучания и их спадом в конце звучания.

2. Звуковое давление – давление, оказываемое звуковой волной на препятствие.

3 .Интенсивность звуковой волны – энергия, переносимая звуковой волной через единицу поверхности за единицу времени ( ).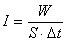    

4. Громкость звука зависит от интенсивности звука, т. е. определяется ампли­тудой колебаний в звуковой волне. Наибольшей чувствительностью ор­ганы слуха обладают к звукам с частотами от 700 до 6000 Гц. В этом диапазоне ухо способно воспринимать звуки с интенсивностью около10^-12-10^-11 Вт/м². Порогом слышимости называется наименьшая интенсивность звуковой волны, которая может быть воспринята органами слуха. Стандартный порог слышимости принимается равным I₀=10^-12 Вт/м² при частоте n=1 кГц. Порогом болевого ощущения называется наибольшая интен­сивность звуковой волны, при которой восприятие звука не вызывает болевого ощущения. Порог болевого ощущения зависит от частоты звука (на частоте 1 кГц равен 1 Вт/м²). Мерой чувствительности органов слуха к восприятию звуковых волн дан­ной интенсивности является уровень интенсивности (громкости): 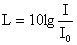. Единица измерения - децибел

Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния)электромагнитного поля (то есть, взаимодействующих друг с другом электрического и магнитного полей).

Среди электромагнитных полей вообще, порожденных электрическими зарядами и их движением, принято относить собственно к излучению ту часть переменных электромагнитных полей, которая способна распространяться наиболее далеко от своих источников — движущихся зарядов, затухая наиболее медленно с расстоянием.

Электромагнитное излучение подразделяется на

§ радиоволны (начиная со сверхдлинных),

§ инфракрасное излучение,

§ видимый свет,

§ ультрафиолетовое излучение,

§ рентгеновское излучение и жесткое (гамма-)излучение (см. ниже, см. также рисунок).

Электромагнитное излучение способно распространяться в вакууме (пространстве, свободном от вещества), но в ряде случаев достаточно хорошо распространяется и в пространстве, заполненном веществом (несколько изменяя при этом свое поведение).

39. Волновые свойства света.

Дата добавления: 2015-04-24