Равен произведению массы МТ на расстояние до оси вращения

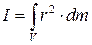
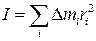Момент инерции твердого тела - Момент инерции тела относительно данной оси – это величина, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси.

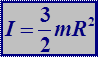Момент инерции однородного диска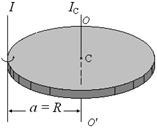

Теорема Штэйнера Момент инерции относительно произвольной оси вращения равен сумме момента инерции тела относительно параллельной оси вращения, проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями.

Для любого тела существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями. Они называются главными осями инерции.

Ось вращения, положение которой в пространстве остается неизменным в отсутствие внешних сил, называется свободной осью тела.

ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

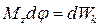Тангенциальная сила, совершая работу dA = M_zdφ увеличивает кинетическую энергию вращающегося тела на dWк.

произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.

12. Момент силы относительно точки и оси. Момент пары сил. Основной закон динамики вращательного движения.

Момент силы, вычисленный относительно точки, характеризует способность силы вызывать поворот вокруг этой точки.

Направление вектора момента силы находим по правилу правого винта.

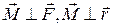Этот вектор перпендикулярен и силе, и радиус-вектору.

Момент силы относительно оси оси z – это скалярная величина, равная проекции на ось z вектора, найденного относительно произвольной точки этой оси.:

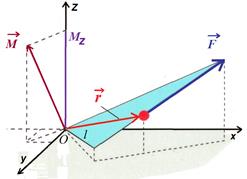
Момент пары сил:

Пара сил - две равные по величине, противоположные по направлению силы, не лежащие на одной прямой.

l - плечо пары

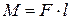
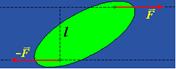
ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

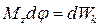Тангенциальная сила, совершая работу dA = M_zdφ увеличивает кинетическую энергию вращающегося тела на dWк.

произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.

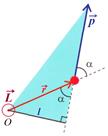
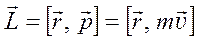13.Момент импульса. Закон сохранения момента импульса. Основной закон динамики вращательного движения.

Для материальной точки отн. точки О:

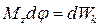
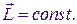
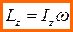
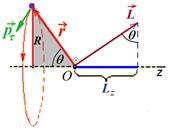Момент импульса относительно оси вращения определяется так же, как и момент силы. Нужно найти вектор момента импульса относительно произвольной точки оси, затем взять проекцию вектора на эту ось. Момент импульса твердого тела.Направление вектора.также определяется по правилу правого винта

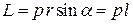
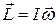Для однородного симметричного тела, вращающегося вокруг оси симметрии, справедливо векторное равенство:

Закон сохранения момента импульса В замкнутой системе тел полный момент импульса сохраняется.

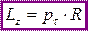ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯТангенциальная сила, совершая работу dA = M_zdφ увеличивает кинетическую энергию вращающегося тела на dWк.

произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку

14. Работа, совершаемая при вращении тела. Кинетическая энергия вращения. Сравнительный расчет скоростей центра масс шара и диска, скатывающихся с наклонной плоскости.

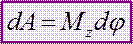
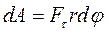
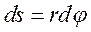
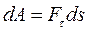
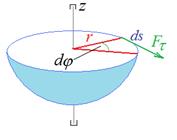Если M_z = const., то

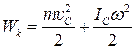
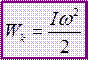
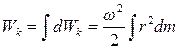
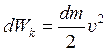
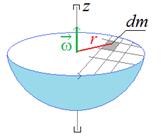Для каждой МТ:

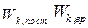15. Колебательное движение. Виды колебаний. Гармонические колебания. Их уравнение, график, характеристики. Скорость, ускорение и энергия при гармонических колебаниях.

Колебания – это процессы, повторяющиеся во времени

Свободные (собственные) колебания происходят без переменных внешних воздействий.

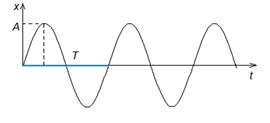
Колебания периодические,если значения изменяющихся величин повторяются через равные промежутки времени. Время одного полного колебания - это период Т.

Гармонические колебания происходят по закону синуса или косинуса.

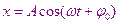Формула (кинематическое уравнение) гармонического колебания:

х – значение колеблющейся величины в момент времени t (отклонение от положения равновесия)

Характеристики гармонических колебаний:

A — амплитуда колебаний (максимальное значение колеблющейся величины);

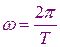циклическая частота;

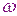
начальная фаза колебаний

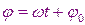Величина - это фаза колебаний. Именно она определяет значение х в данный момент времени.

Скорость и ускорение:

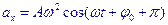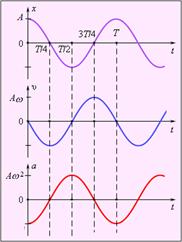
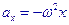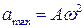Амплитуда ускорения

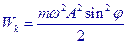Кинетическая энергия

Потенциальная энергия

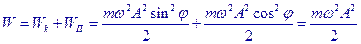Полная энергия

16.Представление и сложение однонаправленных скалярных колебаний с помощью векторной диаграммы. Сложение однонаправленных колебаний близкой частоты. Биения. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу

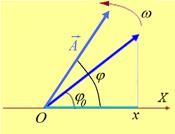
Гармонические колебания можно представить в виде проекции на ось х вращающегося вектора. Его модуль равен амплитуде колебаний. Угол с осью при t = 0 равен начальной фазе. Угловая скорость вращения равна циклической частоте. В произвольный момент времени угол равен фазе колебаний

.

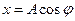Сложение колебаний

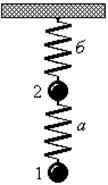
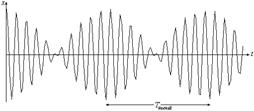
Биения -При сложении однонаправленных колебаний неравных частот один вектор “обгоняет” другой. Амплитуда результирующего колебания зависит от времени. Если частоты колебаний близки, наблюдаются биения. Это периодические изменения амплитуды результирующего колебания.

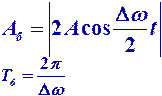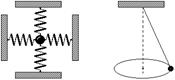
Сложение взаимно перпендикулярных колебаний

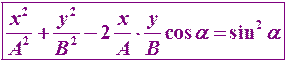При разности фаз

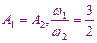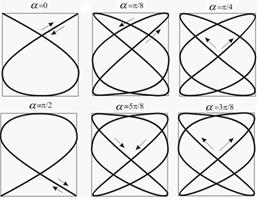
Фигуры Лиссажу для случая при различных значениях разности начальных фаз

17.Затухающие колебания. Их уравнение, график и основные характеристики.

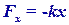Затухающие колебания- колебания, энергия которых уменьшается с течением времени.

Дата добавления: 2015-04-24