Основное уравнение МКТ

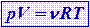
Уравнение Менделеева-Клайперона

Закон Авогадро 1 киломоль любого газа занимает при одинаковых условиях одинаковый объем.

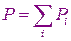Закон Дальтона Давление смеси газов равно сумме парциальных давлений

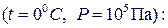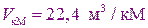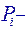парциальные давления (каждого газа в отдельности)

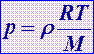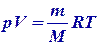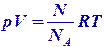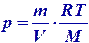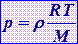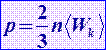2. Число степеней свободы механической системы и молекулы газа. Распределение энергии по степеням свободы. Средняя энергия многоатомной молекулы. Внутренняя энергия идеального газа.

Число степеней свободы это число независимых координат, которые необходимо задать для определения положения тела в пространстве

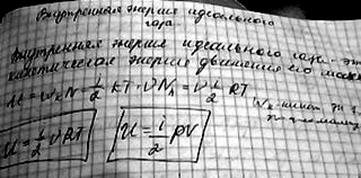
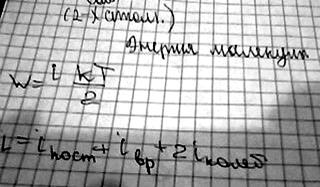
3.Распределение Максвелла скоростей и кинетических энергий молекул. Вероятностный характер законов распределения. Наиболее вероятная, среднеарифметическая и среднеквадратичная скорости молекул. Экспериментальная проверка распределения Максвелла.

Распределение Максвелла - У всех молекул разные скорости. При столкновениях эти скорости изменяются.

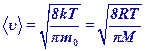
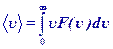
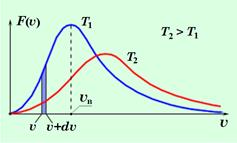
Средняя скорость молекул

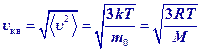Среднеквадратичная скорость молекул

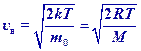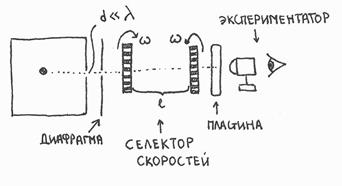
Экспериментальная проверка распределения Максвелла.

Описание опыта Штерна.

Описание опыта Ламмерта.

Описание доски Гальтона

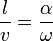На опыте (на рисунке) внутри ящика находится газ, молекулы которого вылетают через отверстие наружу. Диаметр отверстия много меньше длины свободного пробега молекул, молекул в ящике много, так что исчезновение вылетающих не меняет имеющееся распределение по скоростям внутри ящика. Колеса селектора, на поверхности которых находятся выступы, пропускающие или останавливающие летящие молекулы, вращаются с угловой скоростью 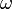. Так, преодолев первое колесо, молекула летит расстояние 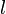до второго, которое за это время поворачивается на угол 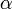. Выполняется соотношение

Так, регулируя 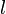, 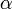и 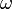, можно пропускать только молекулы с определенной скоростью 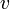. Пролетевшие через второе колесо молекулы оставляют след на пластине. Проведя эксперимент для различных значений 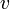, можно получить экспериментальную картину распределения скоростей в исследуемом газе. Так, с помощью этого эксперимента (в числе прочих) было подтверждено распределение Максвелла.

4. Распределение Больцмана молекул в потенциальном поле сил. Изменение концентрации молекул с высотой. Барометрическая формула.

Распределение Больцмана- В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана: P = P0exp(-mgh / kT)

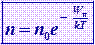
Изменение концентрации с высотой

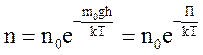
здесь n – концентрация молекул на высоте h, n₀ – то же у поверхности Земли. Так как М = m₀N_A, где m₀ – масса одной молекулы, а R = k N_A, то мы получим П = m₀gh – это потенциальная энергия одной молекулы в поле тяготения. Поскольку kT~‹ε_пост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹ε_пост›

Данное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.

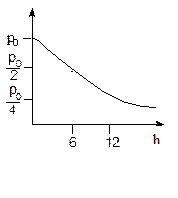Зависимость давления от высоты демонстрирует рисунок 1.3. Прибор для определения высоты над уровнем моря называется высотомером или альтиметром. Он представляет собой барометр, проградуированный в значениях высоты.

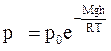5. Теплоемкость. Первое начало термодинамики и его применение для расчета отношения молярных теплоемкостей С_P/C_V.

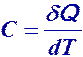Теплоемкость тела - это количество теплоты, необходимое для нагревания тела на 1 К.

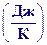Молярная теплоемкость – это количество теплоты, необходимое для нагревания одного моля вещества на 1 К.

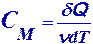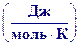Первое начало термодинамики

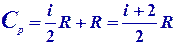
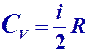Количество теплоты, сообщенное системе, идет на увеличение внутренней энергии системы и на совершение системой работы над внешними телами.

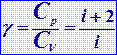Коэффициент Пуассона

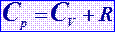Адиабатический процесс. Первое начало термодинамики для адиабатического процесса. Политропные процессы.

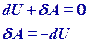
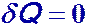Адиабатический процесс происходит без теплообмена с внешней средой.

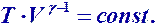
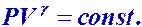Газ совершает работу за счет своей внутренней энергии. При адиабатическом расширении он охлаждается, при сжатии – нагревается.

Уравнение Пуассона для адиабатического процесса

Политропный процесс – термодинамический процесс, во время которого удельная теплоемкость (С) газа остается неизменной. Предельными частными явлениями политропного процесса являются адиабатический и изотермический процессы. В случае идеального газа изобарный и изохорный процессы также являются политропными.

Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии^[4], то адиабатический процесс в силу отсутствия теплообмена (Δ Q = 0) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид

,

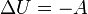где 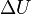— изменение внутренней энергии тела, 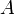— работа, совершаемая системой, 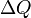— теплота, полученная системой.

Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит^[7]:

,

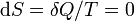где T — температура системы. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла^[7].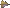

7. Работа газа при изменении объема. Расчет работы, совершаемой газом в различных изопроцессах.

Изотермический. Т.к. 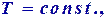то внутренняя энергия газа не изменяется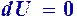

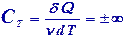
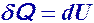
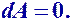Изохорный

работа моля газа при нагревании на 1 К

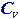
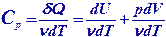
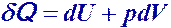Изобарный

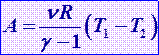Адиабатический

Работа газа при изменении объема dA=pdV

. Найдем работу газа при расширении его объема δA = Fdl = pSdl =pdV, где F – сила, с которой газ действует на поршень, dl – перемещение поршня. Если зависимость р(V) изобразить графически, то общая работа при изменении объема от V₁ доV₂ равна площади фигуры, ограниченной кривой р(V), осью абсцисс и прямыми V= V₁ и V= V₂ (рис.2.2.). Графически можно изображать лишь равновесные процессы, и все количественные выводы термодинамики строго применимы только к равновесным процессам. При достаточно медленном протекании реальные процессы можно приближенно считать равновесными. Первое начало термодинамики выполняется во всех процессах, связанных с обменом энергией и совершением работы.

8. Столкновения молекул. Эффективный диаметр молекул, средняя длина свободного пробега.

Молекулы газа сталкиваются друг с другом.

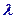Расстояние, которое молекула в среднем проходит между двумя последующими соударениями, называют средней длиной свободного пробега.

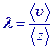Эффективный диаметр молекул – это кратчайшее расстояние, на которое они сближаются при столкновении.

Средний путь за 1 сек./ среднее число ударов за 1 сек.

9. Макро- и микросостояния. Понятие статистического веса (термодинамической вероятности). Равновесное макросостояние, флуктуации параметров состояния. Обратимые и необратимые процессы. Энтропия и ее свойства. Второе начало термодинамики. Статистический смысл энтропии. Гипотеза Приведенная теплота. Вычисление энтропии. Теорема Нернста. Вечные двигатели I-го и II-го рода.

Макросостояние – это состояние, заданное с помощью величин, характеризующих всю систему в целом (p, V, T).

Микросостояние – это состояние, заданное с помощью координат и импульсов всех молекул.

Число микросостояний соответст-вующих данному макросостоянию, называют термодинамической вероятностью или статистическим весом этого макросостояния.

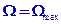Равновесному макросостоянию соответ-ствует наибольшая термодинамическая вероятность:

Система может испытывать небольшие отклонения от равновесного состояния. Их называют флуктуациями.

Обратимый процесс может происходить как в прямом, так и в обратном направлении через те же промежуточные состояния. Если система вернулась в исходное состояние, ни в ней, ни в окружающей среде не возникает никаких изменений. Обратимый процесс протекает через равновероятные состояния.

Необратимые процессы протекают только в одном направлении. Обратные им процессы маловероятны. Например, расширение газа в пустоту.

Величину S=kln называют энтропией.

Энтропия характеризует степень молекулярного беспорядка.

Упорядоченные состояния реализуются малым числом способов – энтропия мала. Неупорядоченные состояния реализуются большим числом способов – энтропия велика.

Второе начало термодинамики В изолированной системе энтропия не убывает.

Она увеличивается при необратимом процессе и остается неизменной при обратимом процессе.

Вычисление энтропии Отношение называют приведенной теплотой.

В обратимом процессе

Теорема Нернста

Следствие:

1. Любая теплоемкость системы при T стремится к 0 стремится к нулю.

2. Абсолютный нуль температуры недостижим.

Вечный двигатель первого рода – устройство, способное бесконечно совершать работу без затрат топлива и других энергетических ресурсов. По ЗСЭ его изобретение невозможно. Также невозможность его осуществления постулируется в первом начале термодинамики

Вечный двигатель второго рода – машина, которая будучи пущена в ход, превращала бы работу в тепло, извлекаемое из окружающих тел. Невозможность его осуществления постулируется во втором начале термодинамики в качестве одной из эквивалентных формулировок.

Дата добавления: 2015-04-24