Эффект Комптона. Законы физики и их применение

Законы физики и их применение.

Рассказать про любой закон физики и привести примеры его проявления в природе и использования в технике

При прохождении (рассеянии) коротковолнового электромагнитного излучения (рентгеновских лучей) через вещество происходит изменение длины волны (частоты) излучении: длина волны рассеянного излучения увеличивается, а его частота – уменьшается.

Экспериментальная схема исследования эффекта Комптона:

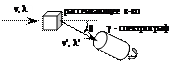По классической волновой теории света в веществе должны были бы возникать вторичные рентгеновские волны исключительно той же длины волны (частоты). Однако в экспериментах А.Комптона (1922 г.) наряду с излучением первоначальной длины волны наблюдалось рентгеновское излучение большей длины волны (меньшей частоты). При этом разность длин волн Δλ = λ' – λ оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения и направлением первичного пучка. Ни от длины волны падающего излучения λ, ни от природы рассеивающего вещества Δλ не зависела.

С точки зрения квантовой теории падающее излучение – поток квантов, и при их взаимодействии с покоящимися электронами вещества, как при упругом столкновении частиц, должны выполняться законы сохранения энергии и импульса (система «вещество – излучение» изолирована). Квант света, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение его энергии и означает увеличение длины волны λ' рассеянного излучения.

Закон сохранения энергии при эффекте Комптона имеет вид:

hν = hν' + E_{ионизации атома} + Е_{кин. электронов},

где hν и hν' – энергии падающего и рассеянного квантов, соответственно.

Очевидно, что hν > hν', т.е. ν' < ν и λ < λ'.

В релятивистском случае, закон сохранения энергии записывается в виде .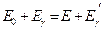

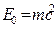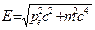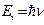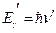Здесь – энергия электрона до столкновения; – энергия электрона после столкновения; и – энергия падающего и рассеянного квантов излучения. Энергией же ионизации атома пренебрегаем, считая электрон свободным (величина E_{ионизации} составляет единицы эВ, в то время как 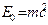для электрона ≈ 0,51 МэВ). Таким образом .

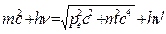Разделим равенство на с ,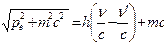

возведем в квадрат .

Для определения 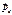воспользуемся з аконом сохранения импульса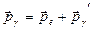

,

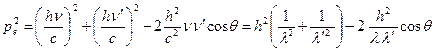
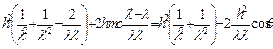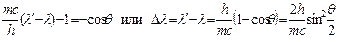
Получили формулу Комптона 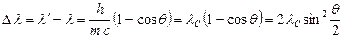, из которой следует, что увеличении длины волны при эффекте Комптона зависит только от угла рассеяния θ. Величина 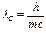получила название комптоновской длины волны, и для электрона .

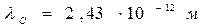1. Тепловое излучение. Гипотеза Планка. Законы ТИ.

Свечение тел, обусловленное их нагреванием, называется тепловым излучением. Тепловое излучение имеет сплошной спектр частот. Тепловое излучение единственный вид равновесного излучения. Качественной характеристикой теплового излучения называется спектральная излучательная способность (спектральная плотность энергетической светимости) – мощность излучения с единицы поверхности в единицу времени.

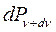- мощность излучения с единицы площади поверхности тела в интервале частот от 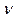до 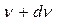. 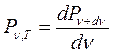- спектральная излучательная способность [В/м²]

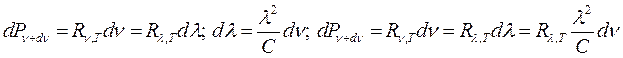
Интегральная излучательная способность:

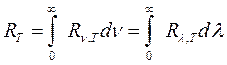
Спектральная поглощательная способность показывает, какая доля энергии за единицу времени поглощается с единицы поверхности этого тела:

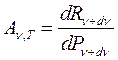
Абсолютно чёрное тело-тело способное поглощает при любой температуре всё падающее на него излучение. Поглощательная способность такого тела равна 1. Серое тело – тело, поглощательная способность которого меньше 1, но одинакова для всех частот и зависит только от температуры.

Гипотеза Планка: Атомные осцилляторы совершают излучение определёнными порциями квантами. Причём энергия кванта пропорциональна частоте колебаний: 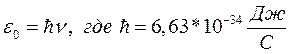Формула Планка:

1. Формула Релея-Джинса: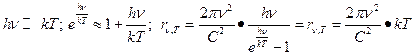

2. Закон Стефана – Больцмана: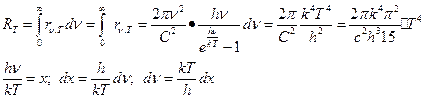

3. Закон смещения Вина: 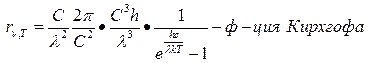. Взяв производную по 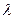и обозначив 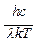=х, получим трансцендентное уравнение: 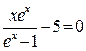, решением которого является х=4,965. Отсюда: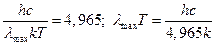

1. Корпускулярно-волновой дуализм света. Фотоны.

Дифракция, интерференция и поляризация света подтверждают волновую (электромагнитную) природу света.

Давление света может быть объяснено как волновой, так и квантовой теориями света.

Так по волновой теории света под действием электрического поля волны 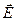электроны в веществе будут двигаться со скоростью 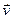в направлении, противоположном 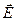. Магнитное поле 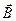волны действует на движущиеся электроны с силой Лоренца в направлении, перпендикулярном поверхности. Следовательно, электромагнитная волна оказывает на поверхность вещества давление.

Согласно квантовой теории, каждый фотон при соударении с поверхностью передает ей свой импульс. Давление света на поверхность, складывающееся из импульсов, передаваемых всеми поглощенными фотонами, оказывается пропорциональным энергетической освещенности, т.е.объемной плотности энергии. Формулы для светового давления, полученные на основе квантовой теории совпадают с аналогичными из волновой теории.

Таким образом, электромагнитное излучение обнаруживает непрерывность электромагнитной волны и дискретность световых квантов.

При увеличении частоты излучения все более сказываются квантовые (корпускулярные) свойства света.

Фотоны.

Эйнштейн развил гипотезу Планка о квантовых свойствах излучения и предположил, что квантовые свойства проявляются не только при взаимодействии света с веществом (излучение и поглощение), но и при распространении в пространстве. При этом свет ведет себя подобно совокупности некоторых частиц, энергия каждой из них определяется формулой Планка. Эти частицы в дальнейшем получили название фотонов (квантов света).

Фотоны не являются обычными частицами, распространяющимися по определенным траекториям. Это следует уже из того, что фотонам присущи такие явления, как дифракция и интерференция. Фотоны обладают не только корпускулярными, но и волновыми свойствами. Именно такая особенность фотонов и называется корпускулярно-волновым дуализмом (двойственностью).

Поскольку фотон обладает энергией E = hν = ħω, то он должен обладать и импульсом 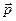. Но так как фотон движется в вакууме со скоростью света, то его энергия и импульс связаны соотношением:

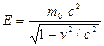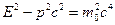, , т.е. ,

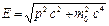где: m₀ – масса покоя фотона.

Релятивистская масса 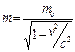при v = c должна быть бесконечно велика. Поэтому необходимо приравнять m₀ = 0, т.е. единственно возможное состояние фотона – движение с предельной скоростью, равной скорости света. Итак, если m₀ = 0, то Е = р·с.

При этом импульс фотона 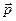направлен в сторону распространения излучения.

Корпускулярные свойства фотонов характеризуются энергией Е и импульсом 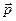, но они связаны с волновыми характеристиками: частотой ω и волновым вектором :

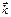E = ħω; 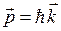или ,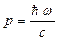

т.к. 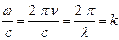– волновое число (т.е. число длин волн, укладывающихся на отрезке 2π) с размерностью [k] = 1/м.

Основные уравнения, связывающие корпускулярные свойства фотона (энергию и импульс) с волновыми свойствами (частотой и длиной волны): Е = hν и р = hν /c = h/λ.

Корпускулярные свойства фотонов проявляются, в первую очередь, при его взаимодействии с веществом.

Волновые свойства фотонов проявляются, в первую очередь, в закономерностях его распространения.

Чем больше длина волны излучения λ, тем меньше импульс и энергия фотона (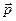, Е) и тем менее проявляются и обнаруживаются квантовые свойства. Чем меньше длина волны λ, тем больше импульс и энергия фотона (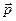, Е) и тем труднее обнаруживаются волновые свойства.

1. Волновые св-ва микрочастиц. Гипотеза де Бройля. Дифракция микрочастиц.

Микрочастица – это некий квантово-механический объект, обладающий как свойствами частицы, так и волновыми свойствами.

Первым идею о волновых свойствах частиц высказал Л. де Бройль (1924 г, Де Бройль утверждал, что не только фотоны, но и любые другие микрочастицы наряду с корпускулярными обладают также и волновыми свойствами.

Коль скоро излучение (т.е. волна) – совокупность фотонов (частиц) с энергией Е = hν и импульсом р = hν /c = h/λ, то любая микрочастица массой m и скоростью v, обладающая импульсом p = m·v = h/λ, может быть представлена в виде некоторой волны с длиной волны

λ_{де Бройля} = h/mv = h/p.

Таким образом, движение любой микрочастицы может быть описано волновым процессом, характеризуемым некоторой длиной волны λ_{деБройля}, которая была названа длиной волны де Бройля.

Волновую природу микрочастиц и формулу де Бройля убедительно подтверждают эксперименты по дифракции частиц и, в частности, электронов.

Подтверждением волновой природы микрочастиц явились опыты по дифракции электронов на поликристаллических металлических фольгах (Дж.Томпсон и П.С.Тартаковский).

Опыты состояли в прохождении пучков электронов сквозь тонкие пленки (толщиной порядка 10^{-7 м) поликристаллической структуры (}Au, Cu).

В классических опытах по дифракции рентгеновских лучей было получено, что отношение диаметра дифракционного кольца d к длине волны падающего излучения λ остается постоянным (d/λ = const) Электронные дифракционные картины возникают при условии, что длина волны де Бройля электрона λ_{деБройля} по величине приближается к постоянной кристаллической решетки (межатомному расстоянию). Убедительное подтверждение волновой природы микрочастиц было получено в экспериментах по дифракции одиночных электронов (Н.Г.Сушкин, В.А.Фабрикант, 1949 г, МГУ). В опытах использовали электронные пучки столь малой интенсивности, что можно было считать, что с тонкой металлической пленкой поочередно взаимодействуют одиночные электроны.

Свойства волн Де Бройля:

1. Волны Де Бройля – волны материи в процессе распространения могут отражаться, преломляться, интерферировать, и дифрагировать по обычным волновым законам.

2. Базовая скорость волны Де Бройля, то есть скорость, с которой перемещаются точки волны непостоянной фазой определяется соотношением 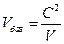, где C – скорость света, V-скорость частиц.

3. Групповая скорость волны Де Бройля (скорость переноса энергии волны или скорость перемещения точек с фиксированной амплитудой) равна скорости движения частиц. То есть волна Де Бройля перемещается вместе с частицами.

1. Волновая ф-ция: физический смысл и условия, которым она должна удовлетворять. Общее(временное) уравнение Шредингера.

Согласно гипотезе де Бройля движущейся микрочастице необходимо сопоставить процесс распространения плоской волны В случае одномерной задачи при распространении частицы в положительном направлении оси х уравнение плоской волны имеет вид: ,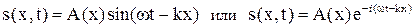

где s (x, t) – смещение точек среды c координатой х в момент времени t, k = 2π/λ – волновое число. Тогда для процесса распространения частицы по аналогии можно записать волновую функцию в виде .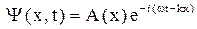

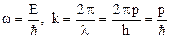. Тогда

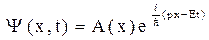.Продифференцируем это выражение по времени 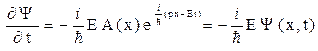.Отсюда выражая полную энергию, получим .

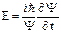Теперь дважды продифференцируем 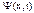по координате х и выразим импульс частицы: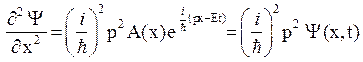

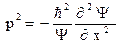
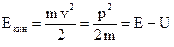. Подставляя в это выражение соотношения для полной энергии и импульса, получаем .

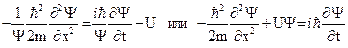В случае трехмерной задачи это выражение приобретает вид: ,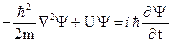

где 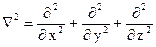– оператор Лапласа, Ψ (x, y, z, t) – волновая функция частицы, U = U(x, y, z, t) – потенциальная энергия.

Условия, которым должна удовлетворять волновая функция.

1. Так как пребывание частицы где-либо в пространстве – достоверное событие с вероят­ностью, равной единице, то для волновой функции должно выполняться условие нормировки 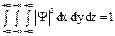. Функции Ψ и 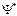, удовлетворяющие условию нормировки вероятностей, называются нормированными волновыми функциями.

2. Так как в общем случае вероятность, а значит, и интеграл 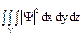, должны быть конечными величинами, подынтегральная функция 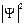, а значит, и волновая функция Ψ должна быть интегрируемой и конечной.

3. Вероятность не может изменяться скачкообразно, следовательно, волновая функция Ψ должна быть непрерывной со своими производными 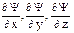, которые, безусловно, должны быть интегрируемы.

4. Поскольку вероятность должна иметь вполне определенное значение, т.е. не может быть неоднозначной величиной, волновая функция Ψ также должна быть однозначной.

5. Волновая функция Ψ должна удовлетворять одному из основных положений квантовой механики – принципу суперпозиции.

Уравнение Шредингера.

Волновые свойства частицы описываются волновой функцие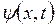й или 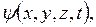которая зависит от пространственных координат и времени и удовлетворяет дифференциальному уравнению в частных производных:

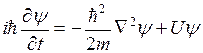(1)-Уравнение Шрёденгера

где 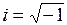, m- масса покоя частицы.

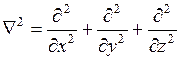- оператор Лапласа.

U(x,y,z,t) - потенциальная функция для заданного силового поля в котором движется частица

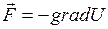
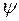- является комплексной функцией.

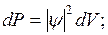
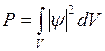(2)

Условия, которым она должна удовлетворять:

1. должна быть конечной,

2. однозначной,

3. непрерывной

4. и должны быть непрерывны и частные производные:

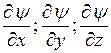
Решением этого уравнения явлвется плоская волна Де Бройля:

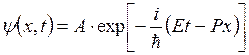
Если волновая функция имеет вид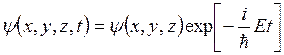

Исходя из вероятностного смысла волновой функции, вероятность Р обнаружения частицы в объёме пространства V.

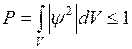
1. Волновая ф-ция: физический смысл и условия, которым она должна удовлетворять(см_6). Стационарное уравнение Шредингера.

Свободная частица – это частица, движущаяся в отсутствие внешних силовых полей. Поскольку внешние силы не действуют, потенциальная энергия U=U(x)= const (для одномерной задачи), и ее можно приравнять нулю. Следовательно, полная энергия частицы будет равна ее кинетической энергии.

Стационарное уравнение Шредингера для одномерной задачи движения свободной частицы вдоль оси х приобретает вид .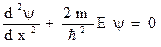

С учетом соотношений между импульсом и кинетической энергией 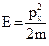и волновым числом 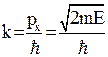уравнение можно переписать в виде .

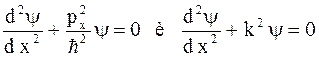Решением этого уравнения будет 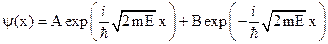или 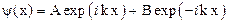, где А и В – некоторые постоянные.

Тогда полная волновая функция свободной частицы может быть определена как

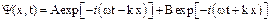или в виде .

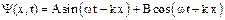Решением уравнения Шредингера для свободной частицы является суперпозиция двух плоских монохроматических волн одинаковой частоты, одна из которых распространяется в положительном направлении оси х (с амплитудой А), другая – в отрицательном направлении оси х (с амплитудой В).

Таким образом, свободная частица в квантовой механике описывается плоской монохроматической волной де Бройля. Плотность вероятности обнаружения частицы в некоторой точке пространства (рассмотрим для простоты только одну волну, распространяющуюся в положительном направлении оси х) 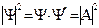не зависит от времени, т.е. все положения свободной частицы в пространстве равновероятны.

1. Принцип неопределенностей Гейзенберга.

В классической механике всякая частица в каждый момент времени имеет определённую координату. Наличие у частицы волновых свойств приводит к неопределённости в описании движения. Во избежание этого необходимо ввести квантовые поправки. Такой поправкой является соотношение неопределённостей Гейзенберга: Произведение неопределённых значений 2-х канонически сопряжённых переменных по порядку величины не может быть меньше постоянной Планка. Такими канонически сопряжёнными переменными являются координата и проекция импульса на соответствующую ось. Соотношение неопределённостей является математическим выражением принципа неопределённости: в природе не существует состояния частицы с точно определёнными значениями координаты и импульса на соответствующую ось. Это соотношение даёт теоретический предел точности измерений. Соотношение неопределённостей позволяет очертить границу применения классической механики: если неопределённость физ. величины соизмерима с самой величиной, то для описания поведения объекта применима квантовая механика. Если же неопределённость много меньше самой величины, то физическая величина является вполне определённой и для описания поведения объекта применима классическая механика. Кроме координат и проекций импульсов существуют другие пары канонически сопряжённых величин, для которых выполняется соотношение неопределённостей(например энергия и время).

Следствия:

1. Наблюдается экспериментально в атомной спектроскопии. Спектры излучения атомов не являются бесконечно узкими, так как это соответствовало бы неопределённости энергии ∆Е=0, спектральные линии имеют конечную ширину линии, которая представляет собой разброс энергии фотонов, относительно некоторого среднего значения.

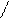
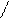
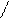
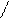
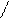
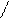
Е

По ширине спектра можно оценить время существования атомов в возбуждённом состоянии.

Г Г 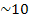^-7эВ

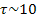^-8с

2. Вывод о невозможности состояния покоя электрочастицы.

Пусть координата частицы ограничена, тогда из соотношения неопределённостей:

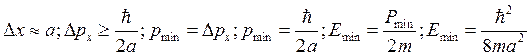
3.. В квантовой механике теряет смысл деление полной энергии частицы на кинетическую и потенциальную. И суммы этих энергий представить нельзя(по соотношению неопределённостей Гейзенберга).

1. Представление физических величин операторами. Операторы координаты, импульса, момента импульса.

Второй постулат квантовой механики:

Каждой физической величине соответствует определённый оператор этой физической величины. Соотношения между операторами в квантовой механике такие же как между соответствующими им физическими величинами в классической механике.

Оператор - математическое правило(система действий) благодаря которой можно одну функцию преобразовать в другую. В квантовой механике оператор обозначают так же как соответствующую ему физическую величину, за исключением знака ^ над величиной.

Линейный самосопряжённый оператор (хз надо ли)

Оператор 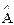соответствующей величины a.

Если для некоторых функции и 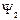и произвольных постоянных C₁ и С₂ выполняется равенство 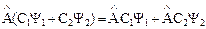, то такой оператор называется линейным. Для линейных операторов выполняется принцип суперпозиции квантовых состояний

Самосопряжённый (Эрмитов оператор) – оператор, который для 2 произвольных функций удовлетворяет условию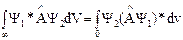

Физическим величинам соответствуют только линейные самосопряжённые операторы.

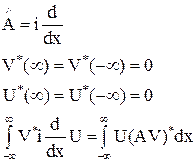
Второй постулат квантовой механики:

Каждой физической величине соответствует определённый оператор этой физической величины. Соотношения между операторами в квантовой механике такие же как между соответствующими им физическими величинами в классической механике.

Оператор - математическое правило(система действий) благодаря которой можно одну функцию преобразовать в другую.

Дата добавления: 2015-04-24