Условия возможности одновременного измерения физических величин

Важным вопросом в квантовой механике является вопрос о возможности одновременного измерения в некоторой квантовой системе значений двух физических величин, например, координат и импульса микрочастицы, двух компонент импульса и т.д.

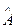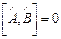Покажем, что необходимым и достаточным условием возможности одновременного точного определения двух физических величин α и β является коммутативность соответствующих им операторов и , т.е. или 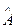· = · 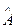. Иначе говоря, волновые функции квантового состояния, являющиеся собственными функциями операторов двух физических величин, совпадают только в случае коммутативности этих операторов. Докажем необходимость этого условия. Пусть операторы 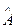и имеют общие собственные функции, т.е. соответствующие им физические величины одновременно измеримы, тогда Ψ = αΨ умножим справа на :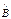

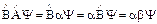
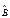Ψ = βΨ умножим справа на :

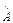Таким образом, , т.е. операторы и коммутируют.

Достаточность этого условия доказывается следующим образом. Пусть операторы 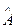и коммутируют, и пусть Ψ – собственная функция оператора . Докажем, что Ψ является также собственной функцией оператора .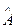

Так как Ψ – собственная функция оператора , то Ψ = βΨ.

Так как операторы 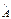и коммутируют, то .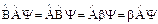

Это означает, что функция 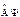так же, как и Ψ является собственной функцией оператора 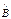, и они должны совпадать с точностью до численного множителя, т.е. 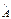Ψ = αΨ.

Но это и означает, что Ψ – собственная функция оператора .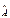

Таким образом, коммутирующие операторы, имеющие совпадающие собственные функции, соответствуют физическим величинам, которые могут быть определяемы одновременно.

1. Измерение физических величин в квантовой механике(вероятностный подход). Среднее значение физических величин.(см_11)

2.Существуют такие квантовые состояния, когда серия измерений, проведенных в одних и тех же условиях, каждый раз дает различные значения _f1, _f2 …и т.д. Тогда говорят, что физическая величина f не имеет определенного значения. В этом случае можно рассчитать вероятность P_n получения некоторого результата f_n, зная которую можно определить среднее значение величины 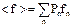и ее среднеквадратичное отклонение (дисперсию) 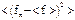. Волновая функция Ψ такого квантового состояния не является собственной функцией оператора 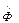, а состояние системы можно представить в виде суперпозиции собственных состояний этого оператора.

Для определения вероятности Р_n получения значения f_n воспользуемся тем, что любую волновую функцию Ψ(х) можно разложить в ряд по собственным функциям ψ_n(х) оператора 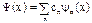, Умножим это выражение на 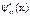и проинтегрируем по всей области изменения х.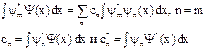

1. Стационарное уравнение Шредингера для потенциальной ямы (одномерный случай).

Свободная частица – это частица, движущаяся в отсутствие внешних силовых полей. Поскольку внешние силы не действуют, потенциальная энергия U=U(x)= const (для одномерной задачи), и ее можно приравнять нулю. Следовательно, полная энергия частицы будет равна ее кинетической энергии.

Стационарное уравнение Шредингера для одномерной задачи движения свободной частицы вдоль оси х приобретает вид .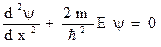

С учетом соотношений между импульсом и кинетической энергией 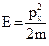и волновым числом 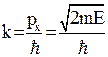уравнение можно переписать в виде .

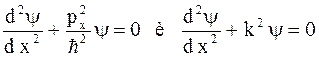Решением этого уравнения будет 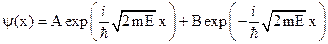или 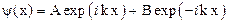, где А и В – некоторые постоянные.

Тогда полная волновая функция свободной частицы может быть определена как

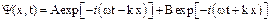или в виде .

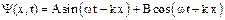Решением уравнения Шредингера для свободной частицы является суперпозиция двух плоских монохроматических волн одинаковой частоты, одна из которых распространяется в положительном направлении оси х (с амплитудой А), другая – в отрицательном направлении оси х (с амплитудой В).

Таким образом, свободная частица в квантовой механике описывается плоской монохроматической волной де Бройля. Плотность вероятности обнаружения частицы в некоторой точке пространства (рассмотрим для простоты только одну волну, распространяющуюся в положительном направлении оси х) 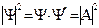не зависит от времени, т.е. все положения свободной частицы в пространстве равновероятны.

1. Стационарное уравнение Шредингера для трехмерного потенциального ящика.

U(x, y, z) = U_x(x) + U_y(y) + U_z(z),

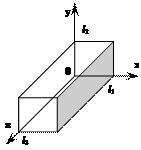где , ,

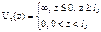
Стационарное уравнение Шредингера для такой задачи приобретает вид .

Собственные значения энергии частицы, находящейся внутри такого потенциального «ящика» могут быть записаны как , где n_х, n_у, n_z,= 1, 2 …

Таким образом, энергия частицы внутри потенциального параллелепипеда может принимать лишь строго определенные значения – 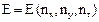, и энергетический спектр – дискретный.

В случае если потенциальный «ящик» представляет собой куб, т.е. l ₁ = l ₂= l ₃ = l, выражение для собственных значений энергии упрощается:

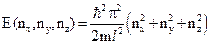, где n_х, n_у, n_z,= 1, 2 …

Уровень	Энергия	Квантовые числа	Число состояний	Степень вырожденности
		(1,1,1)		невырожденное
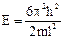
		(2,1,1) (1,2,1) (1,1,2)		вырожденное
		(1,2,2) (2,1,2) (2,2,1)		вырожденное
		(3,1,1) (1,3,1) (1,1,3)		вырожденное
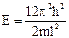
		(2,2,2)		невырожденное
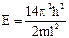
		(1,2,3) (1,3,2) (2,3,1) (3,1,2) (1,3,2) (2,3,1)		вырожденное

Состояния, при которых одному энергетическому уровню соответствуют несколько состояний, называются вырожденным, число этих состояний называется степенью или кратностью вырождения. Состояние, когда одному уровню соответствует одно состояние, называется невырожденным.

1. Стационарное уравнение Шредингера для одномерного потенциального порога.

Рассмотрим случай одномерного движения частицы в потенциальном поле, энергия которого также зависит только от координаты х, причем при х = 0 претерпевает скачок:

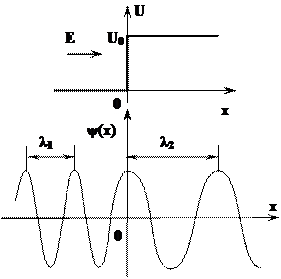
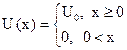
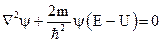для одномерной задачи движения частицы вдоль оси х приобретает вид: .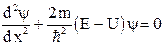

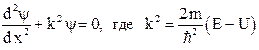1. Сначала рассмотрим случай, когда E > U₀.

Такой порог называется низким. Волны Де Бройля ведут себя подобно оптическим волнам, которые на границе 2 сред с различными показателями преломления испытывают частичное отражение.

; ; .

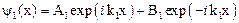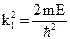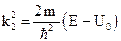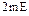
Коэффициент отражения тогда можно определить как

.

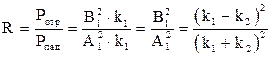Выражение для коэффициента прозрачности порога можно записать в виде:

.

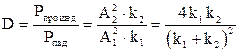R>0 следовательно даже если энергия частицы больше высоты порога есть вероятность что частица отразится от этого порога. R+D =1 значит D<1 следовательно в отличие от классической частицы вероятность проникновения квантовой частицы сквозь барьер<100%. K₁>K₂ (рисунок вверху)

2. E < U₀ - высокий порог.

k₂=ik =1

В этом случае квантовая частица, как и классическая частица, с вероятностью 100% отражается от потенциального барьера.

Определим глубину проникновения частицы за потенциальный порог l – это расстояние, на котором вероятность нахождения частицы за барьером убывает в «е» раз, т.е. 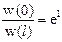или 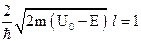. Тогда выражение для l имеет вид .

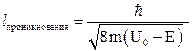1. Стационарное уравнение Шредингера для одномерного потенциального барьера.

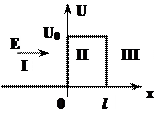
Стационарное уравнение Шрёдингера:

.

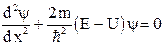Для областей I и III: 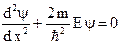или .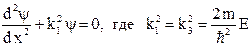

Для области II: .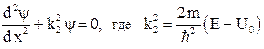

Общие решения этих уравнений будут иметь вид:

,

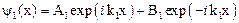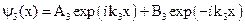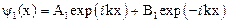
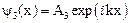. , где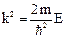

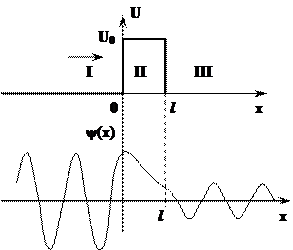
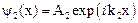.-из условия регулярности волновой функции.

, .

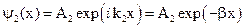Так как нет ни каких ограничений на 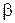то спектр значений будет непрерывным.

Коэффициенты А₁, В₁, А₂ и А₃ могут быть найдены из условий, накладываемых на волновую функцию :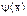

1. 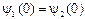и 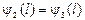– непрерывность функции ;

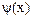2. 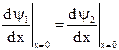и из условия непрерывности 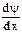в точках х = 0 и х = l.

Т.к волна Де Бройля определяет вероятность нахождения частицы или иной точке пространства оказывается что частица что частица движущаяся в области 1 в направлении оси х имеет отличную от 0 вероятность попадания в область 3. Энергия и импульс не меняются. Такое явление называется туннельный эффект. Туннельный эффект характеризуется вероятностью проникновения через барьер, эта вероятность характеризуется коэффициентом прозрачности потенциального барьера D.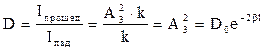

.

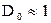
Экспериментальные подтверждения:

1.Авто-электронная эмиссия. 2.Автоионизация. 3.Альфа-распад радиоактивных ядер.

Применение: Сканирующий туннельный микроскоп(Создан в 1982 году)

1. нет
2. нет
3. Спектр атома водорода. Ширина спектральных линий.

Спектр излучения атома водорода

Серия Лаймана – это переходы на уровень : ,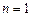

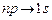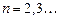
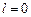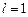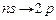Серия Бальмера –это переходы на уровни с ( и ): , , с уровней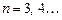

Серия Пашена – это переходы на уровни с 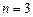и т.д.

Квантовая теория позволяет полностью описать поведение атома водорода, в том числе и интенсивность линий в спектре излучения.

1. Ядерная модель атома. Постулаты Бора.

1. Квантовая модель атома. Волновые функции и квантовые числа.

Рассмотрим систему, состоящую из неподвижного ядра с положительным зарядом 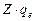и одного электрона, вращающегося вокруг ядра. Потенциальная энергия взаимодействия между ними .

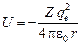Стационарное уравнение Шредингера 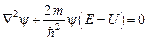для рассматриваемой задачи можно записать как 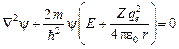или в сферических координатах

.

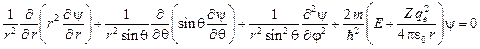Для решения дифференциальных уравнений такого типа используется метод разделения переменных, т.е. полною волновую функцию представим в виде 2 частей: радиальной и угловой.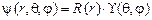

Умножим обе части уравнения на 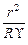и проведем разделение переменных, тогда

Так как левая часть зависит только от радиуса, а правая от угловой функции, то левая и правая части равны постоянной разделения. Пусть эта постоянная равна , где l – целые числа. Итак, для левой части уравнения получаем

.

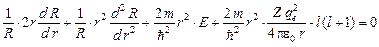Умножим на 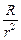и введём безразмерные величины: ; ;

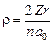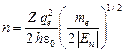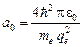
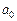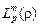Здесь – первый Боровский радиус. Тогда решение последнего получается в виде: , где –полиномы Лагерра. (n=1,2,3… l=0,1,2,3…,n-1).

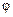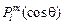Угловая часть волновой функции также ищется с помощью разделения переменных ( и ) и имеет вид , где – полиномы Лежандра( Полная координатная часть волновой функции, являющейся решением уравнения Шредингера, имеет вид .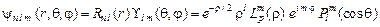

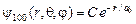- волновая функция в основном состоянии водорода.

Постоянная определяется из условия нормировки вероятности на единицу: .

.

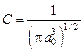
Тогда нормированная волновая функция .

1. Моменты электрона. Эффект Зеемана.

Моменты импульса электронов и атомов, определяемые по классической электронной теории.

1. Механический орбитальный момент импульса 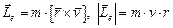, где m, v – масса и скорость электрона. При этом вектор 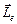перпендикулярен орбите электрона.

2. Магнитный орбитальный момент 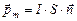, , 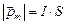где I – электронный ток, S – площадь орбиты электрона. Определим 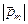: , , здесь е – заряд электрона, T – период обращения электрона по орбите.

Тогда . Следует учесть, что также перпендикулярен орбите электрона, но вектора 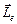и направлены в противоположные стороны. Механический и магнитный орбитальные моменты электрона связаны выражением .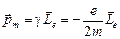

Здесь 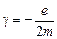– гиромагнитное (или магнито–механическое) отношение орбитальных моментов электрона.

3. Орбитальный механический момент импульса атома по классической электронной теории равен геометрической (векторной) сумме орбитальных моментов всех электронов атома: 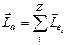, Z – число электронов атома.

4. Орбитальный магнитный момент импульса атома по классической электронной теории равен геометрической (векторной) сумме магнитных моментов всех электронов атома: 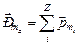. Очевидно, что сохраняется соотношение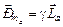

Теперь рассмотрим электронные и атомные моменты с точки зрения квантовой механики. Хронологически первыми экспериментами по изучению магнитных моментов электронов в атоме, проявляющихся в магнитном поле, были опыты П.Зеемана (1896г). Явление расщепления спектральных линий, а, следовательно, и энергетических уровней, переходы между которыми обеспечивают излучение, во внешнем магнитном поле получило название эффекта Зеемана. Различают нормальный и аномальный эффекты Зеемана.

Нормальный эффект Зеемана наблюдается в сильных магнитных полях.

При помещении источника излучения с частотой 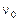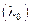в магнитное поле, направленное параллельно направлению распространения излучения, наблюдается излучение с двумя симметричными относительно начальной 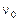частотами: и . И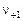злучение с начальной частотой 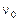при этом исчезает:

.

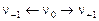Если исследуемое излучение распространяется перпендикулярно вектору магнитного поля, то излучение с частотой 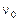симметрично расщепляется на три компоненты: , 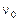и .

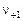Аномальный эффект Зеемана наблюдается в слабых магнитных полях и заключается в расщеплении каждой спектральной линии излучения на множество компонент.

При этом внешнее магнитное поле считается слабым, если взаимодействие между орбитальным 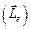и магнитным 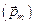моментами электрона в атоме сильнее, чем взаимодействие каждого из этих моментов 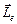или с внешним магнитным полем. Поэтому именно аномальный эффект Зеемана выявляет взаимодействие между собственными внутренними моментами электрона в атоме. С увеличением напряженности магнитного поля 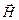взаимодействие между внутренними моментами электрона становится все менее существенным по сравнению с их взаимодействием с внешним магнитным полем. Расщепление спектральных линий при этом усиливается, соседние линии постепенно начинают сливаться, и остается 2 или 3 частоты излучения в зависимости от взаимного направления магнитного поля 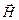и излучения.

1. Моменты электрона(см_22). Опыты Шредингера-Герлаха.

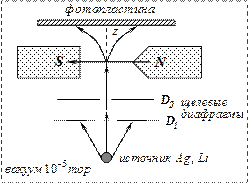
Идея опытов Штерна – Герлаха состояла в определении силы, которая может быть определена как 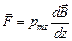. Для электрона в s –состоянии орбитальное квантовое число 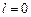, следовательно, механический момент импульса 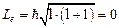и магнитный момент 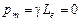, а значит и моменты атома с одним s –электроном на внешней оболочке также должны равняться нулю. Внешнее магнитное поле никак не должно влиять на движение пучка таких атомов. Ожидалось, что распределение атомов будет непрерывно симметричным с максимумом интенсивности в центре. Однако в экспериментах наблюдалось расщепление пучка атомов на два приблизительно равных по интенсивности пучка. По известной величине неоднородности магнитного поля и установленной по отклонению атомов силе 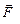было определено, что проекция этого магнитного момента 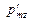на направление магнитного поля для элементов I-ой группы оказалась численно равной магнетону Бора: .

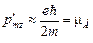1. Спин-орбитальное взаимодействие.

С. Гаудсмитом и Дж. Уленбеком (1925 г.) была высказана гипотеза о том, что кроме орбитального момента импульса 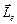и соответствующего ему магнитного момента электрон обладает собственным, не связанным с движением в пространстве, механическим моментом импульса 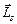– спином и соответствующим ему спиновым магнитным моментом .

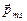Спин электрона (и других микрочастиц) – это внутреннее неотъемлемое свойство частиц (подобно массе, заряду и т.п.). Но при этом спин – исключительно квантовое понятие, не имеющее классического аналога.

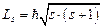, - Спиновый момент, где s – спиновое квантовое число.

Спиновый механический момент электрона: .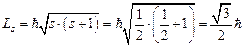

Проекция спинового момента импульса на направление магнитного поля квантуется подобно проекции орбитального момента

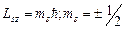-магнитное квантовое число.

Спиновые механический и магнитный моменты 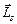и 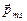так же, направлены противоположно относительно друг друга.

Таким образом, для полного описания состояния электрона в атоме необходимо использовать четыре квантовых числа:

главное n 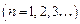,орбитальное l 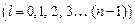,магнитное m ,

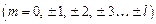магнитное спиновое m_S .

Механическим моментам импульса электрона соответствуют магнитные моменты которые взаимодействуют между собой. Это взаимодействие называется спин–орбитальным.

Величина полного момента импульса электрона 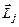определяется внутренним квантовым числом j: 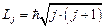, где 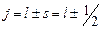, l – орбитальное квантовое число, s – спиновое квантовое число.

Существует правило отбора для внутреннего квантового числа j: .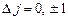

1. нет
2. Спонтанное и индуцированное излучение. Коэффициенты Эйнштейна.

1. Лазеры: принцип устройства, основные типы и области применения. Свойства лазерного излучения.
2. Квантовые системы тождественных частиц. Фермионы и бозоны.

1. Квантовое статическое распределение Ферми-Дирака. Плотность квантовых состояний.

Квантовая статистика Ферми – Дирака справедлива для частиц обладающих полуцелым спином и подчиняющихся принципу Паули. Её исходными положениями являются дискретность энергетических уровней и неразличимость частиц. Рассмотрим идеальный Ферми – газ(систему из не взаимодействующих Ферминов).

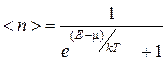- Распределение Ферми – частиц по энергиям. Средние числа заполнения квантовых состояний с энергией E.

Следствия:

1. <n> - не может быть больше 1, так как это вероятность заполнения состояния с энергией Е при температуре t.

2. Химический потенциал Ферми частиц больше 1.

3. При любых энергиях средние числа заполнения не превышают 1, что соответствует принципу Паули. В случае разряженного газа для описания поведения квантовых частиц можно использовать классическое распределение Максвелла – Больцмана.

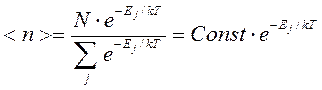
4. Поскольку химический потенциал имеет размерность энергии, то в случае Ферми частиц его называют энергией Ферми, а соответствующий энергетический уровень уровнем Ферми.

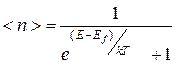
5. Помимо энергии Ферми вводится импульс Ферми и скорость Ферми.

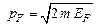-Импульс Ферми.

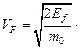- Скорость Ферми.

Физический смысл распределения Ферми.

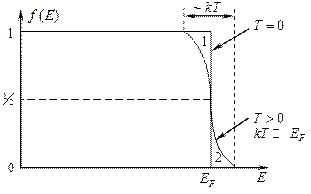
Энергия Ферми – максимальная энергия которой могут обладать Ферми частицы при Т=0. При повашении Т происходит размытие ступеньки. При Т отличной от 0 вероятность заполнения равняется 0,5.

Плотность числа квантовых состояний (или энергетическая плотность состояний) – это число разрешенных энергетических состояний, приходящихся на единичный интервал энергии.

Пусть N – число частиц (состояний) с энергией Е, а dN – число состояний с энергией в интервале от Е до Е + dE. Тогда плотность числа состояний определяется как

,

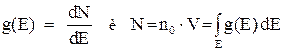где n₀ – концентрация частиц, V – объем, занимаемый системой частиц. Воспользуемся выражением для энергии Ферми для определения концентрации частиц с некоторой энергией Е:

.

Множитель 2 учитывает двукратное вырождение состояний для выполнения принципа Паули для фермионов. После подстановки n₀(E) в выражение для g(E)

и дифференцирования, получаем

или через энергию Ферми .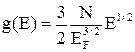

Таким образом, плотность квантовых состояний g(E) оказывается пропорциональной ~ Е^1/2.

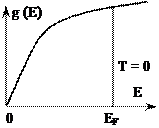По определению энергетической плотности состояний площадь под графиком зависимости g(E) устанавливает полное число возможных энергетических состояний, а значит, и полное число частиц N.

Полная энергия системы частиц при данной температуре Т может быть определена через функцию распределения f(E, Т) и плотность энергетических состояний g(E) по формуле: .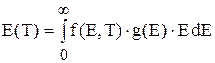

1. Квантовое статическое распределение Бозе-Эйнштейна. Фотоны и фононы.

Отличительной особенностью равновесной системы бозонов по сравнению с системой фермионов является равенство нулю энергии Ферми: E_F = 0. Таким образом, функция распределения Бозе – Эйнштейна приобретает вид: 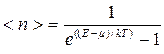.-распределение Бозе - частиц по энергиям.

Бозе-конденсация - скопление большого числа частиц с энергией равной 0. Проявляется в сверхтекучести и сверхпроводимости. В случае низких температур или высоких давлений единственно приемлемой для описания базонов является статистика Бозе - Эйнштейна.

Дата добавления: 2015-04-24