
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операторы физических величин
|
|
|
|
1. Оператор координаты. Действие этого оператора сводится к умножению волновой функции на эту координату:  Ψ = х·Ψ,
Ψ = х·Ψ, 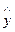 Ψ = у·Ψ,
Ψ = у·Ψ,  Ψ = z·Ψ или
Ψ = z·Ψ или  = х,
= х, 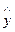 = у,
= у,  = z.
= z.
2. Операторы проекций импульса. Действие этих операторов сводится к дифференцированию по соответствующим координатам с некоторым множителем, равным 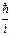 :
:  Векторный оператор ипмульса:
Векторный оператор ипмульса: 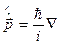 , где
, где 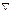 – векторный оператор градиента – «набла»:
– векторный оператор градиента – «набла»:
 .
.
3. Оператор квадрата импульса. Для построения этого оператора воспользуемся очевидным соотношением классической механики:  .
.
 или, используя оператор Лапласа
или, используя оператор Лапласа
 .
.
4. Оператор момента импульса. Согласно классической формуле для момента импульса 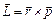 и тогда в проекциях вектора
и тогда в проекциях вектора  на оси координат
на оси координат
Lx = ypz – zpy, Ly= zpx– xpz, Lz = xpy – ypx
Обобщая эти выражения на операторы соответствующих физических величин, получаем
 ,
, 
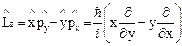 , Тогда оператор квадрата момента импульса можно записать так
, Тогда оператор квадрата момента импульса можно записать так  .
.
- Представление физических величин операторами(см_9). Операторы потенциальной, кинетической и полной энергии.
5. Оператор кинетической энергии.  .
. 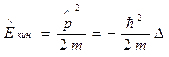 .
.
6. Оператор потенциальной энергии. Этот оператор представляет собой оператор умножения волновой функции на функцию U(x, y, z), определяющую потенциальную энергию частицы в стационарном силовом поле 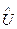 Ψ = U·Ψ.
Ψ = U·Ψ.
7. Оператор полной энергии. сумма операторов кинетической и потенциальной энергий  - Гомильтониан.
- Гомильтониан.
- Измерение физических величин в квантовой механике(вероятностный подход). Условия одновременного измерения нескольких величин.
Рассмотрим процесс определения некоторого физического параметра квантовой системы в серии одинаковых опытов. Возможны два случая:
1. Для некоторых квантовых состояний системы измерение физической величины f в ряде опытов дают каждый раз один и тот же результат. В этом случае говорят об определенном значении физической величины f в данном квантовом состоянии, которое называют собственным состоянием оператора 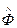 , соответствующего измеряемой величине f.
, соответствующего измеряемой величине f.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 591; Нарушение авторских прав?; Мы поможем в написании вашей работы!