
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальное уравнение гармонического колебания как математическая модель
|
|
|
|
Задача о колебаниях пружинного маятника
Тело массой м совершает вдоль прямой горизонтальные колебания под действиемпружины. Исследуйте характер движения этого тела, пренебрегая массой пружины, трением и сопротивлением среды.
Решение: Ось х направим вдоль прямой колебаний, а начало координат помести в точке равновесия.
Тогда положение тела, моделируемого материальной точкой, определяется его абсцисой х, которая зависит от времени. т.е. является функцией t:x=(t). Нужно найти эту функцию и по ней исследовать характер колебаний.
По закону Гука сила натяжения пружины пропорциональна ее удлинению. В нашем случае проекция силы на ось х равна F=-kx, где коэффициент пропорциональности k>0, а знак минус поставлен потому, что сила упругости пружины направлена от тела к началу координат (к положению равновесия). По второму закону Ньютона имеем дифференциальное уравнение:
m²(t)= -kx или
x²(t)=-w2x, (1)
где w2=  . Теперь интересующие нас выводы будем получать из решения этого уравнения, а не из непосредственного, например, экспериментального исследования самого физического процесса. Именно это уравнение математически выражает общие законы (Ньютона и Гука) и условия рассматриваемого колебательного процесса и потому называется его математической моделью.
. Теперь интересующие нас выводы будем получать из решения этого уравнения, а не из непосредственного, например, экспериментального исследования самого физического процесса. Именно это уравнение математически выражает общие законы (Ньютона и Гука) и условия рассматриваемого колебательного процесса и потому называется его математической моделью.
Приведем решение уравнения (1), основанное на физических представлениях. Для этого проведем окружность радиуса r с центром в начале координат (рисунок) и рассмотрим равномерное движение точки М по этой окружности с угловой скоростью w>0, квадрат которой равен  , тогда модуль центростремительного ускорения этой точки будет a =
, тогда модуль центростремительного ускорения этой точки будет a = 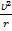 или, с учетом того, что
или, с учетом того, что 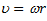 получим
получим 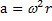
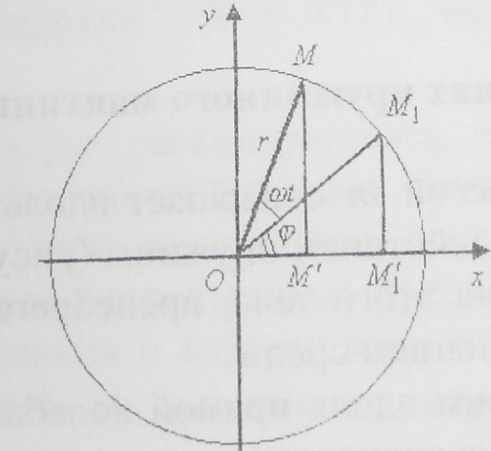
Рисунок – равномерное движение точки М по окружности
Так как центростремительное ускорение направлено по радиусу окружности к ее центру, последнее равенство в векторной форме примет вид
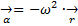
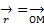 – вектор, направленный от центра и, имеющий длину r. Учитывая, что проекция ускорения на ось х есть вторая производная от абсциссы времени, получим дифференциальное уравнение второго порядка
– вектор, направленный от центра и, имеющий длину r. Учитывая, что проекция ускорения на ось х есть вторая производная от абсциссы времени, получим дифференциальное уравнение второго порядка
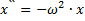
решение, которого может быть истолковано как зависящая от времени абсцисса точки М при ее равномерном движении по окружности против хода часовой стрелки. Найдем эту зависимость.
Пусть при t=t0 точка М совпадает с М1 (рисунок), тогда в момент времени t радиус Ом будет составлять угол 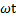 с ОМ1 и угол (
с ОМ1 и угол (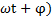 с осью х, поэтому абсцисса точки М как функция
с осью х, поэтому абсцисса точки М как функция 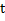 будет равна:
будет равна:
х=r cos ( 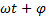 ) (2)
) (2)
Итак, модели 1 и 2 равносильны. Но первая описывается дифференциальным уравнением, а вторая – конечным. Отметим, что колебания материальной точки на пружине, движение проекции точки М на диаметр при равномерном ее движении по окружности, малые колебания математического маятника, колебания тока в электрической цепи и многие колебательные процессы другой природы с соответственно подобранными параметрами и начальными условиями будут иметь одну и ту же математическую модель.
«Поэтому, изучив математическую модель, мы можем часто делать выводы о свойствах разнообразных объектов. Кроме того, если различные объекты имеет одинаковую математическую модель, то становиться возможным моделировать один из этих объектов другим. Например, вместо исследования колебаний сложной линейной механической системы можно производить измерения в соответственно подобранной электрической цепи, имеющей ту же математическую модель. На этом основано действие электромеханических, оптико-механических и других аналоговых устройств. Замечательно, что при применении таких устройств сама математическая модель как бы остается в стороне (значение интересующих нас механических величин непосредственно получаются по результатам электрических измерений), хотя именно на единстве модели основана возможность этого применения»
9) 2 – КАНОНИЧЕСКАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Название «математическое программирование» связано с тем, что целью решения задач, рассматриваемых в этой дисциплине, является математически обоснованный выбор программы действий (не путать с программированием – составлением программы для ЭВМ).
В математическое программирование обычно включаются задачи на максимум и минимум с ограничениями типа равенств или неравенств.
К линейному программированию относятся те задачи математического программирования, в которых и целевая функция, и ограничения линейны.
Из линейного программирования рассмотрим задачу об использовании ресурсов.
Предприятие может осуществлять производство трех видов товара 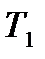 ,
, 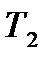 ,
, 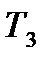 из двух видов сырья
из двух видов сырья 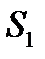 и
и 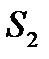 . Нормы расхода на производство товаров вместе с данными о ценах и запасах представлены в таблице 1, где
. Нормы расхода на производство товаров вместе с данными о ценах и запасах представлены в таблице 1, где 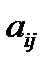 – количество сырья
– количество сырья 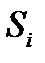 , которое расходуется на производство единицы товара
, которое расходуется на производство единицы товара 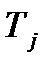 ,
, 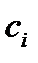 – стоимость единицы товара
– стоимость единицы товара 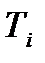 . Требуется построить математическую модель для определения плана выпуска товаров
. Требуется построить математическую модель для определения плана выпуска товаров  ,
, 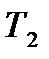 ,
, 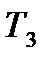 в количествах
в количествах 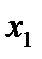 ,
, 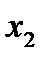 ,
, 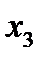 , при которых выручка от их реализации (продажи) была бы максимальной.
, при которых выручка от их реализации (продажи) была бы максимальной.
Математическая модель:
Найти значения 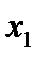 ,
, 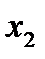 ,
, 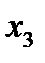 , которые доставляют
, которые доставляют 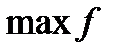 , где
, где 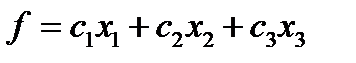 ,
,
при условиях 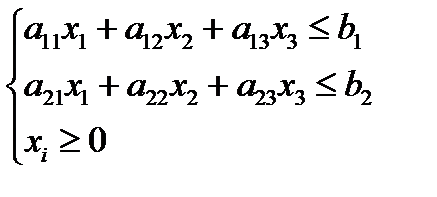 .
.
Этой системе неравенств должна удовлетворять совокупность всех вариантов производства, обеспеченных имеющимися ресурсами. (Задача линейного программирования, в которой ограничения на запасы записаны в виде неравенств).
Таблица 1
| Виды товаров Виды сырья |
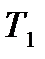
|
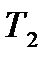
|
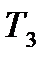
| Запасы |
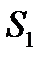
| 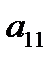
| 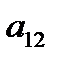
| 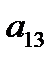
| 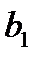
|
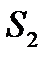
| 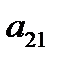
| 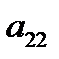
| 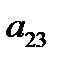
| 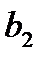
|
| Цена единицы товара | 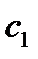
| 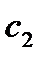
| 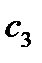
|
Теперь построим математическую модель транспортной задачи:
стоимость перевозки 1 т груза из пункта отправления 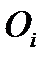 в каждый пункт назначения
в каждый пункт назначения 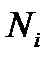 задана таблицей 2.
задана таблицей 2.
Таблица 2
| Пункты назначения Пункты отправления | 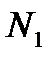
| 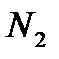
| 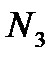
| Запасы |
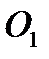
| 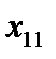
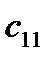
| 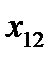
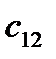
| 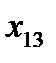
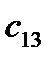 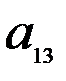
| 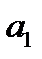
|
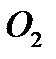
| 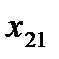
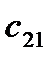
| 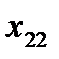
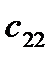
| 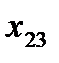
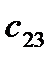
| 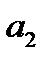
|
| Потребность в грузе | 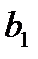
| 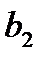
| 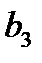
|
Здесь 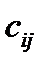 – стоимость перевозки 1 т груза из пункта отправления
– стоимость перевозки 1 т груза из пункта отправления 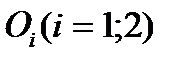 в пункт назначения
в пункт назначения 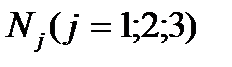 . Весь груз из пунктов отправления нужно перевезти в пункты назначения, поэтому
. Весь груз из пунктов отправления нужно перевезти в пункты назначения, поэтому 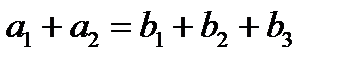 .
.
Составить математическую модель для определения оптимального плана перевозки грузов так, чтобы общая стоимость транспортных расходов была бы наименьшей.
Обозначим через 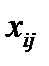 – количество груза, предназначенного к отправлению из
– количество груза, предназначенного к отправлению из 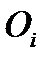 в
в 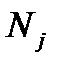 , тогда придем к следующей математической модели:
, тогда придем к следующей математической модели:
Найти значения 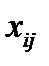 , которые доставляют
, которые доставляют 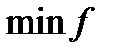 , где
, где 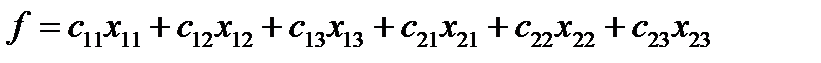 ,
,
при условиях:
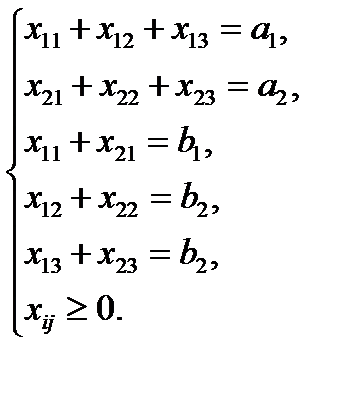
(Каноническая задача линейного программирования, в которой ограничения на запасы и потребности записаны в виде уравнений).
10) 1 – УСТОЙЧИВОСТЬ РЕШЕНИЙ
Устойчивость решения – очень важный практический вопрос.
Исходные данные – приближенны. При использовании ЭВМ возникают ошибки округления. Каким же образом погрешности влияют на результат?
Если малые изменения входных данных мало влияют на результат – решение устойчивое.
В противном случае таким решением пользоваться нельзя.
Пример:
X + 10*Y = 11
10X + 101*Y=111
X=1; Y=1;
Если же
X + 10*Y = 11,1
10X + 101*Y=111
X=11,1; Y=0;
Система плохо обусловлена, а решение неустойчивое.
Другой пример:
X + 2*Y = 39
-X + 3*Y=21
X=15; Y=12;
Если же
X + 2*Y = 39,1
-X + 3*Y=21
X=15,06; Y=12,02; - устойчивое решение.
В первом случае неустойчивость решения показывает нам необходимость технической доработки.
Устойчивые решения можно использовать на практике, неустойчивые решения показывают необходимость корректировки модели с помощью технических специалистов в проблеме.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1713; Нарушение авторских прав?; Мы поможем в написании вашей работы!