Механическая модель СВ

Для лучшего понимания свойств случайных величин, как дискретных так и непрерывных или смешанных, полезной является механическая модель, имитирующая такое распределение единичной массы на числовой оси, при котором масса любого ее интервала численно равна вероятности попадания СВ Х в этот интервал. В частности, если СВ Х – дискретная, то она моделируется системой материальных точек, абсциссы которых совпадают со значениями СВ, а массы с их вероятностями. Очевидно, в механической модели математическое ожидание СВ Х совпадает с абсциссой центра масс соответствующего распределения, дисперсия – с центральным моментом инерции, а плотности вероятности f(x) соответствует плотность распределения массы. В случае непрерывной CВ Х вероятность ее попадания в интервал, как и соответствующая масса, выражается определенным интегралом

P (a<X <b)= 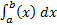, а математическое ожидание, как и абсцисса центра масс:

М(Х)=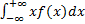

В заключении построим ММ задачи и решим ее:

Два охотника А и В одновременно выстрелили в медведя, который был убит, и в его шкуре обнаружена только одна пробоина. Шкуру продали за 42 $. Как по справедливости разделить эту сумму между А и В, если вероятности их попадания таковы:

Р (А)=0,8, Р(В)=0,4?

Ясно, что вырученные деньги несправедливо поделить в отношении 0,8:0,4=2:1, так как при том же отношении Р(А):Р(В)=1:0,5=2:1, где Р(А)=1 и Р(В)=0,5, все деньги должен получить охотник А. При построении модели следует учесть, что пробоина в шкуре одна.

Событием, что А и В попали в одно и тоже место мы пренебрегаем, как маловероятным и в модели считаем, что в медведя попал только один из них. Так как они стреляли независимо друг от друга, то в соответствии с принципом независимости 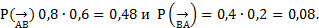Именно пропорциональности этим вероятностям, т.е в отношении 0,48:0,08=6:1и надо по справедливости разделить 42 $. Между А и В Тогда точка В получит 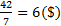, а А в шесть раз больше, т.е. 36 .

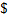8) 1. УСЛОВИЯ ВОЗНИКНОВЕНИЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Нормальное распределение, одно из важнейших распределений вероятностей. Термин " Нормальное распределение " применяют как по отношению к распределениям вероятностей случайных величин, так и по отношению к совместным распределениям вероятностей нескольких случайных величин (т. е. к распредслениям случайных векторов).
Распределение вероятностей случайной величины Х называется нормальным, если оно имеет плотность вероятности
. (*)
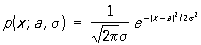Семейство Нормальное распределение (*) зависит, т. о., от двух параметров а и s. При этом математическое ожидание Х равно а, дисперсия Х равна s². Кривая Нормальное распределение у = р (х; а, s) симметрична относительно ординаты, проходящей через точку х = а, и имеет в этой точке единственный максимум, равный 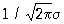. С уменьшением s кривая Нормальное распределение становится все более и более островершинной (см. рис.). Изменение а при постоянном s не меняет форму кривой, а вызывает лишь ее смещение по оси абсцисс. Площадь, заключенная под кривой Нормальное распределение, всегда равна единице. При a = 0, s = 1 соответствуюшая функция распределения равна
.
В общем случае функция распределения Нормальное распределение (*) (х; а, s) может быть вычислена по формуле (x; а, s) = Ф (t), где t = (х — а)/s. Для функции Ф (t) (и нескольких ее производных) составлены обширные таблицы. Для Нормальное распределение вероятность неравенства 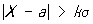, равная 1— Ф (k)+ Ф (— k), убывает весьма быстро с ростом k (см. таблицу).

kk	Вероятность<
	0,31731
	0,04550
	0,00269
	0,00006

Во многих практических вопросах при рассмотрении Нормальное распределение пренебрегают поэтому возможностью отклонений от а, превышающих 3s, — т. н. правило трех сигма (соответствующая вероятность, как видно из таблицы, меньше 0,003). Вероятное отклонение для Нормальное распределение равно 0,67449s.

Нормальное распределение встречается в большом числе приложений. Издавна известны попытки объяснения этого обстоятельства. Теоретическое обоснование исключительной роли Нормальное распределение дают предельные теоремы теории вероятностей (см. также Лапласа теорема, Ляпунова теорема). Качественно соответствующий результат может быть объяснен следующим образом: Нормальное распределение служит хорошим приближением каждый раз, когда рассматриваемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой.

Нормальное распределение может появляться также как точное решение некоторых задач (в рамках принятой математической модели явления). Так обстоит дело в теории случайных процессов (в одной из основных моделей броуновского движения). Классические примеры возникновения Нормальное распределение как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. Максвеллу (закон распределения скоростей молекул).
Совместное распределение нескольких случайных величин X ₁, X ₂,..., X _s называется нормальным (многомерным нормальным), если соответствующая плотность вероятности имеет вид: 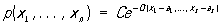, где ,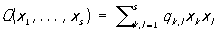
q_{k, l} = q_{l, k} — положительно определенная квадратичная форма. Постоянная С определяется из того условия, что интеграл от р по всему пространству равен 1. Параметры a₁,..., a_s равны математическим ожиданиям X₁,..., X_s соответственно, а коэффициент q_{k, l} могут быть выражены через дисперсии s ₁ ²,..., s _s ² этих величин и коэффициент корреляции s _{k, l} между X_k и X_l. Общее количество параметров, задающих Нормальное распределение, равно (s + 1)(s + 2)/2 – 1 и быстро растет с ростом s (оно равно 2 при s = 1, 20 при s = 5 и 65 при s = 10). Многомерное Нормальное распределение служит основной моделью статистического анализа многомерного. Оно используется также в теории случайных процессов (где рассматривают также Нормальное распределение в бесконечномерных пространствах)

Дата добавления: 2015-04-24