Применения метода к решению невероятностных задач

1) Найти 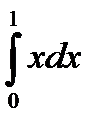, исходя из вероятностных представлений. Решение:

Рассмотрим интеграл вида: 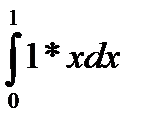(18.1)

явно выделив в качестве множителя в подынтегральном выраже­нии единицу, которая будет играть роль плотности распределения:

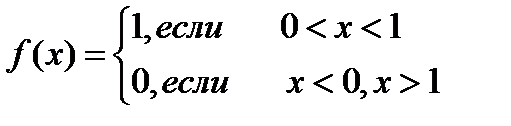
Но тогда выражение (18.1) будет математическим ожиданием случайной величины х, равномерно распределенной в интерва­ле(0,1):

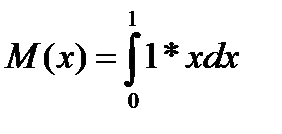
Математическое ожидание можно оценить средним арифме­тическим наблюдаемых значений случайной величины:

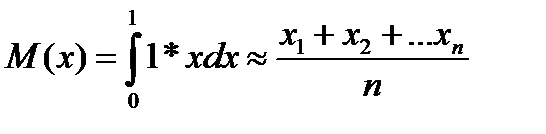
Возьмем n=16 (малая выборка) и воспользуемся телефон­ным справочником для получения случайных чисел (берем по­следние цифры). Так как у нас интервал (0,l), то удовлетворять этому условию будут числа: 0,0; 0,1; 0,2;...; 0,9.

Итак, просматривая последние цифры 16 номеров телефонов, выпишем их последовательность, например, полученную в нашем эксперименте: 6; 9; 3; 1; 5; 3; 8; 4; 7; 6: 0; 2; 4; 7; 8; 9.

Так как каждое случайное число должно принадлежать интер­валу (0,1), то

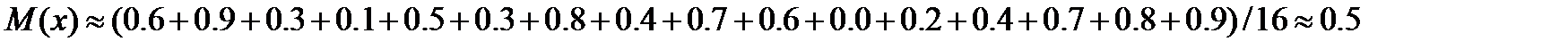
(Ответ записан с точностью до одной значащей цифры)

Точное значение этого интеграла равно 0,5, так как

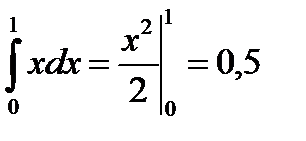
2) Исходя из вероятностных представлений, вычислить число .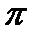

Рассмотрим квадрат со стороной, равной единице, и четверть круга в нем (рисунок 18.2). Тогда геометрическая вероятность по­падания случайной величины в четверть круга, площадь которого

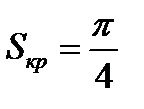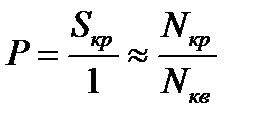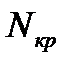будет , где и 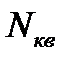- число случайных точек попадания в четверть круга и в квадрат соответст­венно. Отсюда 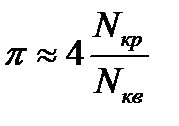. Как и при решении предыдущей задачи для определения 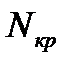и 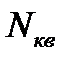используем те же случайные числа, объединив их в пары:

(0,6; 0,9), (0,3; 0,1), (0,5; 0,3), (0,8; 0,4), (0.7; 0,6), (0; 0,2), (0,4; 0,7), (0,8; 0,9).

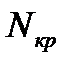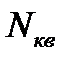В нашем эксперименте =6, =8.

Следовательно,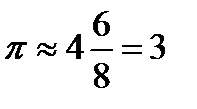

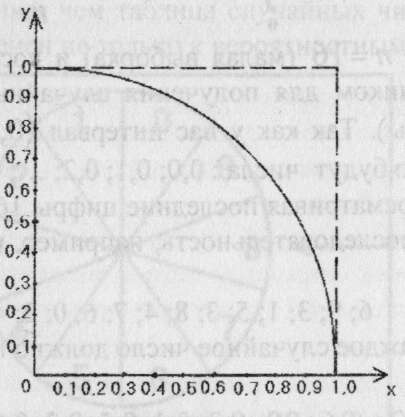
Рисунок 18.2 - Пояснение к экспериментальному определению числа .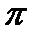

Дата добавления: 2015-04-24