Латиноамериканская модель глобального развития

В 1974 г. группа аргентинских учёных во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью глобального развития. Предпосылки для выполнения работы при обсуждении модели “Мир-3” послужил тезис о том, что основные преграды на пути гармонического развития человечества заключаещися главным образом в неравномерном распределении богатства между различными странами.

В модели Эрреры за основную цель развития человеческого общества принято достижение удовлетворительных условий жизни всеми странами мира, а не просто рост материального потребления. Под удовлетворительными условиями понимаются некоторые достаточно высокие уровни медицинского обслуживания, образования, обеспеченности питанием и жильём.

4.2 МЕТОД УСРЕДНЕНИЯ И ЕГО ПРИЛОЖЕНИЕ К РЕШЕНИЮ ПЕРЕОПРЕДЕЛЁННЫХ СИСТЕМ

Кажется, что еще можно сказать о системе линейных алгебраических уравнений, когда известно множество методов ее решения. И всё же …. Если решать задачу, линейная модель которой описывает некоторую реальную ситуацию, то здесь могут встретиться различные осложнения, хотя бы потому, что коэффициенты системы, включая и правые части, получают с помощью измерений и по этой причине они являются приближенными числами. Для повышения их точности стремятся сделать как можно больше измерений. Но именно это приводит к переопределенной системе уравнений, не имеющей решения в классическом смысле. Однако подобные задачи выдвигаются практикой и потому необходимо иметь такие их математические модели, которые позволяют получать неклассические, обобщенные решения.

требуется как можно лучше оценить «истинное значение» некоторой величины х, для чего проводятся n прямых измерений, результаты которых представлены несовместной системой уравнений

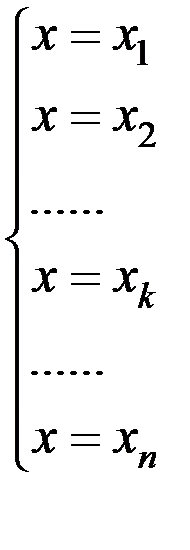, (5.1)

где 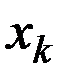результат 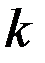-го измерения.

Используя всю имеющуюся экспериментальную информацию, сложим почленно уравнения системы, тогда получим

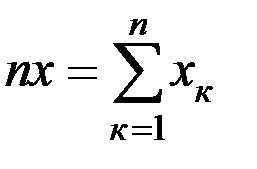, т.е. 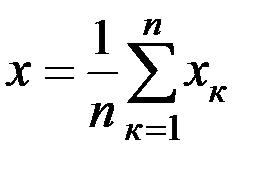. (5.2)

Укажем практическую оценку среднего арифметического (5.2) по числу значащих цифр. Самый простой способ состоит в сравнении среднего арифметического с результатами отдельных измерений. Среднее значение округляют, сохраняя слева все цифры, остающиеся неизменными или почти неизменными во всех отдельных измерениях, а все остальные отбрасываются. Рассмотрим пример: пусть неизвестная величина измерена пять раз [44, с. 385]: х₁ = 4,781; х₂ = 4,795; х₃ = 4,769; х₄ = 4,792; х₅ = 4,779, среднее арифметическое которых равно 4,7832. Возникает вопрос: какие цифры найденного среднего следует сохранить?

Цифра 4 целых в среднем арифметическом значении и во всех результатах отдельных измерений совпадает и должна быть сохранена, как надёжная. То же самое относится и к цифре 7, находящейся в разряде десятых. Цифра 8 в разряде сотых среднего арифметического незначительно отличается от цифр сотых отдельных измерений и сохраняется как значащая. Остальные отбрасываются. Итак, ответ с точностью до трёх значащих цифр: х = 4,78.

Система линейных алгебраических уравнений может оказаться несовместной с точки зрения классической математики и тогда, когда существует, например, решение такой реальной задачи:

энергетический и коксующийся уголь добывают на трех участках шахты, причем средние затраты на 1 тонну его и процентное распределение добычи дано в таблице 5.1.

Номер участка	Энергетический уголь в %	Коксующийся уголь в %	Затраты на одну тонну
			9,5 ден.ед.
			11 ден.ед.
			13 ден.ед.

Оцените объективно обусловленные стоимости одной тонны энергетического и одной тонны коксующегося угля.

Обозначим через 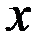и 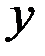стоимости 1т соответственно энергетического и коксующегося угля, тогда на основании данных таблицы получим систему уравнений:

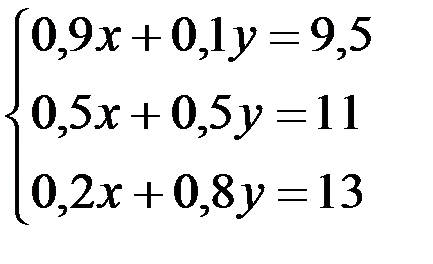(5.3)

Решая совместно два первых уравнения этой системы найдем: х = 9,1, y= 12,9, а, подставив эти значения в третье уравнение придём к противоречию. Это означает, что система трех уравнений с двумя неизвестными несовместна, однако, учитывая возможность погрешностей в числовых данных и существование экономически обусловленных цен как 1т энергетического, так и 1т коксующегося угля, будем искать способ определения этих цен. Для того, чтобы они лучше учитывали фактические затраты на угледобычу в данных условиях, нужно использовать всю информацию, которая содержится в системе (5.3). Если, как в случае системы (5.1), сложить почленно все уравнения системы (5.3), то получим одно уравнение с двумя неизвестными, а их нужно два, причём таких, при которых система будет иметь в классическом смысле единственное решение. Проще всего поступить так: сложить почленно первые два уравнения системы (5.3) и сохранить третье, тогда придём к системе:

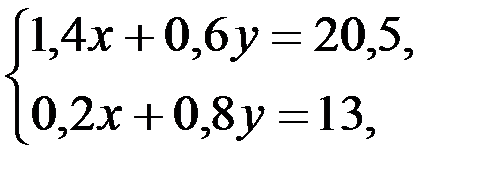
решая которую, находим: х = 9, у = 14. Отметим, что существует афоризм: чистая математика делает то, что можно, так, как нужно, а прикладная наоборот: то, что нужно – так, как можно, а с практической точки зрения – даже и так, как нужно.

4) 2. МЕТОД УСРЕДНЕНИЯ И ЕГО ПРИЛОЖЕНИЯ К РЕШЕНИЮ ПЕРЕОПРЕДЕЛЕННЫХ СИСТЕМ

ПЕРЕОПРЕДЕЛЕННАЯ СИСТЕМА - система, число уравнений к-рой больше числа неизвестных. В линейном случае такие системы задаются прямоугольной 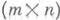-матрицей, m<n, где m - число уравнений, а п - число неизвестных. Для П. с. первоочередным является вопрос ее разрешимости, выражаемый в условиях совместности.

Напр., П. с. линейных алгебраич. уравнений

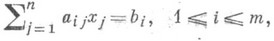
разрешима тогда и только тогда, когда ранги основной матрицы 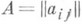и расширенной матрицы, полученной приписыванием к Астолбца свободных членов, совпадают.

Для П. с. линейных дифференциальных уравнений с постоянными коэффициентами

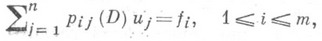(1)

где P_ij - многочлен от одного (обыкновенное уравнение) или нескольких (уравнение с частными производными) переменных, a D - символ дифференцирования, условие совместности выражается в виде однородной системы уравнений с постоянными коэффициентами

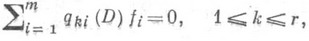(2)

где матрица q находится по матрице р с помощью алгебраич. соображений,

Для П. с. (1) дифференциальных уравнений с частными производными с переменными коэффициентами

P_ij=P_ij (x, D).отыскание условий совместности, имеющих вид (2) с 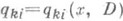, является значительно более трудной задачей.

Простейшим примером П. с. служит система дифференциальных уравнений

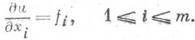
Условия совместности для этой системы, необходимые и достаточные для ее разрешимости, имеют вид

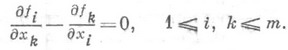
Аналитич. функции многих комплексных переменных можно также рассматривать как решения П. с. уравнений

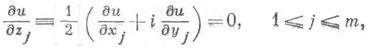
где

Дата добавления: 2015-04-24